基于小波變換的改進軟閾值圖像去噪算法
李曉飛,邱曉暉
(南京郵電大學 通信與信息工程學院,江蘇 南京 210003)
基于小波變換的改進軟閾值圖像去噪算法
李曉飛,邱曉暉
(南京郵電大學 通信與信息工程學院,江蘇 南京 210003)
由于經典的小波閾值函數存在一定的缺陷,如硬閾值函數在閾值處不具有連續性,軟閾值函數的小波估計系數和原系數之間存在著恒定的偏差,會導致去噪后的圖像出現失真、產生吉布斯震蕩等問題。文中綜合典型的小波閾值函數的優點,并綜合一些改進的方法,針對其缺點,提出了一種改進的閾值函數。該函數不僅在閾值處是連續的、小波估計的系數漸進原系數,并且具有可微性,易于實現梯度算法的自適應學習。為了驗證該閾值函數的優越性,通過仿真實驗對幾種小波去噪方法的均方差(MSE)和峰值信噪比(PSNR)進行了對比。實驗結果表明,用改進后的閾值函數進行去噪,無論是在視覺效果上,還是在均方差和峰值信噪比性能分析上均優于常用的閾值函數。
小波變換;圖像去噪;小波閾值去噪;閾值函數;高斯噪聲;均方差;峰值信噪比
0 引 言
圖像在傳輸或者提取的時候,會受到各種各樣噪聲的污染,因此,會影響圖像的質量和對圖像的后續處理。故圖像去噪是圖像處理過程中一個必不可少的步驟。小波變換能同時在時頻域中對信號進行分析,利用它進行圖像去噪是小波變換的重要應用領域之一。1994年,DonohoDL和JohnstoneIM在小波變換的基礎上提出了小波閾值去噪算法,在目前應用廣泛[1-2]。但是由于典型的軟、硬閾值函數都有相應的缺陷,硬閾值函數在閾值處不連續,而軟閾值函數中估計的小波系數和帶有噪聲的小波系數之間存在著一個恒定的偏差,從而限制了小波閾值的進一步應用。文獻[3-5]分別提出了三種不同的改進算法,這些改進算法也可以對典型軟、硬閾值函數的缺點進行一定的改善,但是效果并不是很明顯。
因而,文中結合經典的軟、硬閾值函數的特點以及文獻[3-5]中各閾值函數的優缺點,提出了一種更好的閾值函數。該函數不僅在閾值處連續、小波估計系數漸進原系數,并且易于計算。
1 小波閾值去噪的基本原理
小波變換具有比較好的數據去相關性,它可以使大部分能量集中在少量較大的小波系數上,而噪聲的能量分布在整個小波域,對應著大量的較小的小波系數;即在小波域,有效信號對應的系數很大,而噪聲對應的系數很小[6-8]。故可以選取合適的閾值對小波系數進行截斷處理,將絕對值小于閾值的小波系數都置為零,而將大于閾值的小波系數保留或者予以適當收縮,得到估計后的小波系數,然后對估計的小波系數進行重構,最后可以得到去噪后的信號[9]。
小波閾值去噪過程可以分為3步:
第一步:對噪聲圖像進行小波變換,選擇合適的小波基和小波分解層數,將含噪圖像進行小波分解,得到相應的小波分解系數;
第二步:根據設定的閾值和閾值函數對信號進行去噪處理;
第三步:對處理過的小波系數進行小波逆變換,得到去噪后的估計信號。
1.1 小波閾值函數
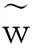
(1)硬閾值函數:保留大于閾值的系數,把小于閾值的系數都置為零。
該閾值函數的表達式為:
(2)軟閾值函數:把大于閾值的系數減去閾值的大小,把小于閾值的系數置零,表達式為:
軟閾值函數去噪后得到的小波系數的整體連續性較好,但它的缺陷是,當系數超過設定的閾值后,小波系數的估計值和原系數之間有恒定的偏差,這將直接影響重構的信號與真實信號的逼近程度;硬閾值函數去噪雖然在均方誤差意義上比軟閾值函數要有優勢,但是它在閾值處不連續,得到的估計信號會產生一定的附加震蕩,光滑性不是很理想[11]。
1.2 改進的閾值函數
針對典型的軟、硬閾值函數的缺點,文獻[3-5]分別提出了不同的閾值函數,它們都在一定程度上改善了軟、硬閾值函數的缺點,對含噪圖像的處理都有一定的效果。文中根據經典的軟、硬閾值函數和文獻[3-5]的啟發構造了一種新的閾值函數:
改進的小波閾值函數的數學分析如下:
(1)連續性分析。



(2)漸進性分析。
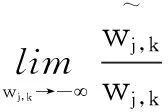
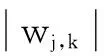
2 仿真實驗及結果分析

圖1為friendgray的仿真實驗圖。
為了更好地驗證文中提出的新閾值函數的去噪效果,下面用均方差(MeanSquaredError,MSE)和峰值信噪比(PeakSignal-to-NoiseRatio,PSNR)進行圖像去噪后的效果分析。MSE的值越小,說明圖像的質量越好,而PSNR的值越大,說明圖像的質量越好[13]。定義式分別為:

圖1 friendgray的仿真實驗圖
PSNR=10×lg(2552/MSE)

通過仿真實驗得到的實驗數據如表1所示。

表1 降噪后各圖像的MSE和PSNR對比
通過表1的數據可知,改進閾值函數的去噪效果比傳統的軟、硬閾值及文獻[3-5]中改進的閾值函數的去噪效果好。
3 結束語
文中綜合典型的小波閾值函數的優點,并結合一些改進的方法,提出了一種改進的閾值函數。通過仿真實驗對幾種小波去噪方法的MSE和PSNR進行了對比。結果表明,用該函數進行去噪,無論是在視覺效果上,還是在均方差和峰值信噪比性能分析上均優于常用的閾值函數。
[1]DonohoDL.Adaptingtounknownsmoothnessviawaveletshrinkage[J].JournalofAmericanStatisticalAssociation,1995,90:1200-1224.
[2]DonohoDL.De-noisingbysoft-thresholding[J].IEEETransonIT,1995,41(3):613-627.
[3] 王 蓓,張根耀,李 智,等.基于新閾值函數的小波閾值去噪算法[J].計算機應用,2014,34(5):1499-1502.
[4]CuiHuimin,ZhaoRuimei,HouYanli.Improvedthresholddenoisingmethodbasedonwavelettransform[C]//Procofinternationalconferenceonmedicalphysicsandbiomedicalengineering.[s.l.]:[s.n.],2012:1354-1359.
[5]LingDC,SamsudinA,AbduliahR.Aestheticmeasuresforassessinggraphicscreens[J].JournalofInformationScienceandEngineering,2000,16:97-116.
[6] 張 平,高義中.工業設計的色彩量化處理[J].南京理工大學學報:自然科學版,1998,22(5):407-411.
[7] 葉重元,黃永東.小波閾值去噪算法的新改進[J].計算機工程與應用,2011,47(12):141-145.
[8] 王 可,余隋懷,樂萬德,等.面向計算機輔助工業設計的色彩設計系統[J].計算機輔助設計與圖形學學報,2004,16(10):1425-1429.
[9]ChangSG,YuB,VetterliM.Adaptivewaveletthresholdingforimagedenoisingandcompression[J].IEEETransactionsonImageProcessing,2000,9(9):1532-1546.
[10] 劉成云,陳振學,馬于濤.自適應閾值的小波圖像去噪[J].光電工程,2007,34(6):77-81.
[11] 吳芳平,狄紅衛.基于Curvelet變換的軟硬閾值折衷圖像去噪[J].光學技術,2007,33(5):688-690.
[12]BruceAG,GaoHongye.Waveshrinkandsemisoftshrinkage[J].StatisticsSinica,1997,7(4):855-874.
[13] 邢丹俊,王繼成.基于提升小波的自適應閾值圖像去噪[J].計算機技術與發展,2008,18(2):42-45.
AnImprovedSoft-thresholdImageDenoisingAlgorithmBasedonWaveletTransform
LIXiao-fei,QIUXiao-hui
(CollegeofCommunicationandInformationEngineering,NanjingUniversityofPostsandTelecommunications,Nanjing210003,China)
Astheclassicalwaveletthresholdingfunctionhascertaindefects,forexample,thehardthresholdfunctionisnotcontinuousatthethreshold,andthereisconstantdeviationbetweentheoriginalcoefficientforsoft-thresholdfunction,whichcancauseimagedistortionafterdenoisingandproducetheproblemsuchasGibbsphenomena.Animprovedthresholdfunctionbasedontheadvantagesofthetypicalwaveletthresholdingfunctionandcombinedsomeimprovedmethodsisproposed.Thefunctionisnotonlycontinuousatthethreshold,theestimatedwaveletcoefficientsapproachingtheoriginalcoefficient,butalsodifferentialandeasytorealizetheadaptivelearningofgradientalgorithm.Inordertoverifythesuperiorityofthethresholdingfunction,throughthesimulationexperiment,theMeanSquareError(MSE)andPeakSignal-To-NoiseRatio(PSNR)fromseveralwaveletdenoisingmethodsarecompared.Accordingtotheexperimentalresults,thisproposedmethodhasbetterinvisualeffectandperformanceanalysisforMSEandPSNRthanthetraditionalthresholdfunctions.
wavelettransform;imagedenoising;waveletthresholddenoising;thresholdfunction;Gaussiannoise;MSE;PSNR
2015-07-03
2015-10-15
時間:2016-03-22
江蘇省自然科學基金(BK2011789);東南大學毫米波國家重點實驗室開放課題(K201318)
李曉飛(1989-),女,碩士研究生,通信作者,研究方向為智能信號處理、數字圖像處理;邱曉暉,教授,研究方向為現代信號中的智能信號處理。
http://www.cnki.net/kcms/detail/61.1450.TP.20160322.1519.050.html
TP
A
1673-629X(2016)05-0076-03
10.3969/j.issn.1673-629X.2016.05.016

