基于CS和LS-SVM的入侵檢測算法
陳天宇,吳 凡,馬世杰,李 雷
(南京郵電大學,江蘇 南京 210023)
基于CS和LS-SVM的入侵檢測算法
陳天宇,吳 凡,馬世杰,李 雷
(南京郵電大學,江蘇 南京 210023)
由于入侵檢測中具有原始數據量大、維度較高、冗余度較大等特點,導致傳統的入侵檢測算法面對海量數據時檢測識別度低,運行時間長,性能較差。為此,文中提出了一種將壓縮感知和最小二乘支持向量機應用于入侵檢測系統的方法。其創新點主要在于:引入壓縮采樣技術提取原始數據特征,在保留原數據主要特征的前提下,將高維數據轉化為低維數據;利用最小二乘支持向量機直接在觀測域中訓練和分類數據,且核函數通過組合核函數構建。仿真結果表明,運用壓縮感知進行特征提取能夠極大保留原始特征,而最小二乘支持向量機能夠在不損失精度的前提下加速分類。該方法能夠較大地減少訓練時間,并可以有效提高檢測精度。
壓縮感知;最小二乘法;支持向量機;入侵檢測
1 概 述
隨著經濟社會的發展,互聯網被廣泛應用于社會的各行各業。然而,人們在享受互聯網帶來的便利和高效的同時,其本身卻充斥著安全隱患,對財產安全和隱私造成了巨大威脅。在這樣的社會大環境下,入侵檢測系統(IntrusionDetectionSystem,IDS)成為當下的熱門研究領域[1],其本質上是個分類問題[2]。目前,入侵檢測主要通過機器學習、數據挖掘、神經網絡等方式完成[3-8],其一般流程為提取入侵行為或正常行為的數據特征,構建出一個特征數據庫,從中進行模式匹配,從而完成入侵檢測。然而,一方面,隨著網絡技術的發展,寬帶不斷提高,受限于奈奎斯特采樣定理,實時采樣對軟硬件的要求不斷提高;另一方面,采用機器學習的方法進行入侵檢測時,必然會面對樣本數據相關性大、維數高,訓練重復樣本多,訓練時間過長并且入侵樣本標記困難等問題[2]。
近年來,由D.Donoho等在矩陣分析、統計理論、優化理論等研究的基礎上,提出了一種新的信息采樣理論—壓縮感知理論(CompressedSensing,CS)[9-12]。該理論指出,若信號在某個變換域內是稀疏的,則該信號就可以用一個與變換基不相關的觀測矩陣實現從高維到低維的映射,并可以將低維信號重構,從而恢復出完整的信息。
在壓縮感知理論中,基于l0范數最小化的重構算法是NP-hard問題,即使將問題轉化為l1范數最小化問題,計算復雜度仍為O(N3)[13],其中N為信號長度。
上述算法都無法避免對信號進行重構,同時傳統的基于壓縮感知的入侵檢測在低信噪比下檢測效果不佳。
支持向量機[14](SupportVectorMachine,SVM)以統計學為基礎,通過尋求結構風險最小化來實現經驗風險和置信范圍的最小化,廣泛應用于統計分類中,適用于線性可分以及線性不可分的問題,在較小的訓練樣本時也能獲得良好的分類效果。
基于以上原因,文中將原始入侵檢測數據進行預處理后,選取合適的觀測矩陣和稀疏基進行壓縮采樣并歸一化,進而將觀測域下的低維數據通過最小二乘支持向量機建立檢測分類器,完成入侵檢測。在最小二乘支持向量機中,采用組合核函數的形式,尋求獲得最近似實際的分類模型。仿真結果表明,與經典的機器學習方法和壓縮感知算法相比,文中提出的算法可以有效改善支持向量的稀疏性,提高系統的魯棒性,檢測性能大幅提高,且利用組合核函數實現的分類結果較一般核函數的分類結果更精確。
2 壓縮感知和支持向量機理論
2.1 壓縮感知

(1)

式(1)表明,S,X其實表示的是同一個信號,只不過S為信號在Φ域中的表現形式,X為其在時域中的表現形式。在Φ域中,假設X的加權系數列S中有K個非零系數,則X可以用這K個非零系數來表示,稱信號X的稀疏度為K。當K?N時,就稱信號X具有稀疏性。

y=ψX=ψΦS=ΘS
(2)
其中:ψ為觀測矩陣;Θ=ψΦ是一個M×N維的壓縮傳感矩陣。
由于ψ是事先選定的確定矩陣,不隨信號X變化,因此該測量過程具有非自適應性。
綜上所述,壓縮感知理論共包括如下三方面:
第一,對于信號X,找到其稀疏正交基Φ,使得該信號在Φ上稀疏表示。
第二,找到一個M×N的測量矩陣ψ,使其與Φ滿足非相關性,即在對信號X進行壓縮和降維的過程中,基本不損失原信號X中的重要信息,該概念等價于Θ滿足約束等距條件[15](RestrictedIsometryProperty,RIP),也就是說,對?s∈RN,有
(3)
其中,ε為失真因子。
第三,提取原信號X中的特征信息后,采取適當的重構算法和分類算法,恢復數據信息并進行檢測。
2.2 支持向量機
支持向量機是一種強大的機器學習工具,已經在模式識別、數據挖掘等方面廣泛應用。由于壓縮感知技術在重構時采用的算法復雜度較高,而Calderbank等證明了利用SVM將觀測域上的壓縮信號直接分類,其性能與對原信號直接使用SVM的精度類似[16],故文中采用將觀測域下的信號直接利用SVM對數據進行訓練和分類。
假設樣本集為:(xi,yi),i=1,2,…,n,x∈Rd,y∈{-1,1}是類別標號。在一個d維的空間中,在處理非線性問題時,先尋找某個非線性映射Π:Rd→H,x→π(x),將原空間Rd中的數據x映射到一個高維特征空間中,接著通過引入某種符合Mercer條件的核函數K(xi,xj),使支持向量機可以在高維核空間中直接利用線性函數進行線性分類。那么在高維空間中所用的分類函數如下所示:
(4)
其中:ai>0是Lagrange因子;b是域值。
目前使用率最高的核函數有如下三種:
(1)多項式核函數(Poly)。
K(x,xi)=[(x·xi)+l]q
(5)
(2)Gauss徑向基核函數(RBF)。
K(x,xi)=exp(-‖x-xi‖2/σ2)
(6)
(3)Sigmoid核函數(Sigmoid)。
K(x,xi)=tanh[v(x×xi)+c]
(7)
其中,v>0,c<0。
為使分類性能最佳,文中采用改進交叉驗證[17]的方法尋找最優參數。
3 基于壓縮感知和支持向量機的入侵檢測算法
3.1 稀疏基和隨機觀測矩陣的選取
基于對入侵檢測數據的認識,文中的稀疏基采用Gabor緊框架字典[18],其概念為:設a和b是給定的正數,對于?g∈L2:L2(R),稱函數族。
ψj,k(x):=ei2πkbxg(x-ja),j,k∈Z
(8)
為經過函數g得到的Gabor函數系。
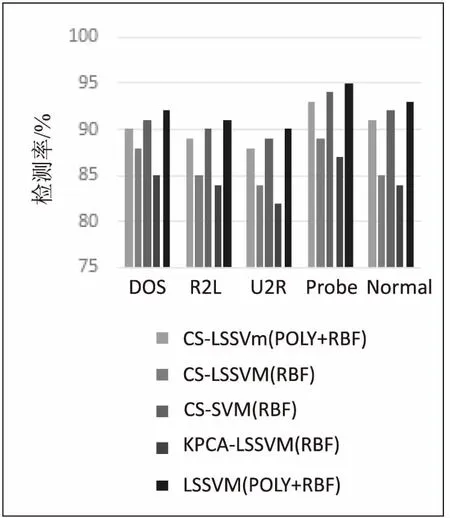
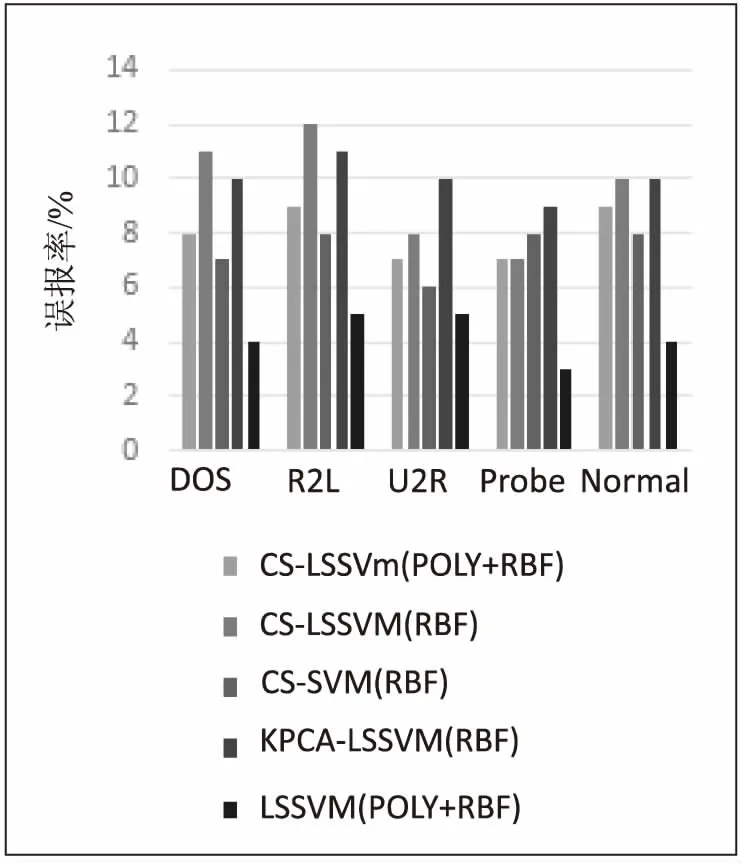
若存在常數A和B(0 (9) 則稱函數族(見式(8))是L2的一個Gabor框架,并且稱A和B為框架界。而‖·‖和<·>表示L2的范數和內積,當式(9)中A和B相等時稱對應的框架為緊框架。 文中采用的觀測矩陣為伯努利隨機矩陣,其定義為: 對于矩陣Φ∈RM×N,矩陣中每個獨立且同分布的元素都服從伯努利分布,即: (10) 伯努利矩陣具有較強的隨機性,因此符合RIP要求。 3.2 支持向量機的選取 文中采用最小二乘支持向量機(LS-SVM)的方法。LS-SVM是普通支持向量機的一種擴展,將最小二乘線性誤差的平方和取作損失函數,從而求解一系列方程組。LS-SVM收斂速度快,計算速度得到提升,因而在非線性分類和模式識別中得到廣泛應用。 Π為非線性映射,則最小二乘支持向量機的優化問題可以描述為: (11) 其中:w為權值向量;γ為正則化系數;ek為實際值與真實值的誤差。 約束條件為: yk[ωTp(xk)+b]=1-ekk=1,2,…,N 另一方面,文中選用Poly+RBF構成組合核函數,其形式為: K(x,xi)=α[(x·xi)+l]q+(1-α)× exp(-‖x-xi‖2/σ2) (12) 式中,權系數α(0≤α≤1)作用是調節兩種核函數在作用時的權重。 當求出優化問題的解ai之后,組合核函數LS-SVM模型的決策超平面可表示為: (13) 3.3 系統建立及算法描述 文中的入侵檢測系統共包含5個模塊,具體如圖1所示。 圖1 入侵檢測系統模塊 具體實現步驟表述為: Step1:數據預處理。將原始數據向量化表示。 Step2:文中采用隨機伯努利矩陣作為測量矩陣,采用Gabor緊框架字典作為稀疏正交基。此時測量矩陣和稀疏基滿足RIP條件,且利用它們構成的壓縮傳感矩陣能夠有效地完成對原始數據的特征提取,得到低維向量。 Step3:將得到的特征數據歸一化到[0,1]的區間內,避免特別大的數據在數據集中起主導作用,提高計算精度。歸一化操作如下式: yi'=(yi-min)/(max-min) (14) Step4:使用最小二乘支持向量機分類。作為對照,并分別選取RBF核函數和POLY+RBF組合核函數。 Step5:運用K折交叉驗證(K-CV)的方法選擇最優參數。將數據集平均分成10組,接著輪流將當中9組作為訓練集,其中1組作為驗證集(或叫測試集),進行10次實驗。依據每次實驗的分類精度,來確定針對該數據集的最優參數。 Step6:利用最優參數對數據進行訓練和預測,得出最優分類器和分類結果。 4.1 實驗平臺 實驗所用平臺為:IntelCorei5,CPU2.4GHz,4GBRAM,Windows8.1操作系統,Matlab2014a。 4.2 數據來源 為分析比較實驗結果,文中采用KDDCUP99入侵檢測數據集,對分別采用不同的特征提取策略,不同的支持向量機,以及不同核函數的情況下得到的入侵檢測算法效率進行比較分析。KDD99數據集總共由500萬條記錄組成,文中攻擊數據采用KDDCUP99中特征比較顯著的四大類網絡攻擊: (1)DenialOfService(DOS); (2)RemotetoLocal(R2L); (3)UsertoRoot(U2R); (4)Surveillanceorprobe(Pride)。 由于數據量過大,文中只采用部分數據進行仿真實驗,如表1所示。 表1 仿真實驗用的樣本數據 4.3 對比算法和性能指標 為使文中的CS-LSSVM算法檢測結果更具說服力,引入KPCA-LSSVM,CS-SVM,LSSVM進行對比試驗,并引入如下四個檢測性能指標: 運行時間t。 4.4 結果與分析 圖2~4展示了以KDDCPU99為實驗數據,在五種算法中進行入侵檢測的DR、FDR和LDR。通過對比,進一步研究了基于壓縮感知的入侵檢測下具備的優勢和不足。 圖2 不同算法的檢測率 圖3 不同算法的漏報率 圖4 不同算法的誤報率 對圖2~圖4進行分析,可得到如下結論: (1)在CS-SVM算法中,使用POLY+RBF構成的組合核的性能指標明顯優于單一核,可見組合核更能充分劃分出數據的特性。 (2)CS-LSSVM的性能指標明顯優于KPCA-LSSVM。這表明就特征提取的策略而言,在本問題中,運用CS的效果優于KPCA。 (3)CS-LSSVM的性能指標稍遜色于CS-SVM。這是運用了最小二乘理論,犧牲分類精度換取收斂速度所導致的必然結果;然而,CS-LSSVM的精確度足以滿足一般要求。 (4)CS-LSSVM的性能指標與采用普通LSSVM的性能指標相接近。這說明文中采用的稀疏基和觀測矩陣是合適的,能夠充分提取原始數據的特征。 五種算法的運行時間如圖5所示。 圖5 訓練與檢測時間 由圖5可知,采用CS-LSSVM算法,運行時間比KPCA-LSSVM更快,且遠少于其他算法。這是由于運用壓縮采樣進行特征提取,極大地降低了數據維度,提高了數據稀疏性導致支持向量維度降低,樣本的訓練和分類速度快。結果表明了文中CS-LSSVM的巨大優勢和運用價值。 文中提出了一種基于壓縮感知并結合運用最小二乘支持向量機的入侵檢測算法。該方法的創新點在于:通過選擇恰當的稀疏基和觀測矩陣,有效對網絡數據壓縮采樣。特別在網絡數據獲取階段,直接使用特征提取后的數據,用組合核LSSVM構建的分類器進行訓練和入侵檢測。仿真實驗的結果表明,該方法與傳統方法在DR、FDR和LDR上較為接近,但運行時間遠優于傳統的非壓縮方法。另一方面,采用組合核函數構建的LSSVM在分類精度上明顯優于單一的核函數。未來,還將進一步研究如何提高檢測精度,以及在已經正確分類的前提下如何對壓縮后的數據進行重構等問題。 [1]PerezFM,Mora-GimenoF,Marcos-JorqueraD,etal.Networkintrusiondetectionsystemembeddedonasmartsensor[J].IEEETransactionsonIndustrialElectronics,2011,58(3):722-732. [2]HofmannA,SickB.Onlineintrusionalertaggregationwithgenerativedatastreammodeling[J].IEEETransactionsonDependableandSecureComputing,2011,8(2):282-294. [3]PandaM,AbrahamA,PatraMR.Ahybridintelligentapproachfornetworkintrusiondetection[J].ProcediaEngineering,2012,30:1-9. [4]YusufovnaSF.Integratingintrusiondetectionsystemanddatamining[C]//Procof2008internationalsymposiumonubiquitousmultimediacomputing.[s.l.]:[s.n.],2008:256-259. [5]YiYang,WuJiansheng,XuWei.IncrementalSVMbasedonreservedsetfornetworkintrusiondetection[J].ExpertSystemswithApplications,2011,38(6):7698-7707. [6] 陳桂林,王生光,徐靜妹,等.基于GA和組合核的SVM入侵檢測算法[J].計算機技術與發展,2015,25(2):148-151. [7] 張 拓,王建平.基于CQPSO-LSSVM的網絡入侵檢測模型[J].計算機工程與應用,2015,51(2):113-116. [8] 黃 亮,吳 帥,譚國律,等.基于EPSO-RVM的網絡入侵檢測模型[J].計算機工程與應用,2015,51(3):85-88. [9]DonohoDL.Compressedsensing[J].IEEETransactionsonInformationTheory,2006,52(4):1289-1306. [10]CandesEJ,RombergJ,TaoT.Robustuncertaintyprinciples:exactsignalreconstructionfromhighlyincompletefrequencyinformation[J].IEEETransactionsonInformationTheory,2006,52(2):489-509. [11] 戴瓊海,付長軍,季向陽.壓縮感知研究[J].計算機學報,2011,34(3):425-434. [12] 焦李成,楊淑媛,劉 芳,等.壓縮感知回顧與展望[J].電子學報,2011,39(7):1651-1662. [13]DonohoD,TannerJ.Observeduniversalityofphasetransitionsinhigh-dimensionalgeometry,withimplicationsformoderndataanalysisandsignalprocessing[J].PhilosophicalTransactionsofTheRoyalSocietyAMathematicalPhysicalandEngineeringSciences,2009,367(1906):4273-4293. [14] 郭麗娟,孫世宇,段修生.支持向量機及核函數研究[J].科學技術與工程,2008,8(2):487-490. [15]ZhangT.SparserecoverywithorthogonalmatchingpursuitunderRIP[J].IEEETransactionsonInformationTheory,2011,57(9):6215-6221. [16]TyS,AllenJD,LiuX.Detectionofmodifiedmatrixencodingusingmachinelearningandcompressedsensing[J].ProcofSPIE,2011,8063(13):1216-1217. [17] 鄧 蕊,馬永軍,劉堯猛.基于改進交叉驗證算法的支持向量機多類識別[J].天津科技大學學報,2007,22(2):58-61. [18]YangMeng,ZhangLei,ShiuSCK,etal.GaborfeaturebasedrobustrepresentationandclassificationforfacerecognitionwithGaborocclusiondictionary[J].PatternRecognition,2013,46(7):1865-1878. IntrusionDetectionAlgorithmBasedonCompressedSensingandLeastSquareSupportVectorMachine CHENTian-yu,WUFan,MAShi-jie,LILei (NanjingUniversityofPostsandTelecommunications,Nanjing210023,China) Duetoalargeamountofrawdata,andhighdimensionandredundancyinintrusiondetection,resultingintheproblemoflowrecognition,longoperationandbadperformancefortraditionalintrusiondetectionalgorithminthefaceofmassivedatadetection,amethodofcombiningcompressedsensingandleastsquaresupportvectormachinetoapplytointrusiondetectionsystemisputforward.Innovationasfollows:Introducingcompressivesamplingtoextractthefeaturefromtheoriginaldata,thehighdimensionaldataistransformedintoalowoneonthepremiseofretainingthemainfeaturefororiginaldata;Usingleastsquaresupportvectormachinetodirectlytrainandclassifydataintheobservationdomain,andthekernelfunctionisconstructedbythecombinationofkernelfunction.Simulationshowthatusingcompressedsensingtoextractthefeaturecansignificantlyreservetheoriginalfeature.Moreover,leastsquaresupportvectormachinecanacceleratethespeedofclassifyingwithoutlosingaccuracy.Thismethodcangreatlyreducethetrainingtime,andeffectivelyimprovetheaccuracyofdetection. compressedsensing;leastsquaremethod;supportvectormachine;intrusiondetection 2015-04-21 2015-07-23 時間:2016-05-05 國家自然科學基金資助項目(61070234,61071167,61373137);國家大學生創新創業訓練計劃項目(201410293021Z) 陳天宇(1994-),男,研究方向為機器學習;李 雷,教授,博士生導師,研究方向為核方法、機器學習、模糊數理論和智能控制等。 http://www.cnki.net/kcms/detail/61.1450.TP.20160505.0814.024.html TP A 1673-629X(2016)05-0099-05 10.3969/j.issn.1673-629X.2016.05.021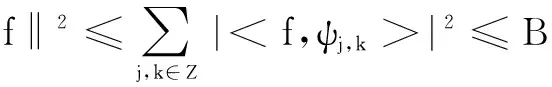



4 仿真實驗






5 結束語

