基于優化UIO的風軸速度傳感器故障檢測*
文 | 李東亮,文傳博
基于優化UIO的風軸速度傳感器故障檢測*
文 | 李東亮,文傳博
隨著風電機組裝機容量的增大,以及越來越多海上風電機組的安裝,對其故障的快速檢測和隔離提出了新要求。在大多數工業制造的機組中,只用相當簡單的方法檢測和隔離故障。
風電機組是將風能轉化成電能的裝置。在風力的作用下,驅動機組葉片和與之相連的風軸旋轉,再通過齒輪箱將旋轉速度提升,來促使發電機發電。在風速低于額定風速時,調節發電機轉子轉速,實現發電機的轉速控制,盡可能最大捕獲風能;而當風速高于額定風速時,變槳距控制能隨風速大小進行自動調節,因而能吸收盡可能多地風能并轉化為電能,實現功率的平穩輸出。速度傳感器作為整個控制系統的重要元件,在測量風軸轉速、發電機轉速方面發揮著重大作用,因此針對其進行故障診斷尤為重要。
針對風電機組傳動系統傳感器故障診斷和隔離,已有較多研究。其中大多通過Kalman算法和設計未知輸入觀測器,來診斷風軸轉速傳感器、發電機轉速傳感器和轉換器扭矩傳感器故障,但針對傳感器故障類型描述不夠具體。
本文也運用了未知輸入觀測器的方法,針對風電機組傳動系統機理模型,應用未知輸入觀測器,并通過卡爾曼濾波算法設計反饋矩陣,結合了未知輸入觀測器與Kalman濾波算法的各自優點,重構解耦了干擾,并達到了降噪的效果,采用極大似然比的方法設定閾值,從而有效地檢測出風電機組風軸轉速傳感器故障。
風電機組傳動系統模型
風電機組基準模型如圖1所示,傳動系統作為機組的重要部分,在轉速增速、制動和傳遞扭矩方面發揮著無可替代的作用。風力帶動風電機組的葉片轉動產生的機械能,通過傳動系統傳遞給發電機部分,以驅動發電機工作,從而實現能量從葉片傳遞至發電機部分。
圖1中,vw為實際風速,vw,m為實際風速的測量值,βm為實際槳距角測量值,βr為槳距角參考值,ωg為發電機實際轉速,ωg,m為發電機轉速測量值,ωr為實際風軸轉速,ωr,m為風軸轉速測量值,Pr為發電機功率參考值,τr為實際空氣動力學扭矩,τg為實際轉換器部分扭矩,τg,r為轉換器部分扭矩參考值。
根據傳動系統的動態過程,通過如下微分方程可以表示出來:
其中,θΔ表示傳動系統扭矩角,Jr和Jg分別表示低速軸轉動慣性和高速軸的轉動慣性,Kdt表示抗扭勁度,Bdt表示扭轉阻尼系數,Ng表示傳動比,ηdt表示傳動系統的效率。將上述式子寫成狀態空間方程的形式為:
由于葉片的扭矩與實際的風速有關,而風速是實變的,不可能精確地測量,因此,在此狀態下把這種測量誤差看作是未知干擾,那么傳動系統的狀態方程可寫為:
未知輸入觀測器的優化設計
通過重構并解耦干擾可得未知輸入觀測器方程為:
其中,F,G,L和H是解耦未知輸入、優化觀測器所設計的矩陣,并滿足以下方程:
通過上述觀測器的設計過程可以看出,在不考慮噪聲影響的情況下,系統干擾項可以通過干擾重構過程得到補償,達到干擾解耦的效果,但在實際系統中,噪聲往往與干擾并存,為了降低噪聲的影響,采用卡爾曼濾波算法進行反饋矩陣 的設計。
根據上述觀測器方程(1),系統殘差信號可表示為:
所以系統殘差信號可表示為:
殘差信號的協方差可表示為 :
為了方便計算,令A1=A-HCA=TA,則 殘差信號的協方差的更新過程可表示為:
其中,由于R和CP(k)CT都為正定矩陣,故存在矩陣V使得VVT=CP(k)CT+R,并令D=A1P(k)CT(HT)-1,則:
式中,當LV-d=0時,殘差信號協方差矩陣最小,可以得到:
此時,殘差信號的協方差最小為:
根據式(4)和式(5)即可計算反饋矩陣L。再結合公式(2)可構造出優化后未知輸入觀測器,進一步計算得到狀態估計值),可以計算出殘差信號的幅值。理論上,在無故障時,應該近似為零,而當出現故障時,將會偏離零值。
故障閾值的設計
實際情況下,殘差由于受系統建模精度的影響,無故障情況下難于嚴格為零,因此為了準確有效地檢測出故障信息,采用閾值門限的方法進行故障的檢測,即當殘差信號大于閾值時則系統出現故障報警。考慮到系統本身的噪聲帶來的隨機性,采用極大似然比來對殘差信號進行評估,廣義似然比的檢驗統計量定義為:
誤報率Pf是指在系統沒有發生故障時,檢測系統卻判定系統有故障發生的概率,閾值Jth的設定根據實際系統要求的誤報率滿足下式關系:
式中Pf的選擇需要權衡低誤報率和高檢測率,在選定誤報率Pf后,通過查找χ2分布表就可以確定閾值Jth,殘差信號的閾值評價邏輯為:
仿真分析
針對常見風電機組風軸轉速傳感器加性和乘性故障,在系統仿真中使用表1所示的故障信號。
在系統無故障時,對比分析了普通未知輸入觀測器與本文優化的未知輸入觀測器,如圖2所示,從仿真圖可以看出,所設計的普通未知輸入觀測器得到的殘差信號在零值附近波動較大,因此在系統無故障發生時,容易產生誤報警,而通過Kalman濾波算法設計的優化未知輸入觀測器增強了系統的魯棒性,達到了抑制噪聲的效果,故其所得殘差信號波動較小,相對普通的未知輸入觀測器更能有效地進行故障檢測。
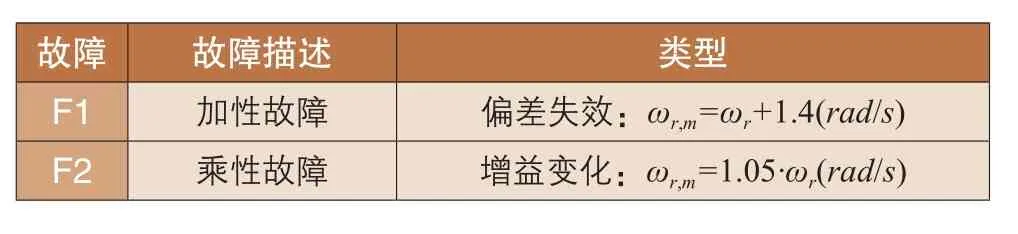
表1 仿真故障信號
通過采用最大似然比對殘差信號進行評估,選定誤報率Pf=0.0005,根據χ2分布表得到閾值Jth=11.047,對表1所示傳感器故障進行評估的仿真圖如圖3所示。
當系統在t=40s發生加性故障F1時,其仿真圖如圖3所示。從圖中可以看出,在t=40s,系統產生故障信號,仿真出的殘差信號明顯比設定的閾值要大,即系統可以準確地檢測出故障。
當系統t=40s發生乘性故障F2時,其仿真圖如圖4所示。在出現故障信號時,殘差信號會產生很大的變化,其值明顯大于所設定的閾值,表明乘性故障F2相對于加性故障更容易檢測。
所以采用這種未知輸入觀測器結合卡爾曼濾波算法的方法可以較好地達到故障檢測的效果。
結論
本文將卡爾曼濾波算法引入未知輸入觀測器進行反饋矩陣的設計,使殘差信號更好地抑制噪聲的影響,同時達到解耦干擾的效果。通過對風軸轉速傳感器加性和乘性故障進行仿真,證明所設計的觀測器能夠有效地檢測出風電機組常見轉速傳感器的故障。
(作者單位:上海電機學院電氣學院)
國家自然科學基金(61374136,61473159);上海人才發展資金(201511)。

