隨機步長無向環網通信延遲的研究
方木云,王 俊,王 超
(安徽工業大學 計算機科學與技術學院,安徽 馬鞍山 243032)
隨機步長無向環網通信延遲的研究
方木云,王 俊,王 超
(安徽工業大學 計算機科學與技術學院,安徽 馬鞍山 243032)
高性能計算機(HPC)系統期望盡可能低的通信延遲和建造成本。傳統固定步長拓撲已經無法降低通信延遲和建造成本,如固定步長環網無法突破Wong和Coppersmith給出的下界;高節點度拓撲能進一步降低延遲,但增加的交換機和物理鏈路提高了建造和運營成本。針對這兩個缺點,采用隨機步長構造方法來生成一種新型的無向環網,避免高節點度的同時,將減少節點間步長的長度從而降低通信延遲作為目標。通過仿真實驗分別對無向環網隨機步長的直徑、平均距離和固定步長的直徑下界、平均距離下界進行比較。結果表明:在一定節點度范圍內,隨機步長無向環網得到的值小于傳統固定步長環網得到的值。因此,隨機步長拓撲可成為下一代高性能計算機潛在的拓撲結構。
無向環網;固定步長;隨機步長;通信延遲
1 概 述
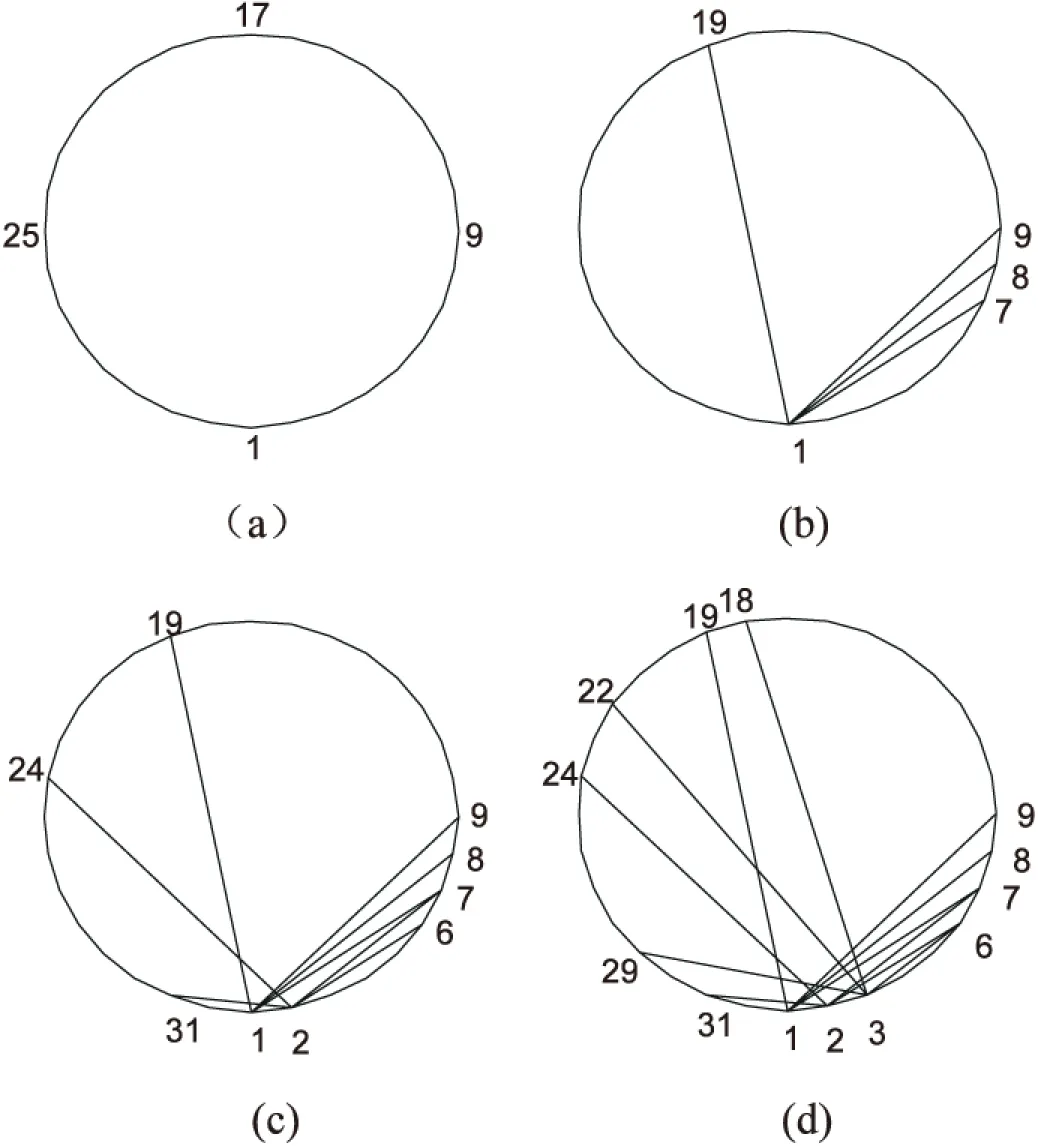
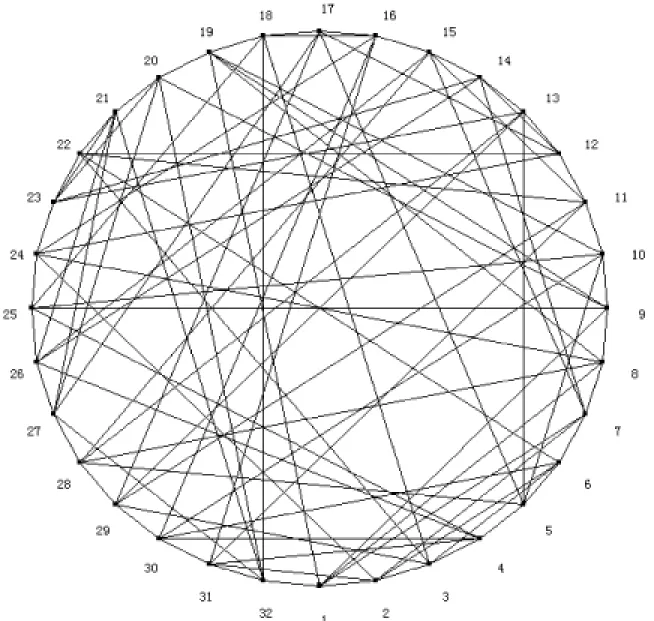
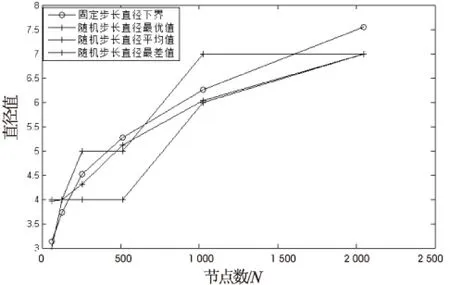
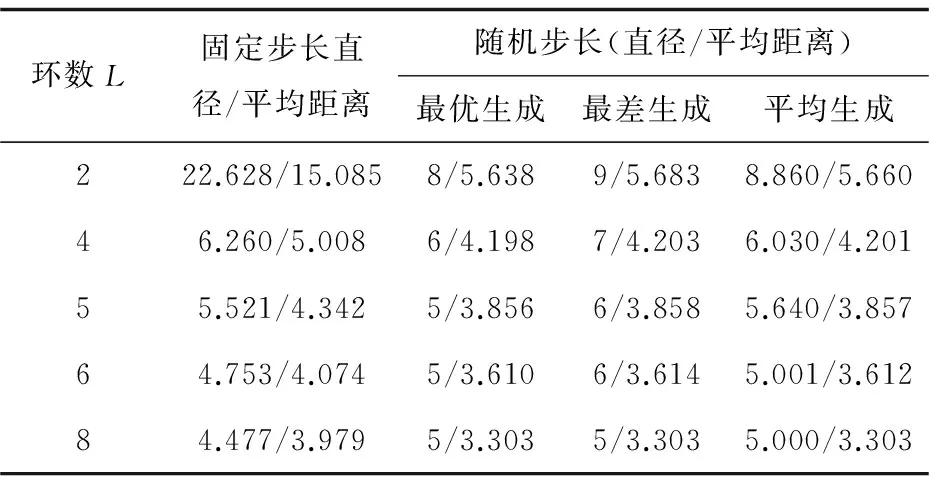
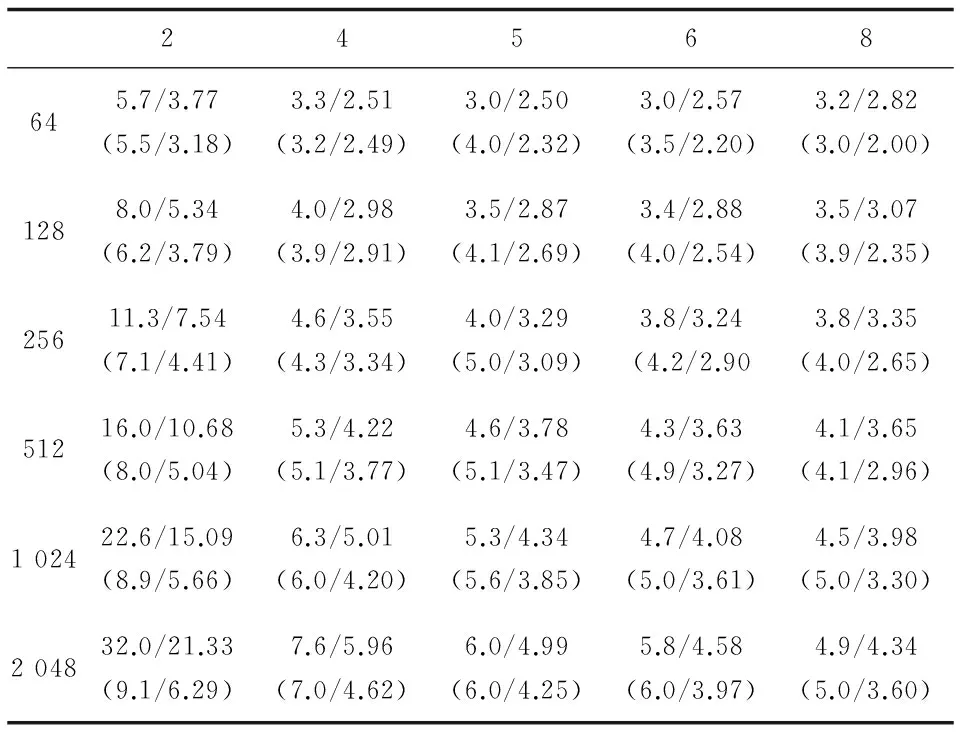
目前,高性能計算機技術已成為世界各國競相爭奪的戰略制高點,是衡量一個國家綜合國力的重要標志,以服務國家經濟建設和改善民生為最高目的,并廣泛應用于國家經濟和人民生活相關領域[1]。無向多環網絡即m(m≥2)環網絡是計算機互連網絡或通訊系統的一類重要拓撲結構,廣泛用于計算機局域網和各種并行處理結構[2-4],其圖論模型是指這樣一個無向圖G(N;±r,±m,±s),節點記為0,1,…,N-1,每個節點i向相鄰節點發出6條有向邊:i→i+r(modN)、i→i+m(modN)、i→i+s(modN)、i→i+N-r(modN)、i→i+N-m(modN)和i→i+N-s(modN),分別記為[+r]邊、[+m]邊、[+s]邊、[-r]邊、[-m]邊和[-s]邊,其中S為自然數,1≤r 2012年,日本國立情報學研究所MichihiroKoibuchi等提出在環網中采取隨機連線的方式來構造環網,在同節點數和網絡環數(即節點度)的情況下,發現網絡的通信延遲比一種用在on-chip系統上的固定步長環網的通信延遲可下降300倍,同時發現同網絡環數同節點數的隨機步長環網與現在高性能計算機(HPC)中采用的傳統環網(TORUS)等拓撲結構相比,其直徑和平均距離小、擴展性和容錯性好[9-10]。 文獻[11-12]分別指出了度量環網優越性的兩個重要參數:直徑、平均距離。直徑和平均距離越小,無向環網的節點步長長度越小,則環網中通信延遲越小。但根據MichihiroKoibuchi等的研究,仍存在不完善的地方[13-14]: (1)在同節點數和網絡環數的情況下,沒有選擇直徑和平均距離達到Wong和Coppersmith給出的下界的緊優網絡[15]來與隨機步長網絡進行對比。選作對比的非隨機步長(non-randomshortcut)網絡是固定步長環網中的最差情況之一,以此網絡與隨機步長網絡進行對比,導致隨機步長大幅降低通信延遲的這一結論可信度不高。 (2)沒有分析隨機步長構造無向m環網的直徑、平均距離分布特性。因為隨機步長的直徑是變化的,所以固定步長也是隨機步長的一個樣本,MichihiroKoibuchi等并沒有具體對比兩者在直徑和平均距離上的聯系與差異,以及沒有給出在構造無向m環網中隨機步長優于固定步長直徑和平均距離的分布特性。 (3)在同環數的情況下,隨著網絡節點數的增多,即網絡規模不斷增大,隨機步長網絡通信延遲優于固定步長網絡。對該結論沒有給出分析研究。 MichihiroKoibuchi等的工作是針對任意度的環網,為了做好橫向對比,文中針對同節點數情況下,節點度為4/6/7/8/10(即環數為2/4/5/6/8)的無向環網絡,同網絡環數情況下,不同節點數的無向環網網絡,以及將網絡環數和節點數兩者變化相結合的無向環網絡,重點分析這三個問題。 隨機步長無向環網是在傳統固定步長無向環網的基礎上構造的,在傳統固定步長環網生成時,將固定步長改為隨機步長,同時改變網絡環數。因此需依次遍歷網絡中各個節點。以節點數N=32和環數L=4為例,隨機步長無向四環網絡的生成如下: 步驟1:生成一個節點數為32的環網,如圖1(a)所示。 步驟3:逆時針依次遍歷剩下的節點,若當前節點i的度數為ik,則當前節點i可發出的隨機邊數ik'=6-ik,在節點度小于6且與i節點不相連的節點集合Gi中,若Gi的元素個數小于ik',則說明圖G中已不存在足夠的可選節點供節點i連接,返回步驟1,重新生成環網。 步驟4:重復執行步驟3,直到所有節點滿足條件。節點2的生成如圖1(c)所示,節點3的生成如圖1(d)所示。 圖1 節點1、2、3生成示意圖 由上述步驟可知,此次隨機步長無向四環網絡生成后的拓撲結構如圖2所示。 圖2 隨機步長無向四環網絡拓撲結構 3.1 隨機步長無向環網的生成算法 Step1:構建一個N*N的鄰接矩陣A[N-1,N-1],矩陣內的每個元素賦初值0;構建一個長度為N的隊列C[N-1],隊列中每個元素賦初值0,并建立一個空鏈表L,同時令網絡的環數為H,這里H≥2。 Step2:r從0到N-1循環:置A[r,(r+N-1)%N]=1和A[r,(r+N+1)%N]=1。 Step3:s從0到N-1循環(對每個s,k從s+1到N-1循環): (1)記T=C[k],若T=0,則節點r上不需要再加入隨機邊,開始下一次r循環。 (2)清空L,若A[r,k]≠1并且C[k] (3)記L中元素的個數為LLength,若LLength (4)若T=1,則在L中隨機選擇節點d1,置A[r,d1]=A[d1,r]=1,C[r]=2,C[d1]=C[d1]+1。 (5)若T=2,則在L中隨機選擇兩個互不相同節點d1,d2,置A[r,d1]=A[d1,r]=A[r,d2]=A[d2,r]=1,C[r]=2,C[d1]=C[d1]+1,C[d2]=C[d2]+1。 (7)若T=H,則在L中隨機選擇H個不相同節點d1,d2,…,dH,置A[r,d1]=A[d1,r]=A[r,d2] =A[d2,r]=A[r,d3]=A[d3,r]=…=A[r,dH]=A[dH,r]=1,C[r]=2,C[d1]=C[d1]+1,C[d2]=C[d2]+1,C[d3]=C[d3]+1,…,C[dH]=C[dH]+1。 3.2 隨機步長無向環網的直徑和平均距離求解算法 Step1:對隨機步長無向環網G=(V,E)的鄰接矩陣A進行如下變換: 其中,A是具有如下性質的N階方陣: Step2:r從0到N-1循環:對每個i,j從0到N-1循環,對每個j,k從0到N-1循環,若D[j,i]+D[i,k] 黃岡市貧困地區26家農村基層醫療衛生機構基本藥物使用情況調查 ……………………………………… 王文杰等(2):156 Step3:對Step2中得到的距離矩陣D,求出直徑[12,16]: Dia=Max(D[i,j]),0≤i,j≤N Step4:對Step2中得到的距離矩陣D,求平均距離[12]: 由文獻[12]可知傳統固定步長環網的直徑下界為: 其平均距離下界為: 文中選擇與傳統固定非單位步長無向環網的下界作對比實驗。選用VisioStudio2013中C#語言編制程序進行仿真,計算直徑和平均距離,同時將網絡拓撲結構和得到的結果數據輸入到Matlab中進行分析。 下面給出仿真實例: (1)當環數L=4不變,改變節點數時,進行100次對隨機步長無向環網的仿真實驗,對其產生的直徑的平均值和平均距離的平均值與固定步長環網的直徑下界和平均距離下界進行對比并做出相應的分析,如圖3和圖4所示,其數據對比如表1所示。 圖3 L=4時直徑對比圖 圖4 L=4時平均距離對比圖 節點數N固定步長直徑/平均距離隨機步長(直徑/平均距離)最優生成最差生成平均生成643.130/2.5043/2.4864/2.5333.970/2.4881283.723/2.9794/2.9154/2.9154.000/2.9152564.527/3.5424/3.3345/3.3564.315/3.3415125.264/4.2125/3.7656/3.7715.120/3.76810246.260/5.0086/4.1987/4.2036.030/4.20120487.545/5.9567/4.6257/4.6257.000/4.625 由圖3、4,表1得出如下結論(固定步長無向環網簡稱固定步長,隨機步長無向環網簡稱隨機步長): ①隨機步長的平均生成直徑和平均生成的平均距離均小于固定步長的直徑下界和平均距離下界。 ②隨著節點數N不斷增大,固定步長直徑下界與平均距離下界的值增加速度明顯快于隨機步長平均生成直徑和平均生成的平均距離的值增加速度。 由上述結論可知,在保持無向環網中其他因素相同時,當環數為定值,隨機步長的通信延遲優于傳統固定步長。 (2)當節點數N=1 024不變,改變網絡環數時,同樣進行相應的仿真實驗,并對其結果做出分析,如圖5和圖6所示,其數據如表2所示。 圖5 N=1 024時直徑對比圖 圖6 N=1 024時平均距離對比圖 由圖5、6和表2表明: ①隨機步長平均生成的平均距離均小于固定步長平均距離的下界。 表2 N=1 024時隨機步長與固定步長的直徑、平均距離數據對比表 ②隨著網絡環數L不斷增大,隨機步長的直徑和平均距離均小于固定步長直徑下界和平均距離下界的趨勢越來越不明顯。 由上述兩點,在保持無向環網中其他因素相同時,當網絡環數(即節點度)在一定范圍內,隨機步長的通信延遲優于傳統固定步長,這一點也避免了高節點度拓撲所帶來的建造和運營成本的問題。 (3)結合實驗(1)、(2),同時改變節點數N和網絡環數L,進行100次直徑和平均距離對比實驗,并對結果做出分析。實驗結果如表3所示。 表3 固定步長直徑/平均距離(隨機步長直徑/平均距離) 分析其總體趨勢如下: ①當L≤4(即節點度≤6)不同節點數時,隨機步長直徑、平均距離均小于固定步長直徑下界和平均距離下界;當L≥5時,隨機步長直徑≥固定步長直徑下界,但隨機步長平均距離≤固定步長平均距離下界。 ②當L一定節點數不斷增加時,隨機步長直徑和平均距離的值增加速度明顯小于固定步長直徑下界和平均距離下界的值增加速度;當N一定環數不斷增加時,雖然隨機步長直徑≥固定步長,但隨機步長直徑的值增加速度相比固定步長直徑下界的值增加速度較慢,且隨機步長平均距離均小于固定步長平均距離下界。 綜上,在保持無向環網中其他因素相同時,當網絡環數(即節點度)在一定范圍內,隨機步長得到的直徑、平均距離均小于傳統固定步長直徑下界、平均距離下界,則隨機步長網絡節點步長長度較小,從而得出結論:在無向環網中,隨機步長較傳統固定步長通信延遲占有優勢。 文中采用隨機步長來構造無向環網,分別對隨機步長無向環網直徑、平均距離和固定步長無向環網直徑下界、平均距離下界進行仿真實驗對比。結果表明,在保持無向環網中其他因素相同時,當節點度在一定范圍內,隨機步長無向環網的網絡通信延遲和網絡性能均優于固定步長無向環網,同時隨著網絡節點數不斷增加,即網絡規模的不斷增大,隨機步長降低通信延遲的優勢更加明顯。因此,與當前主流的HPC采用的高節點度和固定步長拓撲結構相比,隨機步長拓撲可成為下一代高性能計算機的潛在拓撲結構。 [1] 周興銘.高性能計算技術發展[J].自然雜志,2011,33(5):249-254. [2]ChenCY,HwangFK.EquivalentL-shapesofdouble-loopnetworksforthedegeneratecase[J].JournalofInterconnectionNetworks,2000,1(1):47-60. [3] 陳協彬.步長有限制的雙環網絡的最優路由算法[J].計算機學報,2004,27(5):596-603. [4]HwangFK.Asurveyonmulti-loopnetworks[J].TheoreticalComputerScience,2003,299(1):107-121. [5] 方木云,屈玉貴,趙保華.雙環網絡的[+h]邊優先尋徑策略[J].計算機學報,2008,31(3):536-542. [6] 蘇小虎,方木云,邰偉鵬,等.雙環網絡G(N;1,s)的L形瓦仿真算法改進[J].小型微型計算機系統,2012,33(9):2053-2055. [7] 方木云,趙保華,屈玉貴.非單位步長雙環網絡G(N;r,s)的L形瓦仿真算法[J].系統仿真學報,2006,18(10):2963-2965. [8]WongCK,CoppersmithD.Acombinatorialproblemrelatedtomulti-modulememoryorganizations[J].JournalofACM,1974,21(3):392-402. [9]KoibuchM,MatsutaniH,AmanoH,etal.AcaseforrandomshortcuttopologiesforHPCinterconnects[C]//Procof39thannualinternationalsymposiumoncomputerarchitecture.[s.l.]:IEEE,2012:177-188. [10]KimJ,BalfourJ,DallyW.Flattenedbutterflytopologyforon-chipnetworks[C]//Proceedingsofthe40thannualIEEE/ACMinternationalsymposiumonmicro-architecture.[s.l.]:IEEEComputerSociety,2007:172-182. [11] 方木云,侯海金,吳愛清,等.雙環網絡直徑點和寬直徑點的分布特性[J].小型微型計算機系統,2013,34(4):749-752. [12] 陳業斌,李 穎,鄭 嘯,等.關于有向環網平均直徑的研究[J].通信學報,2013,34(2):138-146. [13]FujiwaraI,KoibuchiM,CasanovaH.Cabinetlayoutoptimizationofsupercomputertopologiesforshortercablelength[C]//Procof13thinternationalconferenceonparallelanddistributedcomputing,applicationsandtechnologies.[s.l.]:IEEE,2012:227-232. [14]KoibuchiM,FujiwaraI,MatsutaniH,etal.Layout-consciousrandomtopologiesforHPCoff-chipintercomnects[C]//Procof19thinternationalsymposiumonhighperformancecomputerarchitecture.[s.l.]:IEEE,2013:484-495. [15] 方木云,趙保華,屈玉貴.基于圈的緊優雙環網絡G(N;1,s)求解算法[J].華中科技大學學報:自然科學版,2005,33(6):17-19. [16] 方木云,趙保華.新的無向雙環網絡G(N;±1,±s)直徑求解方法[J].通信學報,2007,28(2):124-129. Research on Communication Delay of Random-step Undirected Loop Networks FANG Mu-yun,WANG Jun,WANG Chao (School of Computer Science and Technology,Anhui University of Technology,Ma’anshan 243032,China) High-performance computer system expects the lowest possible communication delays and construction costs.Traditional fixed-step topology has been unable to reduce communication latency and construction costs.For example,fixed-step loop networks cannot break through the lower bound given by Wong and Coppersmith,and high degree of topological node can further reduce latency,but increased switch and physical links improve the construction and operating costs.In view of two shortcomings,random-step is used to construct a new type of undirected loop networks which can reduce the length of steps between nodes to reduce the communication delay as the destination,at the same time can avoid high degree of node.Respectively compares diameter and average distance of random-step undirected loop networks as well as lower diameter and average lower distance of fixed-step through simulation experiments.The results show that within a certain range of the node,the value of the random-step to the ring obtained less than the value of traditional fixed-step ring obtained.Thus,random-step topology may be the next generation of high-performance computer underlying topology. undirected loop networks;fixed-step;random-step;communication delay 2016-01-08 2016-04-13 時間:2016-09-19 國家自然科學基金資助項目(61003311);安徽省教育廳重大項目(ZD2008005-1) 方木云(1968-),男,教授,博士,研究方向為計算機網絡、網絡拓撲結構等;王 俊(1990-),男,通信作者,碩士研究生,研究方向為計算機網絡與網絡拓撲結構。 http://www.cnki.net/kcms/detail/61.1450.TP.20160919.0843.062.html TP393 A 1673-629X(2016)10-0027-05 10.3969/j.issn.1673-629X.2016.10.0062 隨機步長無向環網的生成

3 仿真算法
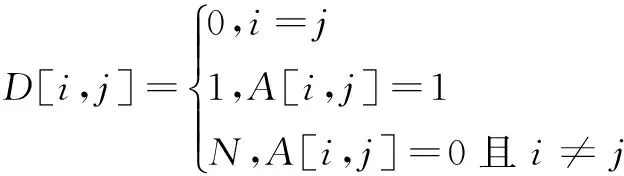
4 仿真實驗及結果分析
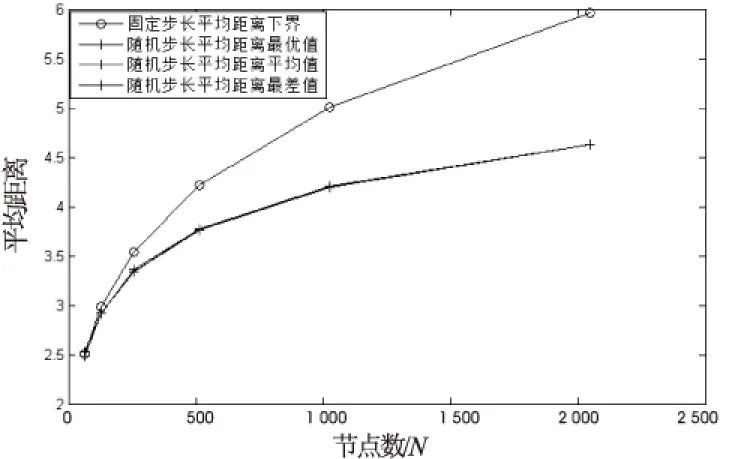
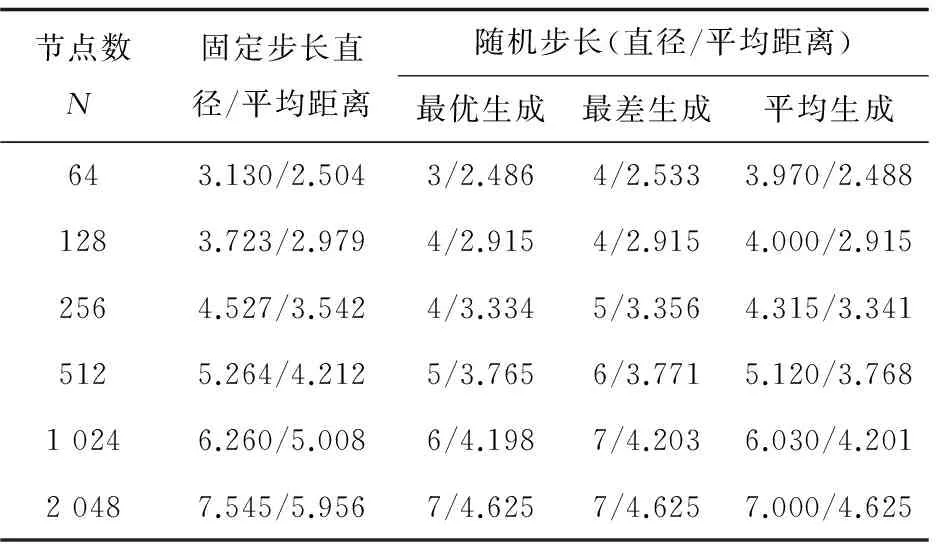
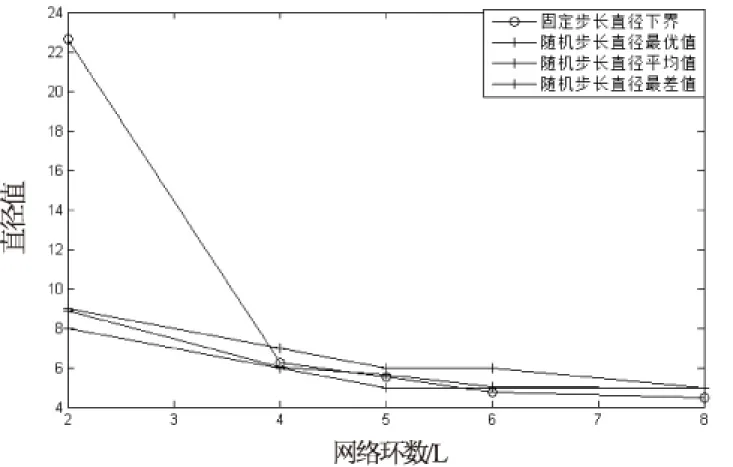
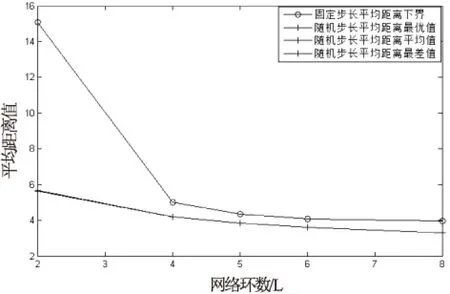
5 結束語

