一種新型的快速信號重構算法

錢 陽，宋歡歡，李 雷

(南京郵電大學 視覺認知計算與應用研究中心，江蘇 南京 210023)

一種新型的快速信號重構算法

錢 陽，宋歡歡，李 雷

(南京郵電大學 視覺認知計算與應用研究中心，江蘇 南京 210023)

信號重構是壓縮感知理論的關鍵組成部分，研究快速有效的重構算法具有現實意義。目前，迭代閾值算法中的不動點迭代(FPC)算法，在重構速度和精度方面存在很大的提升空間。為此，文中首先提出了一種快速不動點迭代(FFPC)算法。接著針對該算法，通過引入子空間優化，充分利用壓縮感知貪婪算法和凸優化算法的各自優點，提出了快速不動點_活動集(FFPC_AS)算法，進而得到更加準確的解。對于FFPC_AS算法，給出了收縮階段和子空間優化階段交替執行方案，避免了除偏(Debiasing)操作。大量仿真對比實驗表明，所提算法既能快速重構圖像信號，又可以提高準確率。

壓縮感知；快速不動點；活動子集；子空間優化；除偏

0 引 言

在信息數字化時代，壓縮感知理論(Compressed Sensing,CS)[1-2]憑借其采樣與壓縮同時進行，并能精確重構出原始信號的良好性能，吸引了數學家和計算機學家的廣泛關注[3]。該理論主要包括信號的稀疏表示、觀測矩陣的選取和信號重構這三個階段。其中最關鍵的一步是重構信號，其性能的好壞決定了重構質量的優劣與恢復時間的長短。

CS理論的目標是從較少的相對不完整的測量值b=Ax中恢復出K稀疏信號x∈Rn。目前重構算法主要集中于貪婪算法和凸優化算法。當滿足等距約束條件(RestrictedIsometryProperty,RIP)[4]時，貪婪算法效果較好。這類算法主要包括正交匹配算法(OMP)[5]、子空間追蹤(SP)[6]等。而典型的凸優化算法包括基于閾值的算法[7-8]、NESTA算法[9]、不動點連續方法(FixedPointContinuation，FPC)[10]等。

FPC算法是一種基于算子分裂和連續的，能夠解決大規模數據密集問題的方法，被廣泛應用于CS的核磁共振成像(MRI)中[11]。為了提高FPC算法的重構性能，文中通過引入軟閾值和正則化參數的雙收縮，提出了快速不動點迭代方法(FFPC)。該方法表現出更優的重構性能。然而，FFPC方法重構的信號存在一些誤差，需要采用除偏操作去除誤差較大的元素。受文獻[12]中所提基于收縮的快速稀疏重構(FPC_AS)算法的啟發，針對輸入信號絕對稀疏時，FFPC算法重構誤差較大的情況，文中通過引入子空間優化概念，建立了快速不動點-活動子集算法(FFPC_AS)。大量對比實驗驗證了所提算法無需除偏，而且具有最好的重構效果。

1 預備知識

1.1 壓縮感知理論基礎

在壓縮感知理論中，如果n維稀疏信號x∈Rn在某正交基或者緊框架Ψ(其中Ψ=(φ1,φ2,…,φn)T)上可壓縮，那么x在該基下可以線性表示為：

Θ=ΨTx

(1)

式中，Θ是x在Ψ變換域上的變換向量。

CS編碼中，通過設計一個平穩的、與Ψ不相關的測量矩陣Φ，對稀疏信號Θ進行非自適應觀測，得到觀測向量b=ΦΘ=ΦΨTx(其中A=ΦΨT稱為信息算子[13])。Candes等指出，為保證準確地從m個測量值中恢復出K個系數，A必須滿足等距性質[14]。

實際的信號測量中，隨著被測信號的不同，變換基Ψ會有相應的變化，因此希望找出可以與任意稀疏基不相關的觀測陣Φ。對于任意正交基Ψ，隨機產生一個測量矩陣Φ，若m≥CKlog(n/K)，其中C為某固定常數，則Ψ與Φ不相關的概率就很大，即A滿足RIP條件的概率很大。常用的觀測陣有高斯隨機矩陣、哈達瑪矩陣、伯努利矩陣等。

min‖x‖0subject toAx=b

(2)

然而，l0范數模型是NP難題[15]，在數值上是不可解的。因此，Candes等指出，在一定條件下，問題的解x∈Rn可以通過基追蹤問題(BP)獲得。

(3)

通過引入正則化參數μ，式(3)可以化為無約束最優化問題。

(4)

1.2 基于不動點方法的信號重構算法

2007年，Elaine T等首次提出解決l1范數問題的不動點算法(FPC)，并將其應用于CS的信號重構中。FPC主要解決式(5)所示的l1范數問題：

(5)

其不動點迭代式為：

xk+1=Sv°h(xk),ν=τ/μ

(6)

其中，Sv(·)是軟閾值收縮算子；ν是閾值。

2010年，WenZaiwen等提出了一種基于收縮的快速稀疏重構算法—FPC_AS[16]，用于求式(5)的最優解。該算法是在FPC算法的基礎上，引入子空間優化，集成了閾值迭代算法求解速度快和凸優化算法易獲得全局解的優勢，從而得到式(5)更加精確的解。盡管如此，FPC算法在重構速度和精度方面仍存在很大的提升空間。

2 快速不動點迭代算法(FFPC)

傳統FPC方法的收斂速度由ν=τ/μ和二次函數f(x)的部分Hessian矩陣HEE的譜性質決定，在特定的參數τ下，不動點方法是線性收斂的。為提高FPC算法的收斂速度和信號重構質量，引入軟閾值步長參數和正則化參數的收縮，提出了快速不動點迭代算法。

FFPC算法求解的是問題(5)中M=2的情況，其中μ是引入的正則化參數，用來平衡l1,l2范數所占的比重，利用優化算法可求得最優解x*。

(7)

(8)

使用式(8)更新x類似于使用最速下降方法，在滿足式(9)的基礎上，使用式(10)來尋找最優步長tk。

(10)

因此，更新不動點迭代式(6)為：

式中，⊙是按元素逐個作乘積的算子；ν=τ/μ為閾值，對確定不動點迭代式(11)的收斂速率起重要作用，ν值越大，收斂速率越快。因此只要使τ的值盡量大，μ的值盡量小，就能加快不動點迭代(11)的收斂速度。

利用BB(Barzilai和Borwein)步長更新參數τ。

(12)

對于參數μ，其作用是來平衡二次項f(x)和l1范數項‖x‖1的比重，通常設置δ·max(ATb)(δ是大于0的常數)作為參數μ的初始值。此外，在迭代過程中，為加快x的稀疏速度，可以對μ作適當的收縮操作，即令μ=β·μ(其中β是收縮因子，0<β<1)，并且保證μ仍然能夠平衡二次函數f(x)和l1范數‖x‖1在迭代過程中的比重。

在FFPC算法中，兩次相鄰迭代的相對誤差決定了其迭代終止條件：

這里，迭代終止條件為xtol和gtol。當滿足上述條件時，FFPC算法停止迭代。

利用FFPC算法恢復信號x，具體執行步驟如下：

Step1：令信號在小波域的稀疏表示為x0=0，設置迭代次數初始值k=1,t1=1,z1=0。

Step2：利用式(6)計算xk。

Step3：計算tk+1，根據式(9)對t進行更新，利用式(8)計算zk。

Step4：按式(13)計算函數Gk(xk,xk-1)，若滿足終止條件，則令x*=xk，否則轉Step5。

Step5：擴張參數μ=β·μ，令k=k+1，更新τ，將zk代入Step2中，重復上述過程。

迭代結束后，得到的迭代結果x*即是對原始信號的估計值。

3 快速不動點_活動子集(FFPC_AS)

盡管FFPC算法比FPC算法表現出更優的重構性能，但和FPC算法一樣，重構出的信號存在一些誤差，需要采用除偏操作去除誤差比較大的元素。針對在輸入信號絕對稀疏時，FFPC算法重構結果誤差較大的情況，受文獻[16]的啟發，文中提出了快速不動點-活動集算法(FFPC_AS)。該方法在利用FFPC重構信號后，通過提取重構結果非零項的索引，建立活動子集，并進行子空間優化操作，在確保信號重構準確度的基礎上，提高算法收斂速度。

FFPC_AS算法分為收縮階段和子空間優化階段。收縮階段利用FFPC算法逼近原始信號x，得到粗糙解xk，并且計算活動集A(xk)；當活動集A(xk)逼近于真實的活動集A(x*)時，利用二階方法求解子空間優化問題即可。不斷地重復這兩個階段，直至滿足精確解條件。

3.1 收縮階段

令dk=d(τk)(xk)為線性搜索的搜索方向，則dk可以按照下面方法進行計算。

dk(x)=xk-xk-1,k>1

(14)

其中，xk是FFPC算法第k步迭代得到的結果，令x+=xk+αkdk，則不動點迭代式為：

xk=S(x+-τg,τ/μ)，μ>0,τ>0

(15)

(16)

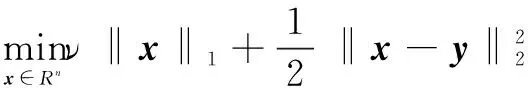
(S(x,ν)-x)T(y-S(x,ν))+ν(ξ-

‖S(x,ν)‖1)≥0

(17)

用x-τg和‖x‖1，分別替換y和ξ，并且令ν=τ/μ，則式(17)可寫為：

(S(x-τg,τ/μ)-(x-τg))T(x-S(x-τg,τ/μ))+τ/μ(‖x‖1-‖S(x-τg,τ/μ)‖1)≥0

代入式(14)、(15)得：

(18)

minμf(x)+ξs.t. (x,ξ)∈Ω

(19)

因為ξ*=‖x*‖1，故其對于不動點x*的一階最優性條件為：

μf(x*)(x-x*)+(ξ-‖x*‖1)≥0 ?(x,ξ)∈Ω

(20)

因此，用dk求解問題(5)類似于求解式(19)的梯度投影方法，當且僅當x*是式(15)的駐點時，對?x*∈Rn,0<τ<∞,有：

d(τ)=0

(21)

ψ(xk+αkdk)≤Ck+ρhσΔk

(22)

(23)

由于式(18)和l1范數的凸性，故存在(回溯)步長滿足式(22)的要求，其中Ck=Φ(xk)。該線性回溯方法是單調的，因為Φ(xk+1)<Φ(xk)。

FFPC_AS算法中使用了一種快速的非單調的線性搜索方法—FNMLS。

Ck+1=(ηQkCk+ψμ(xk+1))/Qk+1

(24)

其中，Ck是函數ψμ(xk)和Ck-1的凸組合；Qk+1=ηQk+1,Q0=1,0<η<1。

算法過程如下：

初始化：x0，設置參數0<η<1,t0=1和0<τm<τM<∞。

令C0=Φ(x0),Q0=1,k=0。

WHILE“不滿足收斂條件”DO

計算搜索方向：令τm<τk<τM，令dk=S(x+-τkgk,τk/μ)-xk-1。

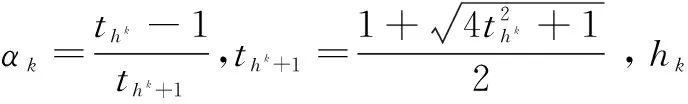
更新：令Qk+1=ηQk+1，Ck+1=(ηQkCk+

Φ(xk+1))/Qk+1，k=k+1。

ENDWHILE

在迭代過程中，Ck的值隨著迭代次數的增加而變大。

3.2 子空間優化階段

對于固定的常數δ，滿足下面任意一個條件，即可由收縮階段轉換到子空間優化階段。

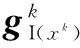
(25)

(26)

(27)

至此，子空間優化為可簡化為：

minφμ(x) s.t.x∈Ω(xk)

(29)

該子空間優化問題可以由共軛梯度方法來求解。

FFPC_AS算法：

(2)重復迭代直至收斂。

●閾值收縮階段。

令tk=1。若ψμk(xk+)>Ck+σαkΔk，那么用FNMLS算法搜索αk。更新x+=xk+αkdk，Qk+1=ηQk+1，Ck+1=(ηQkCk+Φ(xk+1))/Qk+1。

計算非活動集I(xk+1,ξk)和活動集A(xk+1,ξk)，更新閾值ξk+1=min(max(η2

若χ(xk+1,μ,ξk)≤max(ε,εxmax(‖xk+1‖,1))，則收縮階段結束。

●檢查是否需要做子空間優化。

令do_sub=0，若I(xk,ξk-1)≠I(xk+1,ξk)，則

設置do_sub=1,δ=γδ。否則若

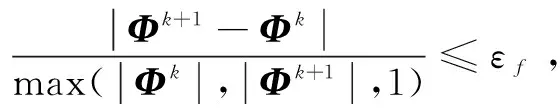
●做子空間優化。

若do_sub=1，那么

若χ(xk+1,μ,ξk)≤max(ε,εxmax(‖xk+1‖,1))，則返回結果集。

若χ(xk+1,μ,ξk)≤max(ε,εxmax(‖xk+1‖,1))或者do_sub=1，并且μk>μ，那么

計算μk+1=max(βmin(‖gA(xk+1,ξk)‖,μk),μ)。令δ=δ0,Ck+1=Φ(xk+1),Qk+1=1。

否則令μk+1=μk。

4 仿真實驗及實驗結果分析

以256*256的自然圖像Camera進行實驗仿真。實驗平臺為Windows8.1，Intel(R)Core(TM)2DuoCPU，2.53GHz，實驗設計基于Matlab7.11.0編程實現。采用DCT稀疏變換基，觀測矩陣選用高斯隨機矩陣。初始正則化參數μ=10-10。迭代過程中，設置收縮因子β=0.1，非線性搜索參數γ=0.85，σ=0.5，δ=10-6，執行子空間優化條件參數εf=10-20。

圖1 算法性能隨采樣率變化圖

圖1記錄了隨著采樣率變化不同算法對Camera圖像重構性能的變化曲線。

實驗中，由于FPC_AS、FFPC_AS算法均采用一階收縮方法和二階共軛梯度(CG)方法交替求解的方式來逼近最優解，而其他算法則是一階算法，故FPC_AS與FFPC_AS算法的收斂速度要快些。圖(a)形象地展現了FPC_AS和FFPC_AS的重構速度。當采樣率超過0.6時，二階子空間優化次數較多，算法收斂至精確解的速度更快。圖(b)展示了在不同采樣率下，FFPC_AS算法重構出的圖像的峰值信噪比都是最高的。

表1給出了不同采樣率下對FPC和FFPC算法所得結果進行除偏操作的重構情況。

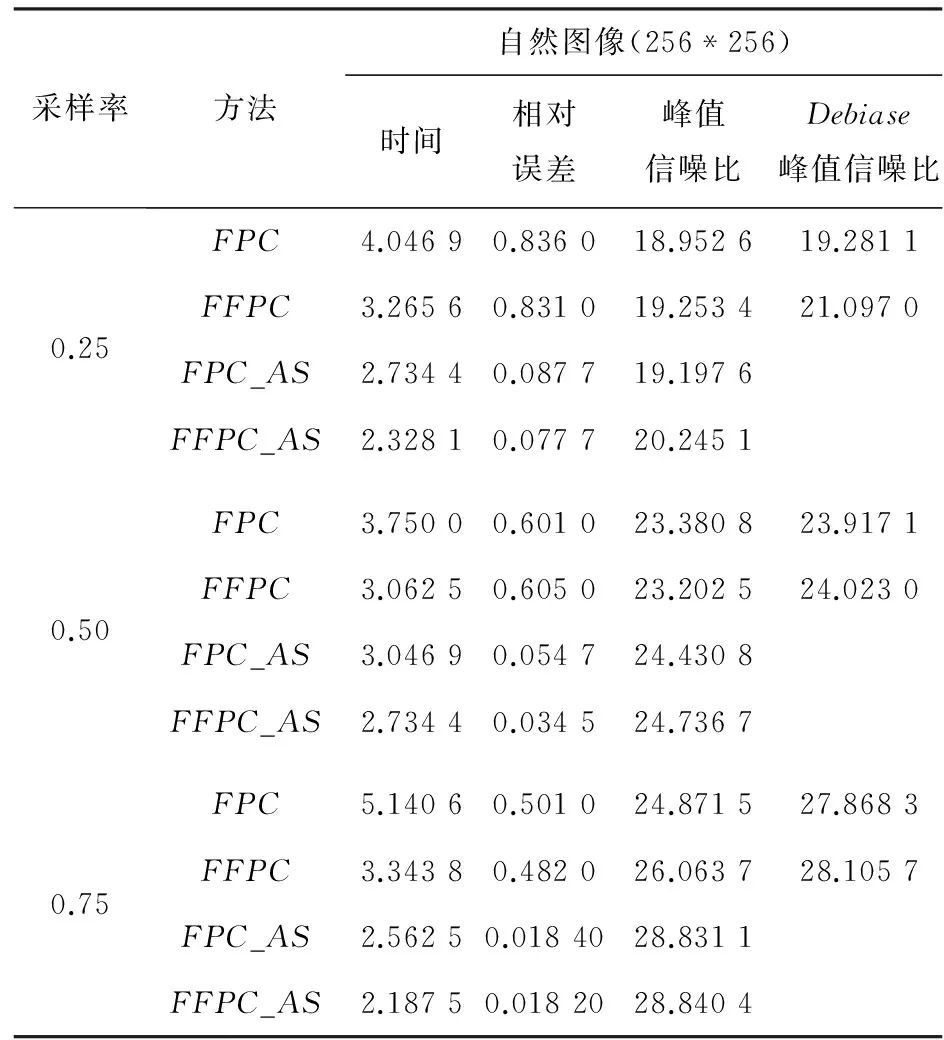
表1 Camera圖像處理結果

由表1可見，FFPC_AS算法重構速度最快，在采樣率為0.5和0.75時，FFPC_AS的峰值信噪比要比FFPC經過除偏(Debiase)的值要高出0.713 7dB和0.734 7dB。

為驗證文中算法重構性能最優，分別采用FPC_AS和FFPC_AS算法對Camera圖像進行重構。圖2和圖3分別給出了不同采樣率下兩種算法的重構效果直觀圖。

圖2 自然圖像Camera的FPC_AS處理結果

圖3 自然圖像Camera的FFPC_AS處理結果

從圖中不難發現，FFPC_AS的重構效果更好些。在采樣率為0.25和0.5時，結果圖中均存在些噪點，FFPC_AS的重構圖細節更加明顯。而當采樣率達到0.75時，兩種方法的重構圖像細節突出，對比度很高。

5 結束語

文中首先對傳統的不動點迭代方法(FPC)進行改進，通過引入軟閾值步長參數和正則化參數的收縮，形成快速不動點迭代(FFPC)算法；接著針對FFPC算法需要進行除偏操作的缺陷，提出了快速不動點-活動子集(FFPC_AS)方法。該算法結合了一階FFPC方法和二階共軛梯度方法的優勢，在FFPC算法求得結果的活動子集逼近精確解的活動子集時，利用二階共軛梯度方法再來逼近精確解，不僅能使FFPC_AS算法更快速地收斂至最優解，而且大大提高了解的準確度。仿真實驗結果表明，文中所提算法在圖像重構的質量和速度方面有明顯優勢。

[1]CandesE,RombergJ.Quantitativerobustuncertaintyprinciplesandoptimallysparsedecompositions[J].FoundationsofComputationalMathematics,2006,6(2):227-254.

[2]DonohoDL,TsaigY.Extensionsofcompressedsensing[J].SignalProcessing,2006,86(3):533-548.

[3]KashinBS,TemlyakovVN.Aremarkoncompressedsensing[J].MatematicheskieZametki,2007,82(6):829-837.

[4]CandesE,TaoT.Nearoptimalsignalrecoveryfromrandomprojections:universalencodingstrategies[J].IEEETransactionsonInformationTheory,2004,52(12):5406-5425.

[5]MallatS,ZhangZ.Matchingpursuitswithtime-frequencydictionaries[J].IEEETransactionsonSignalProcessing,1993,41(12):3397-3415.

[6]DaiW,OlgicaM.Subspacepursuitforcompressivesensing:closingthegapbetweenperformanceandcomplexity[R].Urbana,IL:UniversityofIllinoisatUrbana-Champaign,2008.

[7]CombettesPL,PesquetJC.Proximalthresholdingalgorithmforminimizationoverorthonormalbases[J].SIAMJournalonOptimzation,2007,18(4):1351-1376.

[8]BeckA,TeboulleM.Afastiterativeshrinkage-thresholdingalgorithmforlinearinverseproblems[J].SIAMJournalonImagingScience,2009,2(1):183-202.

[9]BeckerS,BobinJ,CandesE.NESTA:afastandaccuratefirst-ordermethodforsparserecovery[R].Pasadena:CaliforniaInstituteofTechnology,2009.

[10]HaleET,YinW,ZhangY.Fixed-pointcontinuationforl1-minimization:methodologyandconvergence[J].SIAMJ.Optim.,2008,19(3):1107-1130.

[11] 劉曉曼，叢 佳，朱永貴.不動點方法及其在壓縮感知核磁共振成像中的應用[J].中國傳媒大學學報:自然科學版，2014,21(1):28-34.

[12]HaleET,YinWotao,ZhangYin.Afastalgorithmforsparsereconstructionbasedonshrinkage[J].SIAMJournalonScientificComputing,2010,32(4):1832-1857.

[13]BaraniukR.Alectureoncompressivesensing[J].IEEESignalProcessingMagazine,2007,24(4):118-121.

[14]CandesE,RombergJ,TaoTerence.Robustuncertaintyprinciples:exactsignalreconstructionfromhighlyincompletefrequencyinformation[J].IEEETransactionsonInformationTheory,2006,52(2):489-509.

[15] 焦李成，公茂果，王 爽，等.自然計算、機器學習與圖像理解前沿[M].西安:西安電子科技大學出版社,2008.

[16]WenZ,YinW,GoldfarbD,etal.Ontheconvergenceofanactivesetmethodforl1minimization[R].NewYork:ColumbiaUniversity,2008.

A Novel Fast Signal Reconstruction Algorithm

QIAN Yang,SONG Huan-huan,LI Lei

(Center for Visual Cognitive Computation and Its Application,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)

Signal recovery is the key component of compressed sensing theory,which has practical significance to research the fast effective reconstruction algorithms.At present,the convergence rate and accuracy of Fixed Point Continuation (FPC) algorithm still can be improved.So,a Fast Fixed-Point Continuation (FFPC) algorithm is put forward firstly,and then it makes full use of the respective advantages of greedy algorithm and convex optimization by introducing subspace optimization to come up with the fast Fixed-Point Continuation_Active Set (FFPC_AS) algorithm,which can improve the accuracy and the convergence rate of FFPC algorithm.For the FFPC_AS algorithm,the shrinkage phase and subspace optimization phase are performed repeatedly which can avoid the debiasing operation,and the embodiment of the two stages is given in this paper.A large number of comparative simulation results show that the proposed algorithm exhibits state-of-the-art performance in terms of both its speed and its ability to recover sparse signal.

compressed sensing;fast fixed-point continuation;active set;subspace optimization;debiasing

2015-09-21

2015-12-23

時間：2016-05-25

國家自然科學基金資助項目(61070234，61071167，61373137，61501251)；南京郵電大學引進人才科研啟動基金資助項目(NY214191)；江蘇省2015年度普通高校研究生科研創新計劃項目(KYZZ15_0235)

錢 陽(1991-)，女，碩士生，研究方向為非線性分析及應用；李 雷，博士，教授，研究方向為智能信號處理和非線性科學及其在通信中的應用研究。

http://www.cnki.net/kcms/detail/61.1450.TP.20160525.1709.058.html

TP301.6

A

1673-629X(2016)06-0056-06

10.3969/j.issn.1673-629X.2016.06.012