基于優化組合核極限學習機的網絡流量預測

劉 悅，王 芳

(開封大學 信息工程學院，河南 開封 475004)

基于優化組合核極限學習機的網絡流量預測

劉 悅，王 芳

(開封大學 信息工程學院，河南 開封 475004)

為了提高網絡流量預測的精度，針對網絡流量數據具有非線性、非平穩的特點，提出一種基于經驗模態分解(EMD)和混沌粒子群算法優化組合核極限學習機的網絡流量預測模型。首先將網絡流量時間序列進行EMD分解，提取網絡流量數據的各個分量，然后分別對各個分量采用核極限學習機進行預測，最后重構出預測結果。針對傳統核極限學習機擬合能力的不足，提出一種基于高斯核和多項式核組合的組合核極限學習機，并且采用改進的混沌粒子群算法優化組合核的核參數組合權值以及懲罰因子，并將其應用到網絡流量預測中。實驗結果表明，該方法可以有效提高網絡流量預測的精度，有助于指導網絡資源的合理分配和規劃。

網絡流量預測；核極限學習機；組合核函數；混沌粒子群；經驗模態分解

0 引 言

隨著互聯網技術的飛速發展，流量和帶寬不斷增加，網絡規模和網絡的復雜程度日益增大，導致網絡管理工作的繁重程度急劇上升，網絡故障頻現。為了保證互聯網數據的可靠傳輸和資源的合理分配，高質量的網絡流量預測對網絡的規劃、管理和設計具有重要的理論意義和實際價值[1-2]。

核極限學習機算法是新加坡學者黃廣斌提出的一種新的前饋神經網絡學習算法[3]。它計算速度快，泛化性好，得到了廣泛應用[4-6]。文中針對網絡流量數據的非平穩和非線性的特點，提出了結合經驗模態分解(EMD)和核極限學習機的網絡流量預測算法。首先采用EMD對原始時間序列進行分解，然后將分解出來的各個分量分別采用核極限學習機進行預測，最后重構出預測結果。針對核極限學習機逼近能力的不足，提出一種基于徑向基核函數和多項式核函數組合的多核極限學習機方法，并且采用改進的混沌粒子群算法去優化多核極限學習機的參數。該方法為網絡資源的合理配置和可靠傳輸提供決策的依據。

1 經驗模態分解

EMD是一種自適應信號分解法，其吸取小波變換多分辨的優點的同時，克服了小波基選擇和分解尺度難以確定的缺點，因此非常適合非線性非平穩信號的分解[7-8]。網絡流量時間序列是一個典型的非平穩時間序列[9]，文中采用先EMD分解，再預測、重構的方法。

2 CPSO組合核極限學習機

2.1 核極限學習機

Huang等研究前饋神經網絡無需像BP那樣迭代求解，而是可以通過隨機設置前饋神經網絡的輸入權值，通過求解輸出權值的最小二乘解來完成訓練[10]。極限學習機因其極快的訓練速度和良好的泛化性，已經受到很多學者的關注。在求解極限學習機的過程中，既要考慮使訓練誤差達到最小，還要考慮到結構風險最小化。因此需要在最小化的輸出權值和最小化的誤差之間做出折中，可以構造如下的計算公式：

(1)

也可以表達如下:

(2)

根據KKT條件，可以定義Lagrange函數求解上面的問題，也就是說上面的問題可以等效為求解下面的公式：

相應的優化限制條件為：

(4)

式中，H是隱含層輸出矩陣的權值，隨機給定以后它就是一個固定的矩陣，它的數值僅僅與輸入樣本的個數和設置的隱層節點數有關。

把上述公式進行組合，可以得到：

?

(5)

其中：

(6)

于是上面公式可以合并寫成:

(7)

最終可以推導得到:

(8)

于是極限學習機的逼近函數可以寫成:

(9)

可以看出,無論是h(xi)HT還是HHT都是矩陣內積的形式，可以構造一個滿足mercer定理的核函數來代替這個內積,于是有如下公式：

(10)

于是核極限學習機的逼近函數可以寫成:

(11)

2.2 組合核極限學習機

只要滿足mercer定理的核函數都可以作為極限學習機的核函數，如高斯徑向基核函數(RBF)、多項式核函數(polynomial)等，但是往往每個核函數在不同的應用領域都各有它的優勢，而且單獨的一個核函數往往并不能達到最佳的逼近效果[10-14]，所以文中提出了一種基于組合核的極限學習機算法，可以構造權重對不同的核函數進行加權組合。

文中采用徑向基核和多項式核加權組合的方式來構造多核核函數。RBF核是一種局部核函數，多項式核是一種全局核函數，局部核函數的學習力比較強，而全局核函數泛化力強，學習能力弱，因此兩者組合能發揮出比較好的效果。

RBF核公式為：

k(x,xi)=exp(-‖x-xi‖2/a)

多項式核公式為：

k(x,xi)=(xxi+1)q

混合核函數的公式為：

k(x,xi)=p(xxi+1)q+(1-p)exp(-‖x-xi‖2/a)

(12)

文中把這種采用了多核組合的核極限學習機稱之為多核極限學習機(Multi Kernel Extreme Learning Machine，MKELM)。

2.3 混沌粒子群算法(CPSO)

針對傳統PSO算法存在早熟的問題，將混沌理論引入粒子群算法對其進行改進，其算法具體流程如下：

(1)混沌初始化。假設優化變量為D維。隨機生成D維向量z1=[z11,z12,…,z1D]，每個分量均處于[0,1]，依據Logistic方程獲得M個分量，z1,z2,…,zM：

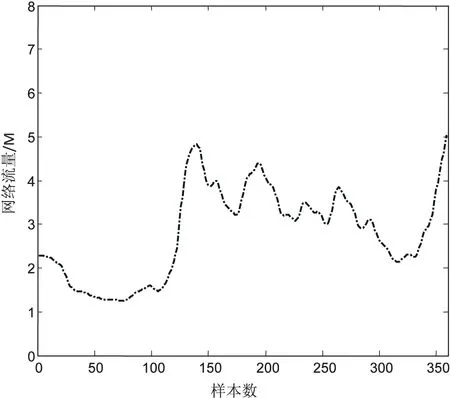
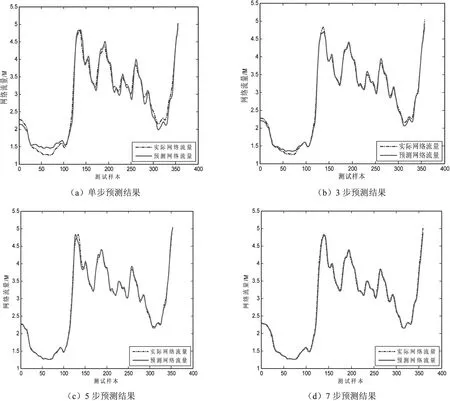
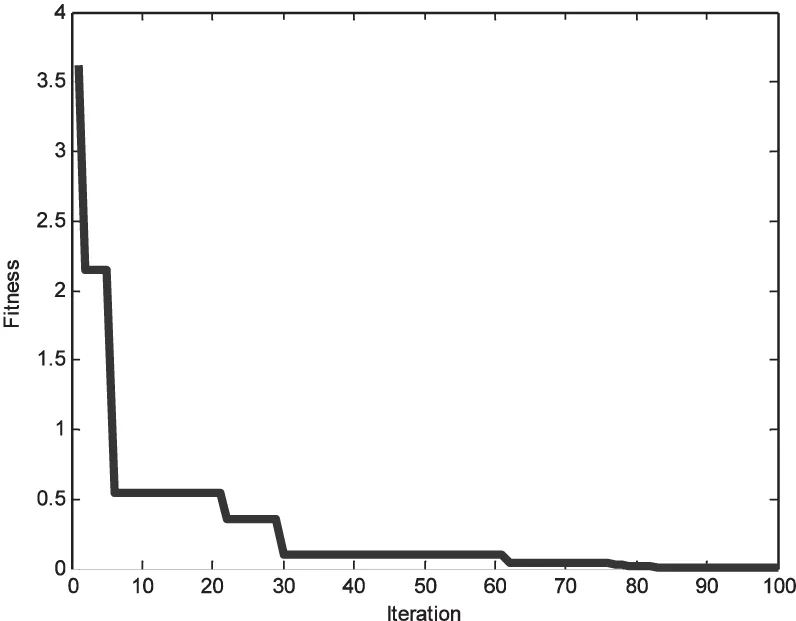
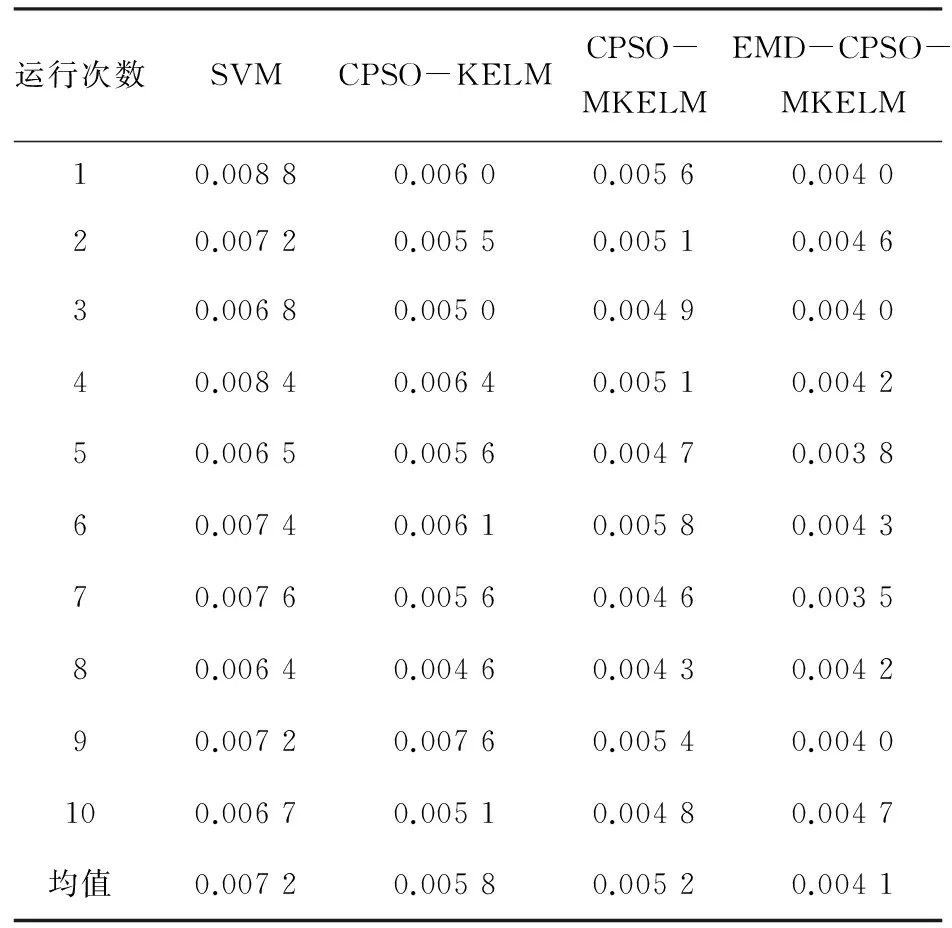
zn+1=μzn(1-zn),n=0,1,…;0

(13)

運用式(13)實現混沌區間和變量范圍的映射：

xij=aj+(bj-aj)zij

其中，bj,aj分別表示所需優化變量的上界和下界。

(2)依據適應度函數評估每個粒子的適應度函數值，從M個初始粒子群中選擇N個作為初始解，粒子的速度隨機生成。

(3)設定初始個體極值和全局極值。設定各粒子的當前位置為個體極值Pi，依據適應度函數評估各個體極值Pi的適應度函數值，選擇最優值的粒子所在位置定義為全局極值Pg。

(4)根據式(14)和式(15)實現粒子飛行速度和位置的更新。

(15)

(5)混沌優化最優位置Pg。先將最優位置映射成為Logistic方程的取值范圍[0,1]，再根據Logistic方程生成m個混沌變量序列，最后將生成的混沌變量序列映射到優化變量，獲得m個粒子，評估每個粒子的適應度函數值，獲得最優解p'。

(6)用最優解p'更新當前粒子搜索群體中任意粒子的位置。

(7)轉到步驟(4)，若粒子群終止條件滿足，則輸出最優結果；反之，繼續迭代。

2.4 混沌粒子群算法優化組合核極限學習機

需要優化的參數為組合核的權值p，高斯核的參數a，多項式核的參數q，以及懲罰因子C。

構造的適應度函數如下所示：

(16)

采用2.3所述算法進行優化，最終輸出4個參數的最優化結果。

3 仿真實驗

文中算法步驟如下：先采用EMD算法將時間序列分解成幾個分量，然后分別采用CPSO-MKELM進行預測，最后將各個預測結果進行相加組合重構出最終的預測結果。

3.1 數據來源

文中數據來源于流量文庫，收集自2014年11月7日—2014年11月21日一共15天的真實流量數據為研究對象，每天每間隔1小時采集一次網絡訪問流量，一共采集15*24=360組數據。網絡流量的原始網絡流量數據如圖1所示。

圖1 原始網絡流量

3.2 數據處理

對原始網絡流量數據序列進行EMD分解，依次分解出不同的IMF分量，網絡流量數據被分解成4個波動較小的分量和1個剩余分量。

針對每個分量采用時間序列的方法進行預測，以其中一個分量IMF1為例，采用IMF1(t-n)，IMF1(t-n+1),…,IMF1(t)來預測IMF1(t+1)。其中,n為時間序列預測的步長。

運用CPSO優化MKELM的模型分別對各個分量進行預測，最后通過各個分量的預測結果重構出網絡流量的預測結果。結果采用均方誤差來評價算法的性能。

3.3 實驗結果分析

將360組網絡流量數據分成訓練樣本和測試樣本，將336組數據作為訓練數據，后面24組作為測試數據，用于驗證預測結果的好壞。設定CPSO算法的最大迭代次數為100，種群大小為20，其預測結果如圖2所示，分別表示單步預測、3步預測、5步預測和7步預測。

圖2 基于EMD-CPSO-MKELM算法的7步網絡流量預測

由EMD-CPSO-MKELM算法的單步預測、3步預測、5步預測和7步預測結果圖可知，隨著預測步長的增加，EMD-CPSO-MKELM算法的預測精度不斷提高，效果較好。圖3是CPSO算法優化MKELM的適應度曲線。

圖3 CPSO優化MKELM的適應度曲線圖

為了對比EMD-CPSO-MKELM算法的優越性，將EMD-CPSO-MKELM算法、CPSO-MKELM算法、CPSO-KELM算法和普通的SVM算法四者的預測結果進行對比，運行10次，其對比結果如表1所示。

表1 四種算法預測的MSE誤差對比

從表1中可以看出，文中的多核極限學習機算法要好于普通的核極限學習機算法，同時由MSE誤差對比結果可知，文中的EMD-CPSO-MKELM算法的預測效果最好。

4 結束語

針對核極限學習機逼近能力的不足，文中提出了一種高斯核函數和多項式核函數加權組合的核極限學習機方法。針對該算法參數選擇對識別性能的影響，文中運用混沌粒子群算法對組合核極限學習機的核參數、權值以及懲罰因子進行優化，同時結合EMD提取網絡流量的細節特征和趨勢特征，構建出基于EMD-CPSO-MKELM的網絡流量預測模型，分別進行單步、3步、5步和7步預測。通過對比不同網絡流量預測模型的預測均方誤差發現，文中提出的算法預測精度要優于其他模型，從而為網絡資源的合理配置和可靠傳輸提供決策的依據。

[1] 雷 霆,余鎮危.一種網絡流量預測的小波神經網絡模型[J].計算機應用,2012,26(3):526-528.

[2] 楊 光,張國梅,劉星宇.基于小波核LS-SVM的網絡流量預測[J].微機發展(現更名：計算機技術與發展),2005,15(12):125-128.

[3] Huang G B,Zhu Q Y,Siew C K.Extreme learning machine:a new learning scheme of feedforward neural networks[J].Neurocomputing,2004,2(2):985-990.

[4] Huang G B,Ding X,Zhou H.Optimization method based extreme learning machine for classification[J].Neurocomputing,2010,74(1-3):155-163.

[5] 武峰雨,樂秀璠,南東亮.相空間重構的極端學習機短期風速預測模型[J].電力系統及其自動化學報,2013,25(1):136-141.

[6] 丁金林,王 峰,孫 洪,等.改進RELM在多變量解耦控制中的應用[J].微電子學與計算機,2012,29(11):70-73.

[7] 肖志勇,楊小玲,劉愛倫.基于改進EMD和LSSVM的機械故障診斷[J].自動化儀表,2008,29(6):24-26.

[8] 馮 平,丁志宏,韓瑞光,等.基于EMD的降雨徑流神經網絡預測模型[J].系統工程理論與實踐,2009,29(1):152-158.

[9] 徐曉剛,徐冠雷,王孝通,等.經驗模式分解(EMD)及其應用[J].電子學報,2009,37(3):581-585.

[10] 鄭志成，徐衛亞，徐 飛，等.基于混合核函數PSO-LSSVM的邊坡變形預測[J].巖土力學，2012,33(5)：1421-1426.

[11] Han Jianwei，Kamber M．數據挖掘概念與技術[M]．北京:機械工業出版社，2007．

[12] Freund Y，Schapire R E．A decision-theoretic generalization of on-line learning and an application to boosting[J]．Journal of Computer and System Sciences，1997，55(1):119-139．

[13] Moore A W，Zuev D．Internet traffic classification using Bayesian analysis techniques[C]//Proc of SIGMETRICS．[s.l.]:[s.n.],2005:50-60．

[14] 楊家海，吳建平，安常青．互聯網絡測量理論與應用[M].北京:人民郵電出版社，2009．

Network Flow Prediction Based on Optimization Combined Kernel Extreme Learning Machine

LIU Yue,WANG Fang

(College of Information Engineering,Kaifeng University,Kaifeng 475004,China)

In order to improve precision of network flow prediction,a prediction model is proposed in this paper based on Empirical Mode Decomposition (EMD) and chaos particle swarm optimization combined kernel extreme learning machine aiming at the features of non-linear and non-stationary for network flow data.Unit flow is obtained through EMD on the network flow in time sequence,then each unit data is predicted with kernel extreme learning machine.Finally,the prediction result is reconstructed.In view of the inadequate fitting capacity of traditional kernel extreme learning machine,a machine combining Gaussian kernel and multinomial kernel is proposed and the improved kernel parameter combination and penalty factor of chaos particle swarm optimization with combined kernel are applied in the prediction of network flow.The experiment shows that this method can improve the accuracy of network prediction effectively,and help guide the rational allocation and planning of network resources.

network flow prediction;kernel extreme learning machine;combined kernel function;chaos particle swarm;empirical mode decomposition

2015-10-01

2016-01-05

時間：2016-05-05

河南省教育科學技術研究重點項目(15C520016);開封市科技攻關計劃項目(130145)

劉 悅(1977-)，男，碩士，講師，研究方向為機器學習、網絡安全。

http://www.cnki.net/kcms/detail/61.1450.TP.20160505.0831.112.html

TP391.9

A

1673-629X(2016)06-0073-05

10.3969/j.issn.1673-629X.2016.06.016