直面學生的錯誤，促進知識的理解與內化

劉秀珍

[摘 要]隨著課程改革的深入實施，越來越多的教師認識到學生的錯誤是課堂中的重要教學資源。課堂教學中，教師只有直面學生的錯誤，有效利用錯誤資源，才能提高課堂教學的效率，夯實學生的學習基礎。

[關鍵詞]數學教學 錯誤 思維 算理 算法 技能 認知結構

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2016）05-023

錯誤，作為學生學習的必然產物，在學生的學習過程中是不可避免的；錯誤，作為學生學習的一種勞動成果，需要教師去關注、去尊重、去寬容。身為一線教師，課堂教學中，如何有效利用錯誤資源，提高學生的學習效率、提升教學質量及夯實學生的學習基礎呢？下面，我以“被減數的末尾有零的連續退位減法”教學為例，談談自己的一些做法。

片斷一：學生嘗試解答，呈現不同思維

出示例題：小明的媽媽帶了1000元錢，到商場買衣服花了736元，她還剩下多少錢？

（生讀題后列出算式：1000-736）

師：請同學們觀察算式中數字的特點，看看能發現什么。

生：被減數的末尾是零。

師：同學們會算嗎？（學生意見不一）試著用自己的方法算一算。（師巡視，收集學生的一些典型做法，如下）

思考：連續退位減法對于三年級學生來說，算理的理解和技能的掌握是有一定難度的，尤其是中間或末尾有零的連續退位減法，部分學生即使到了高年級還是會出錯。既然學生學習的難度很大，我們為什么不去教、不去講呢？設計嘗試計算這一環節的目的，就是為了充分展示每一位學生的認知情況，暴露學生的思維過程，并為學生后面的學習做適當的定向引導。

片斷二：找準知識“生長點”，操作理解算理

（1）組織小組交流。

出示交流要求：

①比一比，這兩種做法有什么相同的地方，有什么不同的地方？

②議一議，上面的做法正確嗎？被減數末尾有零的減法應該怎樣計算？

（2）集體反饋想法。

生1：我們小組交流后認為，這兩種做法的結果在個位上是相同的，在十位和百位上不相同；第二種做法是不對的，十位和百位上應該用9去減。

生2：我也認為第二種做法不對，但聽了同學們的想法后，我還是不太明白。

……

思考：學生交流的結果在教師預測的范圍之內。末尾有零的連續退位減法，在嘗試計算的過程中，部分學生只是大概覺得是這么做，事實上并沒有真正明白算理。設計本環節教學的目的，是為了使學生在交流的過程中明確自己思維混沌的地方，從而激發他們進一步探究的欲望。

（3）操作理解算理。

師：1000減去736，差的十位和百位上究竟是多少，部分同學不太明白，接下來我們用畫圖的方法來理解算理。

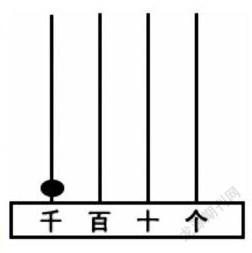
①如右圖，在計數器的千位上畫一個珠子表示1000。

師：1000減去736，被減數的個位、十位、百位上都是0，都不夠減，怎么辦？

生3：個位上0減6不夠減，向它的前一位十位去借；可是十位上也是0，只能向百位去借；可百位上還是0，只能向千位去借；千位上是1，正好可以借到。

師：從千位上借到1個后，百位、十位、個位可以退位成多少？請同學們分步在計數器上畫出來。

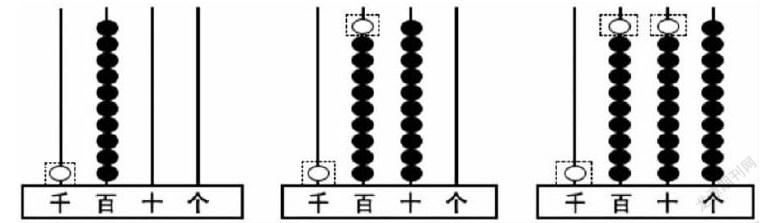
②投影展示學生的作品（如下）。

（結合圖例，學生講解退位的過程）

生4：千位上退一到百位，“借一當十”，所以百位上是10；百位上又退一到十位，這時百位上剩9，十位上是10；十位上又退一到個位，于是十位上剩9，個位上是10。

師：被減數的百位和十位上原來一個也沒有，當它們向前一位借到1變成10后，毫不吝嗇地從10中拿出1來借給它們右邊低一級的數位，真可謂是一個“慷慨的窮光蛋”！那么，1000減去736，差是多少？

生5：差是246。

……

思考：根據學生的年齡特點和認知需求，通過動手操作的方法，把操作和算理聯系起來，不僅有效地突破了教學難點，而且把學生作為操作的主體，讓學生親身經歷、親手操作，算理的理解自然會更清晰、更深刻。

片斷三：法理相融，掌握算法

師：請同學們結合前面的算理，重新用豎式計算出結果。

生： 1000

- 736

264

師：兩人一組，挑選其中一位同學說一說計算的過程。

師生小結計算方法：相同數位對齊，從個位減起。個位0減6不夠減，向十位借，十位和百位上都是0，向千位借。千位退一，千位是0，百位是10；百位又退一，百位剩9，十位是10；十位又退一，十位剩9，個位是10。個位10-6=4，十位9-3=6，百位9-7=2，千位是0不用寫，所以差是264。

……

思考：算理是計算的原理和根據，算法是計算的基本程序和方法。算理和算法是不可分割的一個整體，理解算理的過程實質上是為了促進算法的抽象。算理不清，算法難以牢固；算法不明，計算技能難以形成，所以教師教學中要及時引導學生抽象出算法。

片斷四：鞏固運算法則，提高運算技能

（1）針對性練習。

1000-432= 1010-432= 1001-432=

思考：學生獨立完成后反饋交流，師根據學生的典型錯例進行評析，使學生明確：被減數各位上的0，當它向前一位借1變成10后，如果要給它后面的一位借1，它是9；如果不需要給后面一位借1，它還是10。

（2）思維性練習。

課后反思：

1.操作理解算理，有效突破難點

新教材將“被減數的中間或末尾有零的連續退位減法”這一內容從二年級推后到三年級，究其原因，是因為學生對算理的理解有一定的難度。本節課，我把操作和算理的理解緊密聯系起來，讓學生在理解的“節點”上、在知識的“生長點”上親手操作，親身經歷知識的獲取過程，使學生不僅“識其貌”，而且“知其理”。

2.關注學生錯例，重組認知結構

本節課主要有三個環節，即允錯、融錯、改錯，我利用學生的典型錯例，激發學生的認知沖突，使學生的思維由混沌變得清晰，在積極思考中真正理解了所學知識。

（責編 杜 華）