減小雙軸旋轉慣導中陀螺儀隨機漂移影響的方法研究

姜 睿，楊功流，周 瀟

(北京航空航天大學 儀器科學與光電工程學院，北京 100191)

減小雙軸旋轉慣導中陀螺儀隨機漂移影響的方法研究

姜 睿，楊功流，周 瀟

(北京航空航天大學 儀器科學與光電工程學院，北京 100191)

針對雙軸旋轉慣導慣性器件的隨機誤差無法在導航過程中自動進行補償的問題，提出優化的兩位置重調(TPR)的方法來補償系統的隨機誤差導致的方位和位置誤差，以提高雙軸旋轉慣導的長航時精度。與傳統兩位置重調(CPR)方法相比，使用優化的誤差傳遞方程的兩位置重調的方法，可以在少于6h條件下估計出系統的方位誤差，從而使得系統的位置精度和方位精度都得以極大的提高。根據慣性器件的隨機誤差導致的方位誤差的特性，建立了TPR的誤差模型。通過仿真，證明了該方法的有效性。

兩位置重調；雙軸旋轉；隨機誤差

0 引言

雙軸旋轉慣導起源于旋轉式慣性單元技術[1]，該技術可以通過旋轉的方法在短期內平均慣性測量單元的漂移。雙軸旋轉慣導具有高精度和低成本的特點，因此廣泛地被北大西洋公約組織和美國用于海面艦艇和潛艇導航中[2-3]。很多研究都集中在如何提高雙軸旋轉慣導的精度。文獻[4]介紹了雙軸旋轉的轉位方案，自標定技術。文獻[5]提出了重調方法。文獻[6]給出了16位置旋轉方案，該旋轉方法可以補償所有陀螺儀的漂移并且不會引入其他累積的系統誤差。文獻[7]講解了包括誤差傳遞特性和轉位方案設計在內的雙軸旋轉慣導的關鍵技術。文獻[8]討論了雙軸旋轉慣導的轉動引起的誤差。

上面提到的技術和方法解決了很多雙軸旋轉慣導在實際應用中出現的問題。為了進一步提高精度，還需要對重調技術進行研究。對于普通的慣導，陀螺儀的隨機誤差將造成位置誤差和方位誤差，只有位置誤差可以通過傳統的重調技術(CPR)進行補償[9]。實際上，通過優化姿態誤差模型，位置誤差和方位誤差可以同時得到補償。本文在推導雙軸旋轉慣導誤差傳遞方程的基礎上，提出改進的兩位置重調的方法，用于在4～6h之間任何一點修正由陀螺隨機漂移引起的方位誤差和位置誤差，并且根據提出的方案進行了仿真驗證。

1 雙軸旋轉慣導的誤差建模

雙軸旋轉慣導仍然屬于捷聯式慣導的范疇，因此其誤差方程和捷聯式慣導的誤差方程總體上是一樣的[10]。誤差傳遞方程的推導有兩種途徑：ψ角誤差模型和Ф角誤差模型[11-12]。本文使用ψ角誤差模型來描述雙軸旋轉慣導誤差傳遞特性。

(1)

(2)

(3)

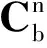
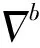
εb=bg+Sgωb+Ngωb+Kgfb+νg

(4)

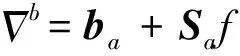
(5)

式中，bg為陀螺常值偏置 ，ba為加速度計比例偏置，Sg為陀螺儀比例因素誤差矩陣，Sa為加速度計比例因素誤差矩陣，Ng、Na為不對準誤差矩陣，Kg代表與g有關項偏移系數矩陣。fb是作用在載體坐標系下的外力。νg、νa是隨機誤差。載體坐標系是正交坐標系，陀螺儀坐標系與載體坐標系之間關系如圖1所示。

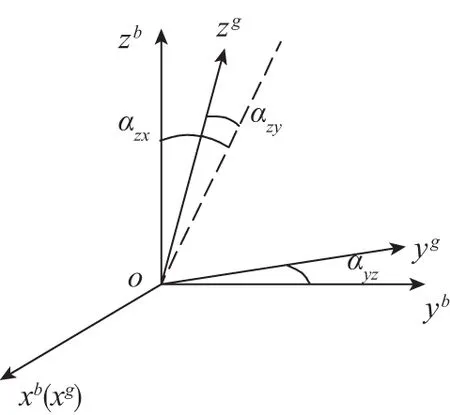
圖1 載體坐標系與陀螺儀坐標系之間的關系Fig.1 Relationship between the body frame (b frame) and the gyro frame(s frame)

xb與xg一致，yb在ygxg平面內，zb與xb、yb滿足右手定則。

由于不對準角是小角，陀螺儀的不對準誤差矩陣可以寫為

(6)

同樣，加速度計敏感軸與陀螺儀敏感軸之間的不對準誤差矩陣可以寫為[7]

(7)

2 兩位置重調

重調(PR)是船用慣導系統特有的一項關鍵技術，借助準確的外界輔助信息(如衛星定位信息、天文導航姿態信息等)對慣導系統誤差進行修正。重調期間，需要提供位置信息才可以進行慣導系統相關參數的校正。雖然陀螺儀的隨機誤差會引起方位誤差和位置誤差，但通常在傳統的重調方法(CPR)中會忽略方位誤差[10]。

本節將研究陀螺儀隨機漂移引起的方位誤差，并提供用于雙軸旋轉慣導隨機誤差補償的兩位置重調的方法。與傳統的位置重調法相比，兩位置重調可以同時估計和補償方位誤差和位置誤差。

2.1 陀螺儀隨機漂移引入的方位誤差的特性

在第1節中提到，慣導誤差傳遞方程有兩種表達方法，一種基于ψ角，一種基于Ф角。兩者之間的關系如下[8]

Φn=δθn+ψn

(8)

其中，Φn是Φ角誤差，ψn是ψ角誤差。δθn是位置角誤差，可用式(9)表達為

(9)

式中，L為當地緯度，δL為緯度誤差，δλ為經度誤差。

與g有關項偏置，比例因數誤差和不對準誤差等常值誤差可以通過標定確定[11-15]。則傳感器的誤差模型可以簡化為:

(10)

由雙軸旋轉慣導的原理[3,5]可知，式(4)和式(5)中的bg和ba兩項會被調制平均，所以在雙軸旋轉慣導中，陀螺儀的隨機漂移成為主要的誤差源。式(1)可以改寫為式(11)。

(11)

陸上、海面和水下載體都是長時間的導航，能達到幾天甚至幾個月以上，通常使用速度阻尼的方法減少舒勒周期對導航誤差的影響。橫搖角和縱搖角誤差能得到很大程度的降低[16]。但是，速度阻尼卻不能有效地減小方位角誤差。

2.2 兩位置重調的方法

為了估計和修正方位角誤差以及由隨機誤差引入的位置誤差，提出一個優化的重調方法，即兩位置重調。該方法包含兩步:

1)在第一個位置信息可用的時候，重置系統的位置；

2)估計并修正方位誤差直到第二次位置信息可用的時候，并重置位置信息。

兩位置重調的具體方法如下:

(12)

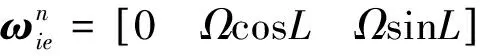
(13)

通常，陀螺儀的隨機誤差將緩慢地、累積性地影響在特征周期(T0=24h)中的ψ角的傳遞特性。因此，對于雙軸旋轉慣導系統，在陀螺常值漂移誤差被調制掉后，需要校正由陀螺儀的隨機誤差引起的位置和方位誤差。典型的ψ角誤差中方位角誤差的增長如圖2所示。

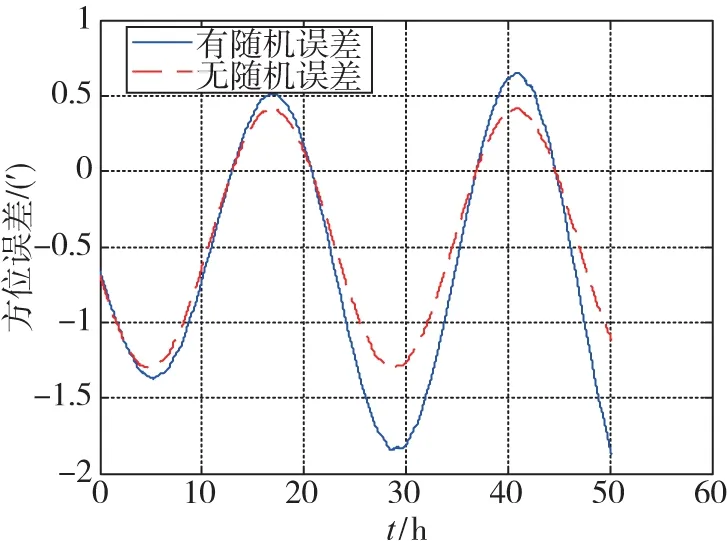
圖2 ψ角方位誤差的傳遞特性Fig.2 Propagation characteristic of an azimuth error of the psi-angle

在兩次重調之間有4～6h(傳統重調是6h)，比特征周期短了很多，由隨機誤差引起的誤差累積很小。因此，在兩次重調之間，可以用不包含隨機誤差的方位誤差曲線擬合包含隨機誤差的方位誤差曲線，擬合精度在短時間內是滿足要求的。

根據含有隨機誤差的式(12)，不含隨機誤差的式(14)如下

(14)

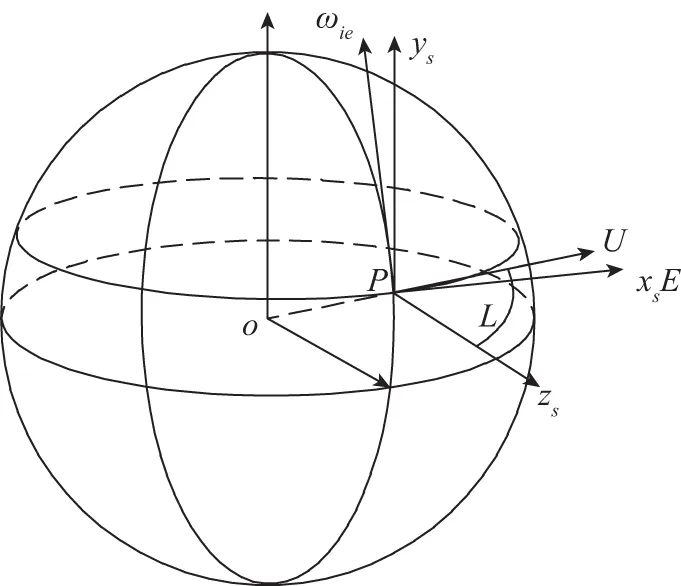
圖3 S坐標系與導航坐標系之間的關系Fig.3 Relationship between the gyro frame(S frame) and the navigation frame

S坐標系到導航坐標系n的方向余弦矩陣是

(15)

則S坐標系下的ψ角可以表示為

(16)

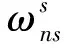
(17)

式(17)的解析解為

ψt(t)=T(t,t0)·ψs(t0)

(18)

其中

(19)

由于速度阻尼能顯著地減小縱搖角和橫搖角的誤差，以在兩次重調期間，縱搖角和橫搖角的誤差接近于零。因此式(8)可以簡化為：

(20)

將式(8)、式(9)和式(17)帶到式(20)中得到

(21)

根據第一個位置的信息，式(18)可以重新編輯作為第一次重調的式(22)

(22)

同理，第二次重調時經緯度誤差和方位角為

(23)

因此，兩個重調點之間的關系為:

(24)

需要注意的是，這里有三個假設條件：

1)縱搖角誤差和橫搖角誤差為零；

2)陀螺儀的常值偏移誤差經過調制；

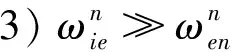
實際上，在整個重調期間，這些假設不是都能成立。但是在低速和小機動的情況下，兩位置重調可以估計出滿足使用的方位誤差。通過仿真可以驗證這一點。

3 兩位置重調的仿真計算

為了證明所提出的兩位置重調方法的優勢，將傳統重調也同時進行仿真以作為比對。仿真條件如下:

1)初始對準姿態誤差(0′,0′,1.8′)；

3)兩次重調分別在第20個小時和第26個小時；

4)系統的導航過程中有速度阻尼。

仿真結果如圖4和圖5所示。圖4是在速度阻尼的情況下進行兩位置重調和傳統重調時方位誤差的比對圖。圖5是在速度阻尼的情況下進行兩位置重調和傳統重調時位置誤差的比對圖。兩個方法都在第20個小時對位置誤差進行修正。在第26個小時，包含ψ角誤差和位置誤差的方位誤差(φ角誤差)通過兩位置重調得到補償，而傳統的重調只補償了位置誤差。

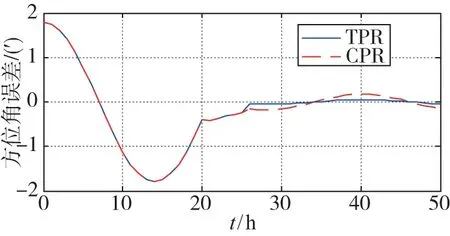
圖4 傳統重調和兩位置重調方位誤差Fig.4 Azimuth errors by using the TPR method and by using the CPR

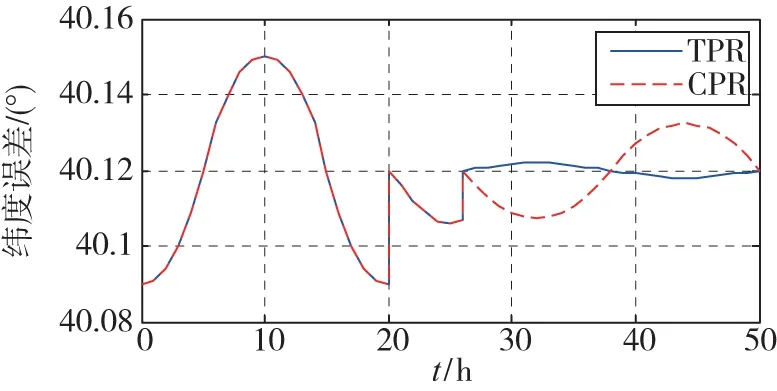
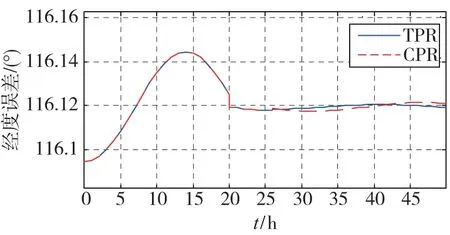
圖5 速度阻尼下兩種方法經度和緯度誤差對比Fig.5 Latitude and lontitde error with velocity damping by using the TPR method and by using the CPR method

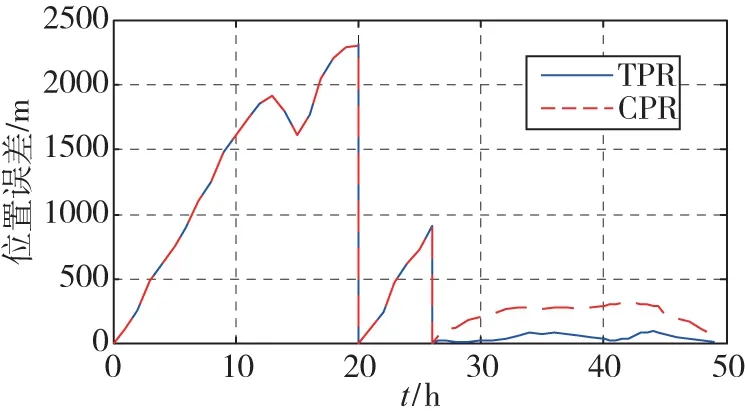
圖6 速度阻尼下兩種方法位置誤差對比圖Fig.6 Position output with velocity damping by using the TPR method and by using the CPR method

圖6是有速度阻尼時，傳統重調和兩位置重調下的位置圓概率誤差對比圖。從圖6中可以看出，使用兩位置重調，位置圓概率誤差小于90m。使用傳統重調，位置圓概率誤差大于300m。

根據上面的對比可以得到這樣的結論，在相同的仿真條件下，使用兩位置重調時，方位誤差和位置圓概率誤差都優于傳統的重調方法。

4 結論

為了提高雙軸旋轉慣導在長航時的系統精度，降低陀螺儀隨機游走對位置精度的影響，本文提出了兩位置重調的方法。該方法在以下方面取得了明顯的效果：

1)利用兩點位置信息，同時修正慣導系統位置誤差和方位誤差；

2)由于方位誤差是通過計算公式估計，因此兩位置修正時間間隔不受6h限制，一般選擇4～6h，極大地提高了艦艇的安全。

[1]FinckeWH.StrapdownInertialSensingUnitRotation/SISUR/-Anewapproachtoinertialnavigation[C]//IEEE1978PositionLocationandNavigationSymposium, 1978: 132-145.

[2]TittertonD,WestonJL.Strapdowninertialnavigationtechnology[M].IET, 2004.

[3]LevinsonE,MajureR.Accuracyenhancementtechniquesappliedtothemarineringlaserinertialnavigator(MARLIN)[J].Navigation, 1987, 34(1): 64-86.

[4]LevinsonE,GiovanniCS.Lasergyropotentialforlongendurancemarinenavigation[C]//IEEEPositionLocationandNavigationSymposium, 1980: 115 -129.

[5]YuanB,LiaoD,HanS.ErrorcompensationofanopticalgyroINSbymulti-axisrotation[J].MeasurementScienceandTechnology, 2012, 23(2): 025102.

[6]YinH,YangG,SongN,etal.Errormodulationschemeanalyzingfordual-axisrotatingfiber-opticgyroinertialnavigationsystem[J].SensorLetters, 2012, 10(7): 1359-1363.

[7]SongN,CaiQ,YangG,etal.Analysisandcalibrationofthemountingerrorsbetweeninertialmeasurementunitandturntableindual-axisrotationalinertialnavigationsystem[J].MeasurementScienceandTechnology, 2013, 24(11): 115002.

[8]Goshen-MeskinD,Bar-ItzhackIY.Unifiedapproachtoinertialnavigationsystemerrormodeling[J].JournalofGuidance,Control,andDynamics, 1992, 15(3): 648-653.

[9]BensonJrDO.Acomparisonoftwoapproachestopure-inertialandDoppler-inertialerroranalysis[J].AerospaceandElectronicSystems,IEEETransactionson, 1975 (4): 447-455.

[10]BonaBE,SmayRJ.Optimumresetofship'sinertialnavigationsystem[J].AerospaceandElectronicSystems,IEEETransactionson, 1966,2(4): 409-414.

[11]SyedZF,AggarwalP,GoodallC,etal.Anewmulti-positioncalibrationmethodforMEMSinertialnavigationsystems[J].MeasurementScienceandTechnology, 2007, 18(7): 1897.

[12]NieminenT,KangasJ,SuuriniemiS,etal.Anenhancedmulti-positioncalibrationmethodforconsumer-gradeinertialmeasurementunitsappliedandtested[J].MeasurementScienceandTechnology, 2010, 21(10): 105204.

[13]FongWT,OngSK,NeeAYC.Methodsforin-fieldusercalibrationofaninertialmeasurementunitwithoutexternalequipment[J].MeasurementScienceandTechnology, 2008, 19(8): 085202.

[14]ZhangH,WuY,WuW,etal.Improvedmulti-positioncalibrationforinertialmeasurementunits[J].MeasurementScienceandTechnology, 2009, 21(1): 015107.

[15]LiY,NiuX,ZhangQ,etal.Aninsituhandcalibrationmethodusingapseudo-observationschemeforlow-endinertialmeasurementunits[J].MeasurementScienceandTechnology, 2012, 23(10): 105104.

[16] 高鐘毓. 慣性導航系統技術[M]. 北京：清華大學出版社, 2012.

Research on Reducing the Influence of Stochastic Error of Gyros in a Dual-Axis Rotational Inertial Navigation System

JIANG Rui,YANG Gong-liu,ZHOU Xiao

(School of Instrumentation Science and Opto-electronics Engineering, Beihang University, Beijing 100191, China)

The stochastic errors of inertial sensors in a dual-axis rotational inertial navigation system are not averaged out automatically during navigation. Therefore an optimized Twice Position-fix Reset (TPR) method is provided to enhance accuracy of a dual-axis rotational INS by compensating stochastic errors. Compared with Conventional Position-fix Reset(CPR) method, both an azimuth error and a radial-position error are extremely corrected within 6 hours by the TPR method. An optimized error propagation equation has built on the characteristics of an azimuth error introduced by stochastic errors of an inertial sensor. As the result, accuracy of the system is prominently enhanced, as is verified by simulation.

Twice position-fix reset; Dual-axis rotation; Stochastic error

10.19306/j.cnki.2095-8110.2016.04.005

2016-04-20；

2016-05-23。

姜睿(1975-)，女，碩士，主要從事慣性技術的研究。E-mail：Buaajr@163.com

U666.1

A

2095-8110(2016)04-0025-05