基于相空間重構的神經網絡風暴潮增水預測方法

尤成，于福江，原野

（國家海洋環境預報中心國家海洋局海洋災害預報技術研究重點實驗室，北京100081）

?

基于相空間重構的神經網絡風暴潮增水預測方法

尤成，于福江，原野

（國家海洋環境預報中心國家海洋局海洋災害預報技術研究重點實驗室，北京100081）

摘要：風暴潮增水的準確預測對于國民生產、防災減災有重大意義。本文提出一種基于相空間重構的神經網絡風暴潮增水預測方法，即使用單站風暴潮增水數據重構出與之相關的相空間，然后使用BP神經網絡模型擬合該相空間的空間結構。將該模型用于庫克斯港風暴潮增水預測,結果表明：該模型應用在風暴潮增水時間序列的預測中是合理、可行的,并具有較高的精度。此外，使用db10小波函數對原始余水位數據進行降噪處理可以顯著地提高模型的預測精度。

關鍵詞：相空間重構；BP神經網絡；風暴潮增水預測；小波降噪

1　引言

Packard等[1]提出了重構相空間的思想。隨后Takens等[2]提出嵌入定理，建立起觀測資料與動力系統空間特征之間的橋梁，使得深入分析時間序列的背景和動力學機制成為可能。Lyapunov指數、G-P關聯維算法、虛假近鄰法、Cao方法、自相關法、互信息法、C-C方法等對各種參數的計算，使得相空間重構技術日趨成熟。Farmer等[3]第一次提出使用相空間重構的方法預測時間序列。這個方法后來被稱作k-NN方法。許多學者討論K-NN方法中權重系數ωi該如何取值[4-6]。為了盡量避免k的選取引起預測誤差，Yankov等[7]以一組k取值不同的k-NN方法為成員，進行集合預報，發現預報效果有一定的改進。此外，人們在天氣預報、水文預報等方面應用相空間重構的理論進行了研究取得了相當的成果。張穎超和劉玉珠[8]研究表明：基于相空間重構的神經網絡短期氣候預測方法有合理的精度，可以為短期氣候預測提供參考。Solomatine等[9]使用單變量局域方法預測風暴潮，結果表明其預報精度明顯好于AR、ARIMA等線性模型。Velickov[10]進一步使用多變量局域方法來預測風暴潮，結果表明這種預測方法短期預報結果可以信賴。Siek等[11]使用PCA方法降低數據維度，提高了預報精度。Siek等[12]比較單變量k-NN方法、多變量k-NN方法以及神經網絡模型的預報風暴潮增水的效果，結果表明：k-NN方法與神經網絡模型有相當的預報精度，但k-NN方法預報極端事件的能力更強，此外與單變量k-NN方法相比，多變量k-NN方法在預報精度上并沒有明顯的改進。但是K-NN方法在尋找臨近點時，經常把相空間中臨近時刻的點當作臨近點，使得預報結果精度降低。為了規避K-NN方法的這一缺陷，本文使用相空間重構與BP神經網絡相結合的方法來預測風暴潮增水，并給出了該方法的最大預測期限。

2　基本原理和方法

2.1相空間重構

根據Takens的嵌入定理[2]，在無噪聲情況下，觀察到的時間序列{xn}以向量

Xn=(xn,xn-τ,…,xn-(m-1)τ)（1）

的形式形成m維空間，只要嵌入維數m≥2d+1，動力系統的幾何結構可以完全打開，其中d是吸引子的分形維數，τ是延遲時間間隔。條件m≥2d+1是動力系統重構的充分不必要條件。狀態空間Rm中吸引子的幾何特征與原動力系統的幾何特征等價，并且狀態空間中Xn→Xn+1的演化反映了原動力系統的演化特征。類似于Takens的嵌入定理，只要嵌入維數充分大，存在映射G:Rm→Rm使得

Xn+1=G(Xn)[13]（2）

本文使用BP神經網絡來擬合G(·)。

2.2 BP神經網絡的基本原理

BP神經網絡全稱是誤差反向傳播神經網絡（Back Propagation）。它具有結構簡單、工作狀態穩定、易于硬件實現等優點。BP算法通過輸入、輸出數據樣本集，根據誤差反向傳遞的原理對網絡進行訓練。其學習過程包括信號的正向傳播和誤差的反向傳播兩個階段。

正向傳播中輸入信息從輸入層經隱層逐層計算各單位輸出值：

對輸出層：

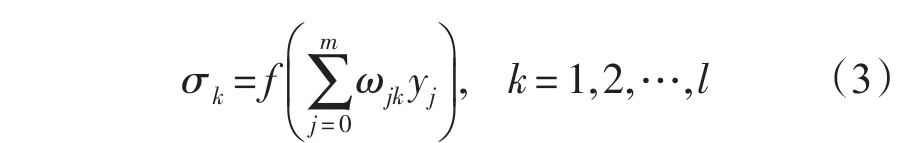
對隱藏層：

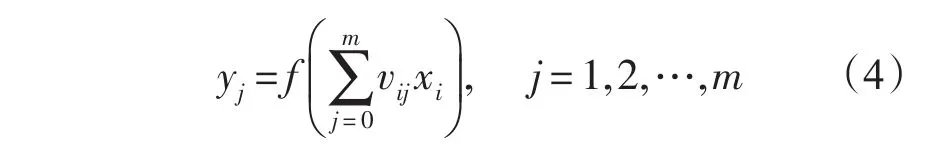
式中：xi表示輸入層節點，σk是隱藏層節點，yj表示輸出層節點，vij是輸出層到隱藏層之間的權重，ωjk是隱藏層到輸出層之間的權重。

反向傳播過程中輸出誤差的同時，逐層向前算出隱層各個單元的誤差，并以此誤差修正前層的值。直到誤差達到要求，網絡學習過程結束。

2.3相空間重構與BP神經網絡相結合的風暴潮增

水預測方法

相空間重構理論和神經網絡有2個結合點[8]，首先它們都適合處理非線性復雜系統問題；其次，根據相空間重構預測模型式（3），可以發揮神經網絡自適應、自學習的特點，選擇訓練樣本訓練神經網絡，模擬G(·)，從而進行預測。具體步驟如下：

第一步：收集驗潮站的潮位數據并減去潮汐部分，得到逐小時的余水位數據{xi, i=1,2,...,n}；

第二步：使用db10小波對余水位數據進行降噪；

第四步：建立神經網絡，每個輸入數據之間時間相差τ個時間點，即將xn,xn-τ,…,xn-(m-1)τ作為神經網絡的輸入。輸出為預測時間點的預測值，即xn+1；

第五步：訓練神經網絡，在確定網格的輸入輸出結構后，選擇學習樣本構成訓練集，對網格進行訓練，直到達到誤差要求為止；

第六步：網絡訓練成功后，選取預測時間點，應用前面建立的模型進行預測。

3　算例分析與討論

北海地區，尤其是荷蘭、丹麥以及德國北部沿海地區特別容易受到風暴潮的侵襲。庫克斯港位于黑爾戈蘭灣內，易北河河口處，是一座重要的漁業港口。本文選取庫克斯港1981年1月1日—1983 年12月20日的逐小時潮位數據進行相空間重構以及神經網絡訓練，使用1983年12月21日—1984年1月23日的逐小時潮位數據進行驗證。冬季是北海地區風暴潮頻發的季節，僅1983年12月21日—1984年1月23日就有6次增水超過1 m的風暴潮過程，以及一次較強的減水過程。其中最劇烈的一次風暴潮過程引起了將近2 m的增水。

3.1數據處理

首先使用t_tide潮汐分析工具包從庫克斯港潮位數據中提取潮汐信號，然后從潮位數據中減去潮汐部分得到逐小時的余水位時間序列。根據史珍等[14]研究表明：數值較大的高頻噪音對混沌系統的可預報性有顯著的影響。所以本文使用db10小波函數對余水位數據進行降噪處理。圖1表明降噪之后的余水位數據基本上保留了原始余水位中風暴潮增水的信息。

3.2風暴潮增水時間序列的相空間重構

相空間重構的關鍵是參數的選擇，Fraser等[15]提出利用互信息函數的第一極小值來確定延遲時間t。本文使用楊志安等[16]提出的等間距分格子法來計算互信息函數并以此確定延遲時間。計算結果見圖1。從圖1中可以看出無論把時間序列的值域等分成300份、400份、500份或600份，互信息都在t=7處取得第一最小值。本文采用Cao[17]提出的方法計算嵌入維數m，計算結果見圖2。從圖2中可以看出當嵌入維數m大于或等于9時，E1沒有顯著變化。于是取m=9。

3.3 BP網絡設計

采用BP神經網絡進行預測時，網絡輸入層神經元為10個，輸出層神經元為10個。為了避免因為數據間數量級差別而造成網絡預測誤差較大，首先對輸入輸出數據進行歸一化處理，將數據轉化為[0,1]區間的值，這里采用如下歸一化公式：

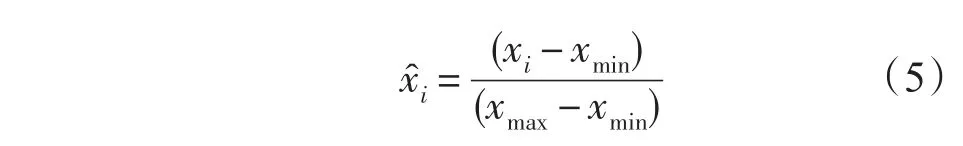
圖1　1981年10月3日—12月7日逐小時余水位數據及其降噪之后的數據

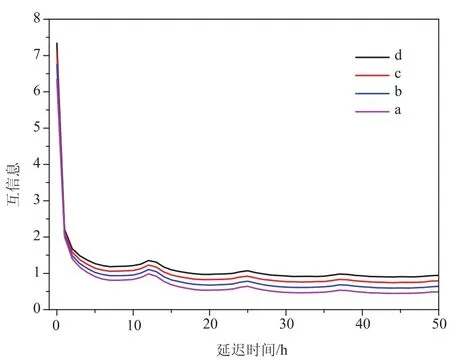
圖2　將時間序列的值域分別等分成300份（線a）、400份（線b）、500份（線c）以及600份（線d），求得的互信息與延遲時間的函數圖

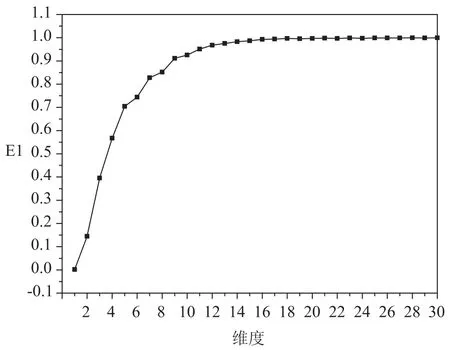
圖3　E1與維度的函數圖

3.4預測結果分析

本文選取庫克斯港1981年1月1日—1983年12月20日降噪之后逐小時余水位數據進行相空間重構以及神經網絡訓練。圖4給出了庫克斯港1983年12月21日—1984年1月23日余水位3 h預報值，及其預測誤差。從圖中可以看出：預測值與觀測值對應得很好，并且預測誤差基本上控制在± 6 cm以內。由此可見：基于相空間重構的BP神經網絡模型能較好地反映該序列內在的運動機理，揭示動力系統復雜的運動規律和非線性特征。此外，從表1可以看出：使用降噪之后的數據，可以明顯提高該模型的預測精度。

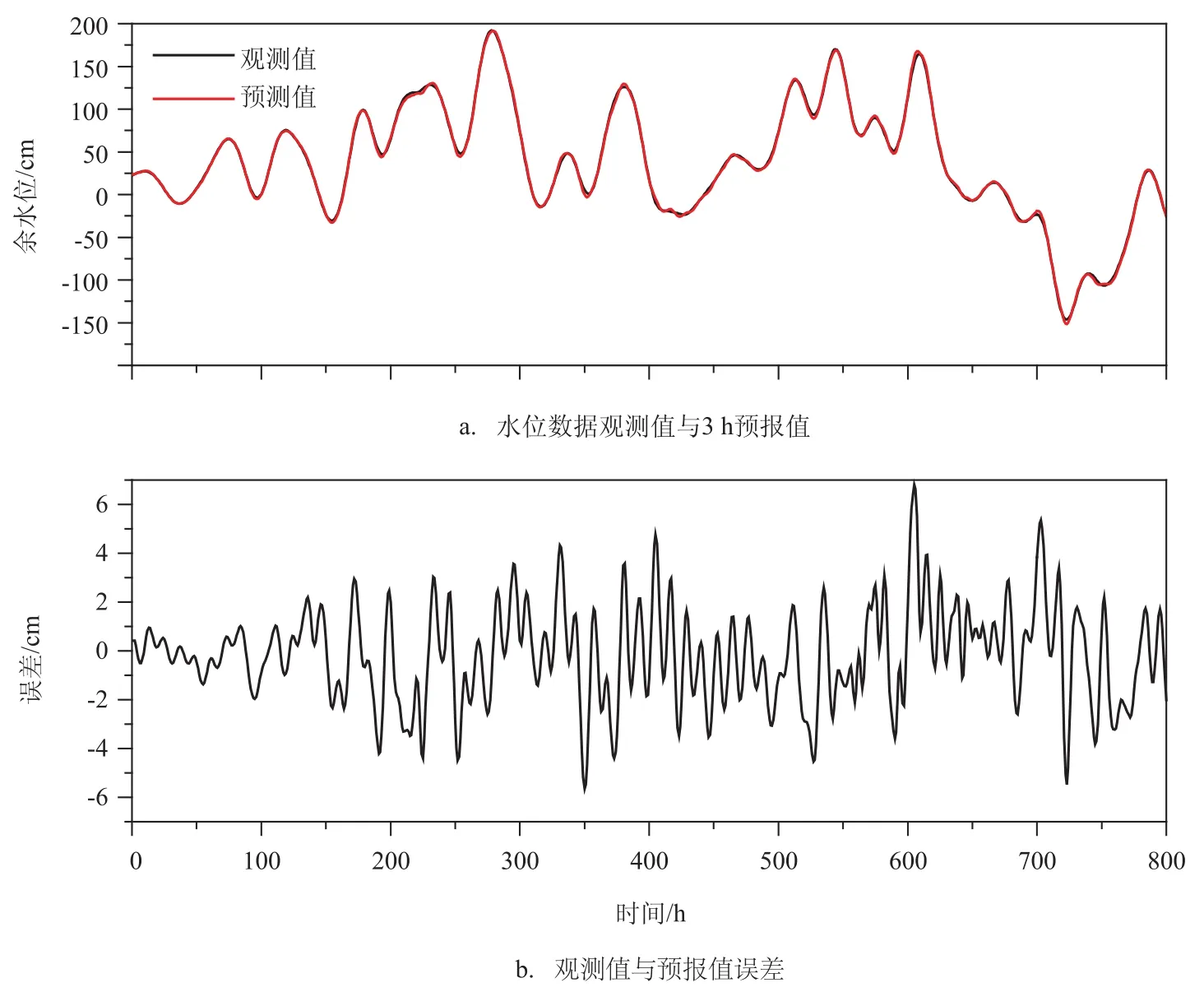
圖4　1983年12月21日—1984年1月23日庫克斯港逐小時余水位數據與誤差

表1　基于原始和降噪之后的余水位數據模型，1983年12月21日—1984年1月23日庫克斯港預報值對應的平均絕對誤差

3.5模型最大預測時限估計

為了定量地估計該方法的最大預測時限，本文根據Chen等[18]提出的具體算法來計算非線性Lyapunov指數（NLLE）。1 h預測值xi與其對應的真實值x'i的差的絕對值為，t時刻之后絕對誤差為，大量平均計算得到的NLLE為，絕對誤差。根據丁瑞強等[19]的研究表明：當t達到一定時刻，誤差達到飽和，系統的初始信息丟失，預測失去意義，于是最大預測期限可以定量地確定。實際操作時，把ln(err(t))達到飽和值的98%時的t當作相空間的最大預測期限。

計算結果（見圖5）表明基于相空間重構的神經網絡風暴潮增水預測方法在庫克斯港站的最大預測期限是26 h。

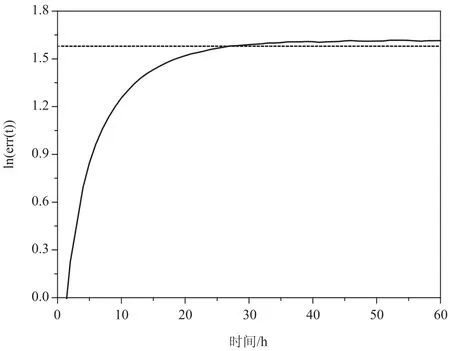
圖5　預測誤差的自然對數與預測時間的函數圖（水平虛線：誤差飽和值的98%）

4　結論

本研究使用單站風暴潮增水數據重構出與之相關的相空間，并使用BP神經網絡模型擬合該相空間的空間結構以便用于余水位預測研究。結果表明：

（1）基于相空間重構的BP神經網絡模型在風暴潮增水的短期預測中表現出良好的預測能力，這表明該模型能較好地反映該序列內在的運動機理，揭示動力系統復雜的運動規律和非線性特性；

（2）使用db10小波對原始余水位數據降噪之后可以顯著地提高模型的預測精度；

（3）利用非線性Lyapunov指數計算出基于相空間重構的神經網絡風暴潮增水預測方法在庫克斯港站的最大預測期限是26 h。

參考文獻：

[1] Packard N H, Crutchfield J P, Farmer J D, et al. Geometry from a time series[J]. Physical Review Letters, 1980, 45(9): 712-716.

[2] Takens F. Detecting strange attractors in turbulence[M]//Rand D, Young L S. Dynamical Systems and Turbulence, Warwick. Berlin Heidelberg: Springer, 1981: 366-381.

[3] Farmer J D, Sidorowich J J. Predicting chaotic time series[J]. Physical Review Letters, 1987, 59(8): 845-848.

[4]吳耿鋒,周佩玲,儲閱春,等.基于相空間重構的預測方法及其在天氣預報中的應用[J].自然雜志, 1999, 21(2): 107-110.

[5] McNames J, Suykens J A K, Vandewalle J. Winning entry of the K. U. Leuven time-series prediction competition[J]. International Journal of Bifurcation and Chaos, 1999, 9(8): 1485-1500.

[6]向小東,郭耀煌.基于混沌吸引子的時間序列預測方法及其應用[J].西南交通大學學報, 2001, 36(5): 472-475.

[7] Yankov D, DeCoste D, Keogh E. Ensembles of nearest neighbor forecasts[M]//Fürnkranz J, Scheffer T, Spiliopoulou M. Machine Learning: ECML 2006. Berlin Heidelberg: Springer, 2006: 545-556.

[8]張穎超,劉玉珠.基于相空間重構的神經網絡月降水量預測方法[J].計算機仿真, 2014, 31(1): 352-355.

[9] Solomatine D P, Rojas C J, Velickov S, et al. Chaos theory in predicting surge water levels in the North Sea[C]//Proceedings of the 4th International Conference on Hydroinformatics. Iowa, USA, 2000.

[10] Velickov S. Nonlinear dynamics and chaos with applications to hydrodynamics and hydrological modelling[M]. CRC Press, 2004.

[11] Siek M, Solomatine D, Velickov S. Multivariate chaotic models vs neural networks in predicting storm surge dynamics[C]// Proceedings of IEEE International Joint Conference on Neural Networks, 2008. IJCNN 2008. Hong Kong: IEEE, 2008: 2112-2119.

[12] Siek M, Solomatine D P. Nonlinear chaotic model for predicting storm surges[J]. Nonlinear Processes in Geophysics, 2010, 17(5): 405-420.

[13]王海燕,盧山.非線性時間序列分析及其應用[M].北京:科學出版社, 2006.

[14]史珍,丁瑞強,李建平.隨機誤差對混沌系統可預報性的影響[J].大氣科學, 2012, 36(3): 458-470.

[15] Fraser A M, Swinney H L. Independent coordinates for strange attractors from mutual information[J]. Physical Review A, 1986, 33(2): 1134-1140.

[16]楊志安,王光瑞,陳式剛.用等間距分格子法計算互信息函數確定延遲時間[J].計算物理, 1995, 12(4): 442-448.

[17] Cao L Y. Practical method for determining the minimum embedding dimension of a scalar time series[J]. Physica D: Nonlinear Phenomena, 1997, 110(1-2): 43-50.

[18] Chen B H, Li J P, Ding R Q. Nonlinear local Lyapunov exponent and atmospheric predictability research[J]. Science in China Series D: Earth Sciences, 2006, 49(10): 1111-1120.

[19]丁瑞強,李建平.誤差非線性的增長理論及可預報性研究[J].大氣科學, 2007, 31(4): 571-576.

Storm surge prediction method of neural network based on phase space reconstruction

YOU Cheng, YU Fu-jiang, YUAN Ye
(Key Laboratory of Research on Marine Hazards Forecasting, National Marine Environmental Forecasting Center, Beijing 100081 China)

Abstract：Accurate prediction of storm surge is significantly meaningful to the national production and disaster prevention and mitigation. The storm surge prediction model of BP neural network based on phase space was purposed in this paper, through combining reconstruction phase space with BP neural network. A phase space is reconstructed with the storm surge data and fitted with BP neural network model. The model is used to predict storm surge in Cuxhaven. The result of calculation shows the model is feasible, reasonable and highly precise. The prediction accuracy can been markedly improved through data de-noising.

Key words：phase space reconstruction; BP neural network; storm surge prediction; wavelet de-noising

作者簡介：尤成（1990-），男，碩士，主要從事基于相空間重構的預測方法研究。E-mail: puguan@yeah.net

基金項目：杭州灣海洋災害精細化預報系統（2013BAB04B02）。

收稿日期：2015-01-16

中圖分類號：P731.23

文獻標識碼：A

文章編號：1003-0239（2016）01-0059-06