有準備地建構模型

江蘇張家港市教育局教學研究室（215600）趙紅婷

?

有準備地建構模型

江蘇張家港市教育局教學研究室（215600）趙紅婷

［摘要］建模教學，對學生數學素養的形成具有重要意義。在學生參與準備教學資源后，教師再引領其經歷一個由繁趨簡的建模過程，這樣不但可以找尋數學知識的生長點，亦能促使學生有準備地建構數學模型。

［關鍵詞］備學建模

在執教蘇教版五年級下冊的“分數的意義”之前，我設計了幾個備學問題：

1．關于分數，你已經知道了什么？（至少寫出三點）

2．用分數表示圖中的涂色部分，并寫出每幅圖中分數的具體含義。

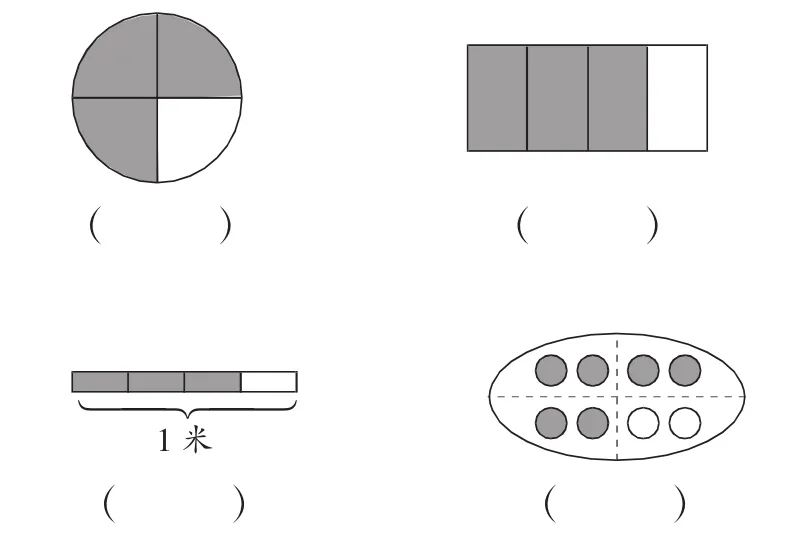
3．請提出關于分數的三個問題，并與小組的同學進行討論。

課始，學生匯報了自己關于分數的認識，回顧了分數各部分的名稱，并說出了各部分的含義。顯然，學生對分數并不陌生。有些學生在備學中還寫出了一些即將學習的新內容。

隨著對備學作業中第2個問題交流的深入，新知的學習也緩緩展開。

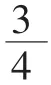
我引導學生明確：可以把一個物體平均分，也可以把一個計數單位平均分，還可以把由許多物體組成的一個整體平均分。

教師問：“這樣的例子有多少個？”

學生齊答：“無數個！”

教師追問：“可以用一句話概括這些例子嗎？”

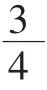
這種濃縮、精練的概括，只有數學抽象才能實現。數學的學習，便是要引導學生經歷這樣一個由繁趨簡的過程，這個過程無疑也是一個建模的過程。

還有學生說：“幾份就是若干份。”

南京大學鄭毓信教授指出：“數學是一種模式的科學。”

張奠宙教授解釋道：“廣義地講，數學中各種基本概念和基本算法，都可以叫做數學模型。狹義地講，只有那些反映特定問題或特定的具體事物的系統和數學關系結構才叫做數學模型。”

建模，對于數學學習有著重要意義。學生參與準備教學資源后，教師再引領其經歷一個建模過程，這樣不但利于教師找尋數學知識的生長點，亦能促使學生有準備地建構數學模型。

（責編金鈴）

［中圖分類號］G623.5

［文獻標識碼］A

［文章編號］1007-9068（2016）01-005