混合雙分數布朗運動環境下違約概率的動態研究
張 杰,陳宗新,馬海燕(蚌埠學院 數學與物理系,安徽 蚌埠 233000)
?
混合雙分數布朗運動環境下違約概率的動態研究
張杰,陳宗新,馬海燕
(蚌埠學院數學與物理系,安徽蚌埠233000)
摘要:隨著經濟全球化的發展,企業越來越重視對信用風險的管理.目前,在金融界對信用風險的定價和規避是非常具有實際意義的.在假設企業的總資產價值遵循混合雙分數布朗運動的前提下,本文研究企業的違約概率隨參數值變化的期限結構性態,為企業風險的規避提供決策.
關鍵詞:混合雙分數布朗運動;違約概率;動態分析
目前,隨著經濟全球化程度的增加,企業對信用風險的管理提出了更高的要求.違約概率是客戶信用評級的基礎,是指借款人未能履行合同約定而導致企業損失的可能性.從信用風險的管理系統中,更重要的是研究違約概率對市場化結構模型的參數值的靈敏度.1974年Merton開創了經典的結構化模型,在該模型中假定公司總資產價格滿足幾何布朗運動,但是事實證明幾何布朗運動描述的資產價格的波動只與現在有關,而與過去無關,這與人們的直覺和市場的真實情況不相吻合.因此,近幾年,國內外一些學者通過考慮利用分數布朗運來刻畫標的資產的價格,事實證明分數布朗運動具有長程相依性并能較好地模擬股票的市場價格.但是利用混合雙分數布朗運動研究信用風險的管理的成果并不多,本文首次嘗試建立混合雙分數布朗運動模型對企業的違約概率進行動態分析,為企業預測損失,防范風險提供一定的指導意見.
1 市場結構模型
1.1雙分數布朗運動
指標H∈(0,1)與K∈(0,1]的雙分數布朗運動是指均值為0,協方差函數為


的一種中心高斯過程,雙分數布朗運動記為:BtH,k.
1.2混合雙分數布朗運動的定義
假設σ,ε為兩個常數,且σε≠0.同一個概率空間(Ω,F,P)上一個混合雙分數布朗運動是指雙分數布朗運動BtH,K與一個獨立布朗運動Wt的線性組合稱為,記為:XtH,K
即XtH,K=σBtH,K+εWt
1.3混合雙分數布朗運動模型
假設企業的總資產價值V滿足
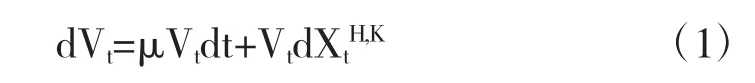
在下文中記標準正態隨機變量的累積分布函數為:
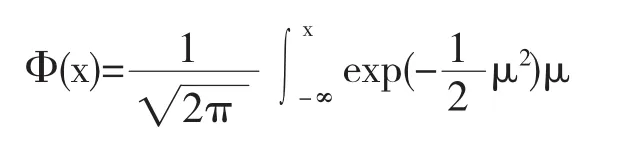
2 違約概率的結構模型及敏感性分析
假設企業的債券價格在τ時為F(V,τ),股權價值在τ時為f(V,τ),τ=T-t.企業違約只發生在到期日企業總資產價值不能償還債券的面值,即Vt f(V,τ)-Vp(V,τ)=V-Be-rτ 式中Vp(V,τ)為歐式看跌期權價格.由引理1可知 其中 于是 因此風險債券的表達式: 上面的(3)式可以表示債券發行人的生存概率,因此在結構模型下的違約概率可以表示為 從Q(lt,τ)的表達式中,可以看Q(lt,τ)是Vt和τ的函數,且Q(lt,τ)介于0與1之間.(5)式還能看成歐式看跌期權Vp(V,τ)近似上界的估計值,因而當V增加時,Q(lt,τ)趨于0,當V減少時,Q(lt,τ)趨于1. 本文首先通過介紹混合雙分數布朗運動,緊接著建立混合雙分數布朗運動結構化市場模型,在此基礎上,對違約概率的敏感性進行分析,為企業防范風險具有一定的幫助作用. 參考文獻: 〔1〕蘇宇,鄧國和.分數次布朗運動模型的信用風險管理[D].廣西師范大學,2009. 〔2〕荊卉婷,龔天杉,牛嫻,等.混合雙分數布朗運動驅動的信用風險模型[J].黑龍江大學自然科學學報,2012,20(2):10-25. 〔3〕Hund J. Default probability dynamics in Structural Models[J]. The Journal of Fixed-Income,2003,9: 67-69. 〔4〕Merton R.C. On pricing of corporate debt: the risk structure of interest rate [J].Journal of Finance,1974,29(2):449-470. 基金項目:2014年國家級大學生創新創業訓練計劃:具有長程記憶性的信用風險模型研究(201411305017) 收稿日期:2015年11月26日 中圖分類號:O211.6 文獻標識碼:A 文章編號:1673-260X(2016)01-0026-02
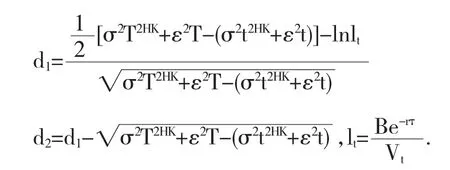

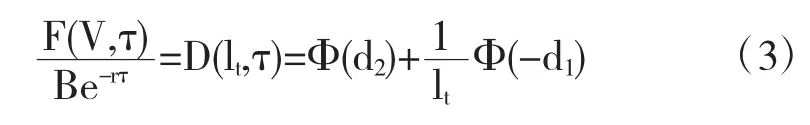
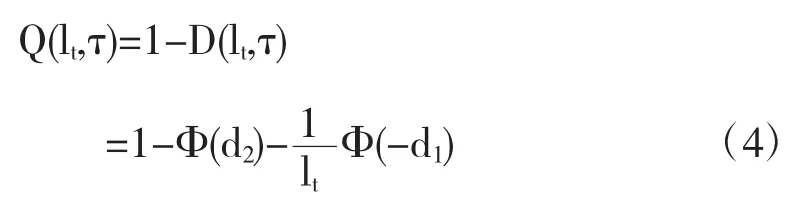
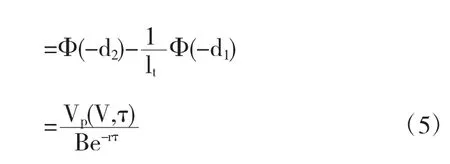
3 結論

