風切變對風電場發電量變化趨勢的影響分析

文 | 楊濟暢，包振海

?

風切變對風電場發電量變化趨勢的影響分析

文 | 楊濟暢，包振海

風能是自然界產生的取之不盡、用之不竭而又不會產生任何污染的可再生能源。近兩個世紀以來，在常規能源告急和環境污染的雙重壓力下，風電因其自身獨有的優點，在很短的時間內便獲得巨大發展。我國風電事業起步較晚，但作為全球風能資源最為豐富的國家之一，我國的風電發展在短短數十年間取得了巨大的成就。2013年我國（除臺灣地區外）新增裝機容量為16088.7MW，累計裝機容量為91.41GW，均處于全球第一位。但是，隨著我國風電事業的逐步發展，全國風電總裝機量的逐步增大，風能可利用區域的逐步減少，未來我國風電在繼續快速發展的同時，已經呈現出如下的不利趨勢：

1.風電建場區域從風能資源較好地區向風資源一般地區轉移。

2.風電建場區域從簡單平坦地形向復雜地形轉移。

3.風電建場區域從人口稀少地區向人口密集地區轉移。

4.風電建場區域從較好氣候環境向較差氣候環境轉移。

這些變化無疑都大大增加了未來風能資源評估及風電場微觀選址工作的難度，因此必須采取更多的技術手段去保證未來風電場在更差的風能資源狀況下能夠達到一定的發電量。目前常用的技術手段有增加葉輪直徑、提升輪轂高度、改進控制策略、優化功率曲線、降低風電機組損耗等等。前些年由于技術本身的限制，風電機組在達到一定高度后很難再次加高，采用混凝土承臺等手段雖然可以使輪轂高度獲得提升，但效果并不明顯且耗資巨大。隨著近年來材料、工藝、運輸等手段的不斷進步，大范圍提升風電機組輪轂高度已經變得可行。目前國內并沒有針對同種風電機組不同高度下發電量及經濟性的詳細測算與分析。本文通過對低風速復雜地形前提下不同的風電場開發案例進行測算，分析在安全風速前提下提升風電機組塔筒高度對于提升風電場發電量，進而提升風電場收益的促進程度，結合風電場經濟效益給出最佳塔筒高度的計算模式。同時，對不同高度下影響發電量提升效果的主要因素進行了分析。

案例基本概況

案例一擬開發風電場場址海拔高程為950m－1130m，場區植被密度較低，地形為丘陵溝壑。風電場擬開發容量為100MW。案例二擬開發風電場場址海拔高程為83m－450m，場區植被密度較高，地形屬南方典型的丘陵地帶，風電場擬開發容量為50MW。

案例一區域內有一座80m高的測風塔，案例二區域內有一座120m高的測風塔，兩個區域內測風數據收集已滿一年以上，數據完整率分別達到92%及94%，滿足風能資源評估要求。風電場基本風能資源狀況統計如表1所示，根據《風電場風能資源評估方法》(GB/T18710-2002)風功率密度等級評判標準，兩個風電場風功率密度等級均不到2級，風能資源較差。

表1　案例基本風能資源狀況統計

選擇符合風電場安全強度等級（IEC III A），適合于低風速條件且性價比較高的多型國內主流風電機組計算發電量。最終案例一與案例二中發電量最大的均為WTG－1型風電機組（輪轂高度85m），其中案例一中選用50臺WTG－1型風電機組，年發電等效小時數為1854h，案例二中選用25 臺WTG－1型風電機組，年發電等效小時數為1925h。

不同塔筒高度經濟性評估

由于案例一及案例二中風電場屬于風能資源較差區域，考慮到兩項目極大風速遠低于風電機組生存極限風速，可以采用提高風電機組塔筒高度的方式，提高項目整體發電量。

以每5m為步長，將WTG－1型風電機組塔筒從85m提升至130m，保持風電機組功率曲線及風能資源數據、風電機組機位不變，分別計算發電量，結果如圖1和圖2所示。

隨著塔筒高度的逐步增加，項目發電量也獲得了明顯的提升。但是隨著塔筒高度的增加，塔筒中電纜采購價、塔筒采購價、風電機組基礎造價、吊裝費用等也在相應增加，而且隨著制造、施工難度的加大，工程投入的增幅也會越來越大。

此處根據工程經驗，給出工程投入各參數的計算公式：

1.電纜：每臺單價=5（米）×400（元/米）×12（根），即塔筒每提升5米，每臺風電機組電纜采購價增加2.4萬元。

2.利息：目前利率按4%計算。

3.吊裝總費用：Xn=Xn-5+[(n-H-5)/5*M+P] （1）

其中Xn為塔筒高度為n時的吊裝總費用，Xn-5為塔筒高度為n-5時的吊裝總費用，n為塔筒高度（n≥90），H為最初塔筒高度，M為風電機組數量，P為吊裝補償系數，根據吊裝廠家報價不同及風電機組數量不同選擇，此次案例一選P=500、案例二選P=270。最初塔筒高度的吊裝費用由工程單位直接給出。

4．風電機組基礎單價：Yn=Yn-5+[（n-H）/5+1]， （2）

其中Yn為塔筒高度為n時的基礎造價，Yn-5為塔筒高度為n-5時的基礎造價，n為塔筒高度（n≥90），H為最初塔筒高。最初塔筒高度的基礎造價由工程單位直接給出。

5.塔筒單價：Zn=[R+0.01（n-H）]n （3）

其中R為塔筒價格系數，R=鋼鐵價格（萬元/t）×最初塔筒質量（t）/最初塔筒高度（m），此次WTG－1風電機組R取1.81萬元/m，Zn為塔筒高度為n時的塔筒單價，H為最初塔筒高度。

根據式（1）、式（2）、式（3），具體收益計算結果如表2所示。

表2　各案例經濟效益評估表（單位：萬元）

實施風電場定制化的目的是，在提高發電量的基礎上實現收益的最大化，而并非是單純的實現發電量的最大化。塔筒高度與收益之間必然存在一個平衡點，在這個點之前，提升塔筒高度可以獲得收益的提升，超過了這個點，提高塔筒高度所獲得的發電量收入難以抵消工程投資的大幅增加，反而會降低收益。

從圖2可以看出，案例一中，120m高度即為整個工程的收益平衡點，當塔筒高度達到120m時，風電場20年總收益在85m高度的基礎上提升了7836.46萬元，達到最大值。塔筒高度超過120m后，風電場20年總收益反而降低。案例二中當塔筒高度達到100m時，風電場20年總收益在85m高度的基礎上提升了903.5萬元，達到平衡值。塔筒高度超過100m后，隨著塔筒高度的增加，風電場20年總收益反而降低，甚至在130m高度會出現負值，即塔筒提升到130m高度時的發電量額外收益無法抵消增加的工程投入，實際收益反而會低于85m高度時的收益。

案例一與案例二之所以平衡點不同，是因為案例一與案例二地形、地址條件的不同，導致吊裝、風電機組的基礎以及發電量均產生差別，最終導致案例二在100m高度時達到了平衡點。

提高塔筒高度與發電量提升的分析

一、風切變對發電量的影響

借助美迪WT軟件，模擬所有風電機組點位處各高度平均風速，并對各高度風速值分別取平均值，統計結果如表3所示。

表3　風電機組點位處各高度風速平均值統計表

隨著高度的提升，空氣密度逐漸變小，且由于高空氣流的逐漸穩定，高度對氣流速度的影響在逐漸變小，導致風速因高度提升所造成的增幅逐漸變小。最終必然導致風電機組發電量增幅也會隨著高度的提升而減少。也就是說，雖然增加塔筒高度可以提升風電機組發電量，但是隨著高度的逐漸增加，這種提升的效果會變得越來越差。如圖4所示，隨著高度的提升，發電等效小時數增幅的走勢曲線呈下降趨勢，正是這種現象的具體表現。

提升同等高度下，案例二的發電量增幅明顯小于案例一，這是因為不同的風切變指數導致提升相同高度下風速的增幅不同。案例一與案例二擬合風切變指數的不同（案例一為0.12，案例二為0.082），導致在提升相同的高度時，案例一的風速增幅明顯大于案例二，相應的，案例一的發電量增幅也大于案例二。

二、大氣熱穩定度對發電量的影響

圖4中的各案例發電小時數增幅雖然在總體上不斷減小，但是在100m、105m及110m高度上呈現出了不同的趨勢（圖4中紅圈所示），案例一整體呈下降趨勢，案例二則有降低－升高－降低的波動。

相應的，案例二中每5m高度風速差值在100m至95m、105m至100m、100m至105m三個高度區間同樣出現了波動（圖5中藍圈所示），并非如案例一一樣呈現整體下降的趨勢。

目前，美迪 WT軟件可以借助兩個不同高度的溫度，結合流場模擬結果，針對風電場進行熱穩定度等級分布計算。此次案例二中所用測風塔在8m、80m及120m高度各安裝有一個溫度傳感器，將實測數據導入軟件進行模擬，其計算結果與未進行熱穩定度校正的案例一產生了明顯的不同。圖6是國外某風電場實測風廓線與軟件模擬風廓線的對比。虛線是在不考慮大氣熱穩定度的情況下，通過軟件計算得到的風廓線，而實線則是在同等情況下，通過實際測量獲得的風廓線。

圖6中兩種結果差異巨大，因此，單一的將大氣熱穩定度設置為中性（即不進行校正）進行風能資源分析與評估是不合理的，計算得出的結果也必然會與實際情況產生極大的誤差。目前國內幾乎所有測風塔均只設置一個溫度傳感器，在測風階段就已經喪失了后續進行大氣熱穩定度校正的機會。這種現象必須得到遏制，未來在制定測風方案時，必須對測風塔高度及傳感器數量和種類進行更加精確的配置，以保證測風數據能夠更好的代表該區域實際風能資源狀況。

三、發電等效小時數計算公式

給出塔筒高度與發電等效小時數的近似計算公式：

式（4）中，p、V0分別為風電場50m高度處的平均空氣密度與風速，H為所求塔筒高度，α為測風塔處擬合風切變指數，H0為風電機組初始輪轂高度，T0為風電機組初始輪轂高度處的發電等效小時數，p0為標準空氣密度(1.225kg/m3)，L為校正系數，L取值范圍如表4所示。

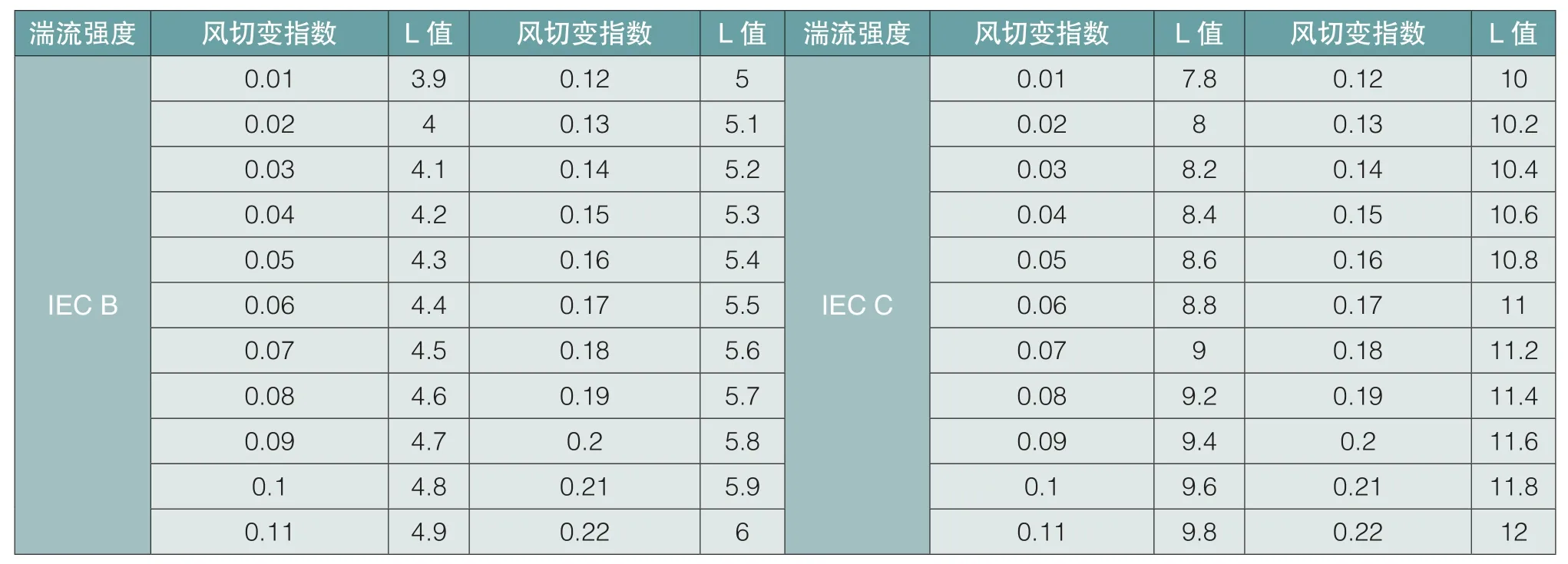
表4　L取值一覽表

從圖7可以看出，公式計算結果會略大于軟件實際計算結果，但最大誤差不超過0.5%。對此次軟件計算的發電成果進行統計，根據統計結果，以原有塔筒為基準，在一定提升范圍（45m）內，風切變指數為0.12時，塔筒高度每提升5m，發電量平均可提升1.22%左右；風切變指數為0.082時，塔筒高度每提升5m，發電量平均可提升0.84%左右。目前國內研究結果表明，當風切變指數為0.2時，塔筒每提高5m，發電量可提升1.5%左右。故在公式（4）中，將風切變指數調整為0.1和0.2，其他參數不變，分別對案例一與案例二進行計算，結果統計如表5所示。

根據計算結果，當風切變指數為0.1時，相對于85m高度的發電量，平均每提高5m高度，案例一與案例二分別可提升發電量1.14%和0.91%左右。當風切變指數為0.2時，案例一與案例二分別可提升1.64%和1.29%左右。造成案例一、案例二在相同風切變下提升效果不同的主要因素是湍流的影響，如果此處對案例一與案例二取平均值，則在風切變指數為0.1及0.2時，平均每提高5m高度，發電量分別可提升1.025%和1.465%。這與式（1）中研究結果基本吻合。

以上結果初步證明公式（4）計算結果具有較高的可信度，因此在技術條件不具備的情況下，可以利用公式進行粗略的推算與分析，在確定提高風電機組塔筒高度對于風電場具有較好經濟性的情況下，再進行詳細的論證。

結論

在低風速、復雜地形條件下，以保證風電機組安全為前提，提高風電機組塔筒高度對于提升風電場發電量，增加風電場收益具有積極的作用。隨著高度的提升，高度對氣流速度的影響在逐漸變小，導致風速因高度提升所造成的增幅逐漸變小，最終必然導致風電機組發電量增幅也會隨著高度的提升而減少。而在不同的風電場，由于風切變指數的不同，導致同種風電機組提升相同高度所增加的發電量也不相同，一般情況下，風切變指數越大，發電量提升越大。由于塔筒高度的提升造成制造、施工的難度在迅速上升。因此，發電量收益增幅的降低和工程投入增幅的變大，必然使風電機組塔筒高度存在一個可計算的平衡值，在這個平衡值上風電場將實現發電量收益的最大化。

大氣熱穩定度對于風電機組發電量有著很大的影響，如果不對大氣熱穩定度進行計算，可能會造成風電場實際發電量遠低于設計發電量的嚴重后果。目前，利用兩個高度的溫度可以進行大氣熱穩定度的校正，前提是測風塔設備及高度必須進行合理配置。

在不進行軟件計算的情況下，不同塔筒高度下的發電等效小時數可由公式近似計算，兩個案例的計算結果顯示，公式計算結果與軟件計算結果誤差不超過0.5%。在決定是否對一個風電場項目采取加高塔筒的設計措施時，必須進行詳細的發電量與經濟性評估，權衡利弊，最終實現風電場定制化設計的最終目標：風險最小化、收益最大化。

（作者單位：特變電工新疆新能源股份有限公司）