基于蟻群優化的多目標社區檢測算法

楊楠呂紅娟++陳婷

摘要：蟻群優化算法作為單目標優化問題，由于只有一個目標函數，通常會將解限制到特定的范圍內。當優化的目標不恰當時，算法可能失效，比如分辨率限制問題。我們將多目標優化的思想與傳統的用于社區檢測的蟻群優化算法相結合，增加了目標函數個數，即增加了解的評價指標數目。該算法引入多目標策略，提出多目標ACO算法，該算法在一次運行過程中會產生一組Pareto最優解。并在三個真實世界網絡證明該算法的有效性和準確性。

關鍵詞：復雜網絡；社區檢測；蟻群優化算法；多目標優化

中圖分類號：TP18文獻標識碼：A

1引言

1991年意大利學者Dorigo M等人首次提出了蟻群優化算法[1，2]引起了學者的廣泛關注與研究。蟻群算法是一種基于種群的啟發式仿生進化系統，該算法采用了正反饋分布式并行計算機制，易于與其它方法相結合并且具有較強的魯棒性。

本文介紹了一種基于蟻群優化的多目標社區檢測方法，將蟻群優化算法與多目標策略[3]相結合，是一種優化模塊度的社區檢測方法。對于多目標優化問題，通常無法得到最優解，若同時考慮多個目標函數則算法將會得到一組優于其它解的最優解集。該集合叫做帕雷托（Pareto）解集或者非支配解集。

2基于蟻群優化的多目標社區檢測

蟻群優化算法（ACO），是一種基于螞蟻覓食行為的啟發式方法，用來解決困難的組合優化問題，并且已經成功的應用到了各種棘手的問題，像二次分配問題（QAP），車輛路徑問題（VRP）等。在1996年，Gambardella等人提出了一種修正的蟻群優化算法——蟻群系統（Ant System，AS），已經成功地應用在旅行商問題上。在這之后，科學家們也發明了一些改進的算法，比如精英蟻群系統（Elitist Ant System，EAS），最大最小蟻群系統（MaxMin Ant System，MMAS）以及排序蟻群系統（RankBased Ant System，ASrank）。

運用蟻群優化來做社區檢測，首先需要指出如何表達一個解，其次就是如何構建一個解，然后就是信息素的初始化以及更新。下面我們將詳細描述該算法。

2.1編碼方式

社區就是復雜網絡的子圖，因而檢測社區結構就等價于找出能揭示網絡最好分割的一組子圖。因此，社區檢測問題的解可以明確地表示為：一個n個元素的向量表示圖，其連通分量相當于社區。向量的元素和索引對應于圖G=（V，A）中的節點。例如，向量中第i個元素等于j，即節點Vi和Vj之間有邊相連，也就是說這兩個節點在同一個連通分量里面，即處于同一個社區。

該編碼框架的優點有很多，最重要的是不需要預先知道復雜網絡的社區劃分數目。解碼的過程需要找出所有的連通分量。所有屬于同一個連通分量的節點被劃分到一個社區，解碼過程是有必要的且可以通過廣度優先搜索（breadthfirst search，BFS）或者深度優先搜索（depthfirst search，DFS）在線性時間內完成。解碼完成后，會得到一個表示每個節點歸屬的向量。這種基于基因近鄰的編碼框架已經應用到了多目標聚類領域。該框架在社區檢測的應用中有幾個主要的優點，最重要的是，不需要預先知道社區的真實劃分數目K，因為在解碼過程中能夠自動地得到K的取值。

3.1真實世界網絡

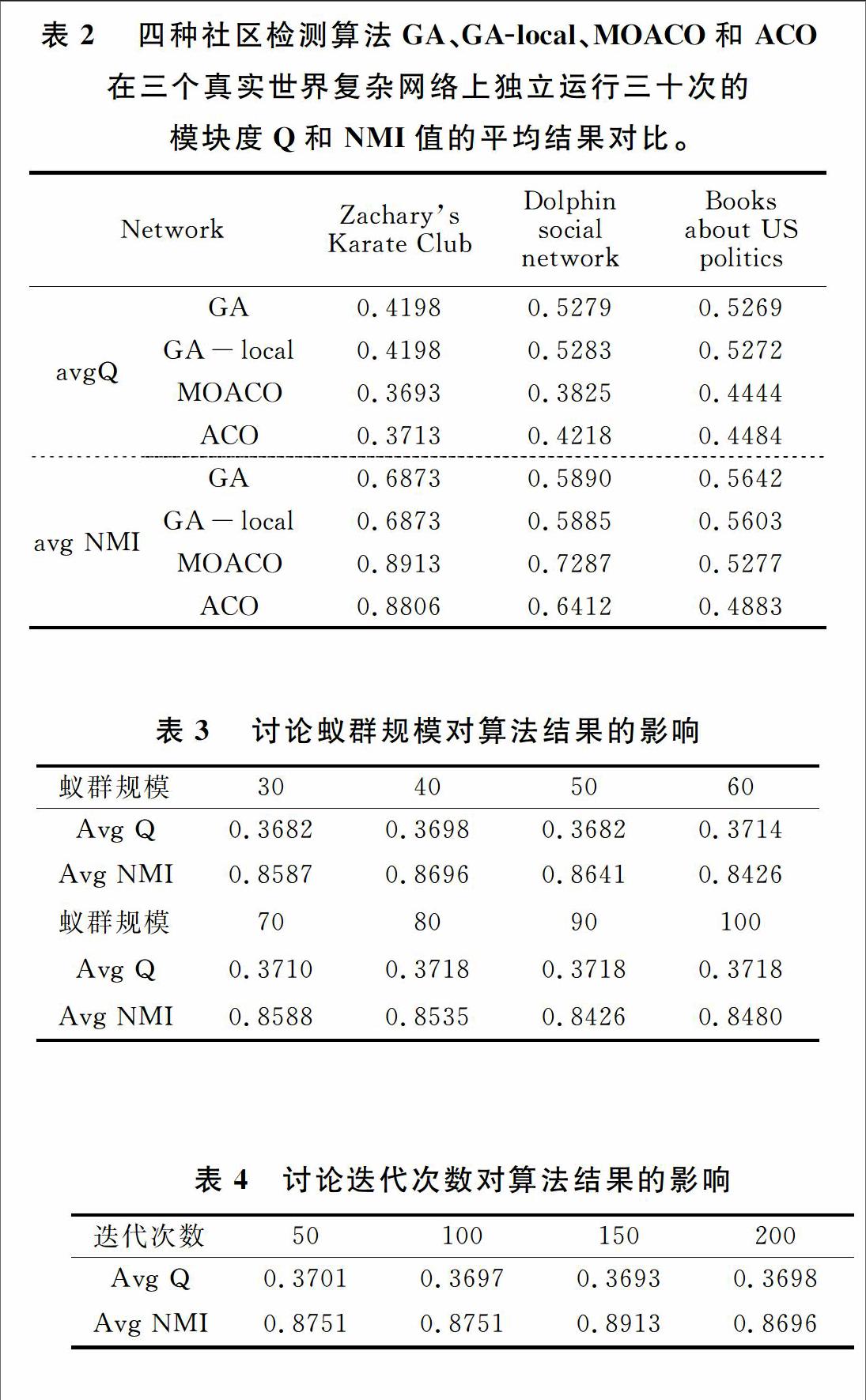
本節將MOACO算法應用在三個真實世界網絡上，分別是Zacharys Karate Club、Bottlenose Dolphins、Books about US politics。以上復雜網絡是社會網絡分析領域中的經典數據集，將這些數據在并與沒有加入多目標策略的ACO算法以及GA、GAloacal算法進行了對比。由表2可以看出，三十次獨立運行后，在Zacharys Karate Club網絡中，ACO和MOACO的平均模塊度值均不如GA和GA-local算法的結果好，而MOACO和ACO的平均模塊度相差不大；在Dolphin social network網絡中，本文提出的MOACO算法的平均NMI值明顯好于其它算法。在Dolphin social network網絡中，MOACO算法的模塊度Q平均值與ACO算法的結果相差不大，而NMI的平均值要好于ACO算法。

為了驗證蟻群規模和迭代次數對算法的影響，以Zacharys Karate Club網絡為例進行參數分析，參數α、β、T、ρ、ε的值不變化，算法獨立運行三十次求平均模塊度值Q和平均NMI值，討論蟻群規模N對算法結果的影響。

由表3可以看出，隨著蟻群規模的增加，平均模塊度值呈增長趨勢，在蟻群規模為80時，達到了最大值。而由于蟻群優化算法中螞蟻個體選擇路徑是隨機的，因而平均NMI值沒有呈現一定的規律，而當蟻群規模為40時，平均NMI值取得最大值。

表4表示參數α、β、N、ρ、ε保持不變，討論迭代次數T對算法結果的影響，算法獨立運行三十次的算法結果如表4所示。

由表4可知，迭代次數對算法的平均模塊度值影響不大，而當迭代次數為150次的時候，平均NMI值取得了最大值。

圖2表示調節參數過程中，算法取得的最優結果，即每一次運行的模塊度值和NMI值，data1表示平均模塊度值，data2表示平均NMI值。最優參數為：迭代次數150次，種群規模40。可以看出模塊度值非常穩定。

3.2計算機仿真網絡

本節使用經典的GN benchmark復雜網絡來檢測算法的可行性和有效性。GN基準網絡是由Newman等提出。對于該基準網絡，每個圖包含了128個節點，分為4個由32個節點構成的社區。每個節點平均有Zin條邊與同社區內節點連接，Zout條邊與社區外節點連接。其中Zin+Zout = 16，作為每個節點的期望的度。隨著Zout的增大，所產生的隨機網絡給社區檢測算法帶來了更大的挑戰。特別是當Zout大于8時，意味著每個節點在社區內的邊都要小于社區外的邊，這時網絡的社區結構就會非常模糊。當Zout≤ 8時，節點外度所占的比例小于內度所占的比例，因此算法應該能檢測出網絡中存在的社區結構，當Zout = 0時，表明節點的外度為0，此時節點僅與自身社區內的節點相連接，社區結構非常明顯。分別對Zout從0到2進行了測試，對每種類型的網絡產生一個復雜網絡，使用NMI來衡量算法檢測的結果和真實網絡劃分之間的相似性。對于每個網絡，計算三十次獨立運行的平均值。

由表5可以看出，當GN網絡的外度為0時，該算法可以準確地檢測出網絡劃分情況；當GN網絡的外度為1和2的時候，該算法得到的結果也還都是有效的。

但是，在蟻群優化方法中，其算法復雜度比較高，所需要的搜索時間很長，而且容易出現所有的螞蟻所對應的解完全相同這種“停滯現象”。導致了當復雜網絡的社區數目較大時，算法不能產生有效解。另外，該算法對計算機生成的仿真網絡不能得到有效的結果，這是我們進一步研究的內容。

4小結

基于傳統的蟻群優化算法（ACO）算法的缺陷，提出了一種用于復雜網絡社區檢測的多目標蟻群優化算法MOACO，該算法將繼續沿用傳統的基于模塊度優化的策略，加入了多目標的思想，每次迭代過程中，根據兩個目標函數的不同折中，最終得到Pareto解集，選取每一代中優先級最高的那一組解。在三個真實世界網絡和GN網絡中的外度較小的網絡上證明了算法的有效性，并將提出算法與ACO算法進行了比較，NMI平均值要優于ACO算法，模塊度Q的平均值與ACO算法相當。缺點是不能處理社區劃分類別多的復雜網絡，對于結構模糊的GN網絡，算法的效果不明顯。

參考文獻

[1]HONGHAO C， ZUREN F， ZHIGANG R. Community detection using ant colony optimization [C] Evolutionary Computation （CEC）， 2013 IEEE Congress on. IEEE， 2013： 3072-3078.

[2]DORIGO M，BIRATTARI M，STUTZLE T. Ant colony optimization[J]. Computational Intelligence Magazine， IEEE， 2006， 1（4）： 28-39.

[3]SOLNON C， Ghédira K. Ant colony optimization for multi-objective optimization problems[J]. Internation Journal on computer science， 2010.

[4]GONG M， CAI Q，CHEN X， et al. Complex network clustering by multiobjective discrete particle swarm optimization based on decomposition[J]. Evolutionary Computation， IEEE Transactions on， 2014， 18（1）： 82-97.

[5]SRINIVAS N，DEB K. Muiltiobjective optimization using nondominated sorting in genetic algorithms[J]. Evolutionary computation， 1994， 2（3）： 221-248.