2015年高考數學山東卷文理比較研究

劉胡良

【摘 要】 在我國現行的高考制度中，實行文理分科考試，數學作為一門文理必修的基礎學科，文理科數學存在著一定的差異，因此歷年高考中對于文理科數學的差異化處理也是一個備受關注的問題。在本文中，筆者以2015年高考數學山東卷為例，從文理科學生比較、試卷結構、難度控制等方面入手進行了比較研究，希望能夠為高考命題、中學教學等提供參考.

【關鍵詞】 高考數學；文理分科；試卷分析

1 引言

自1977年我國恢復高考制度以來，為分類選拔人才，高中實施了文理分科[1].數學作為一門文理必修的基礎學科，文理科數學在內容范圍、能力要求等方面都存在著顯著的差異，教學中的差異必然導致在高考數學試卷中的文理差異，具體體現在有一些試題是相同的，同時存在著許多在知識與能力要求方面不盡相同的試題.高考數學中文理差異的處理也是備受關注的問題，歷年高考數學山東卷都希望恰當地處理文理的差異，筆者結合2015年高考數學山東卷分析高考數學的文理差異處理，希望為高考命題、教師教學以及學生學習提供參考與建議.

2 文理科學生比較

學生是教學的主體、學習的主人，要恰當處理文理差異首先必須了解學生.

文理科學生在思維特征、學習方法、情感態度、個體差異等方面都存在著較大的區別.在思維特征方面，文科學生更加擅長形象思維，理科學生往往更加擅長抽象思維、邏輯思維.而數學是一門思維的科學，思維方式的差異導致文理科學生在學習方法上也不盡相同，文科學生經常采用形象思維的方式來學習數學，課堂上忙于機械抄錄，注重記憶，而忽視思考和自主演算的過程，理科學生則經常會更加關注知識的邏輯推理、自主演算.在情感態度方面，許多文科學生對數學不感興趣，甚至抱有一種恐懼的心理，相比較而言，這類學生在理科學生中所占比例較低.在個體差異上，根據歷年高考考生在數學科的答題數據可以看出，文科考生的數學水平分布離散化程度高，方差大，即文科考生之間的水平差異非常明顯，而理科考生數據接近于正態分布.

3 試卷結構

試卷結構分為顯性結構與隱性結構，前者是試卷的框架結構和題型結構，后者是試卷的知識結構、能力結構以及難度結構[2].我們將重點從知識結構、能力結構入手分析2015年高考數學山東卷對于文理差異的處理.

3.1 知識結構

知識結構是試卷內在結構中最基礎、最重要的結構，其中包括：試卷所考查的知識內容是什么？占規定考試范圍的百分比如何？各項知識所占比例如何？

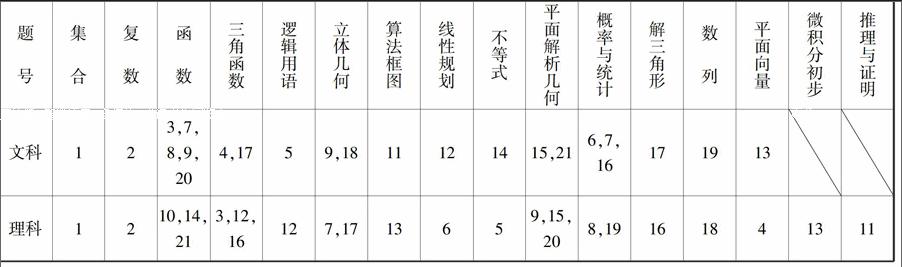
我們統計了2015年高考數學山東卷的知識結構表如下：

由上表可以看出，2015年的高考數學山東卷在全面考查知識點的基礎上，對重點內容進行了重點考查.文科試卷考查了《考試說明》中所要求的20個知識模塊中的17個，理科試卷考查了所要求的全部22個模塊.函數是高中數學的核心內容，而且是繼續學習高等數學的基礎，所以函數（包括三角函數）相關性質的考查在歷年高考中都占據了極其重要的地位，2015年的高考中，文理科這部分內容的占比都達到了總分值的1[]3左右，大約占50分.高中數學的另一塊核心內容是幾何，包括了平面解析幾何、立體幾何，文理科對這部分內容的考查都在40分左右，同樣占據了非常重要的位置.其他的重要知識點，包括概率統計、數列等，也都進行了充分的考查.這種重點考查，兼顧全面的考查方式符合高中數學學科特點，有利于引導高中教學.3.2 能力結構

近年來高考命題更加注重對考生能力和素質的考查，“能力立意”逐漸成為命題的指導思想和基本原則.“能力立意”在學科中的具體體現就是注重考查相應的學科能力，學科能力是學生的智力、能力與特定學科的有機結合，是學生的智力能力在特定學科中的具體體現.數學學科將能力分為7大部分，分別為運算求解能力，數據處理能力，空間想象能力，抽象概括能力，推理論證能力，應用意識和創新意識[3].

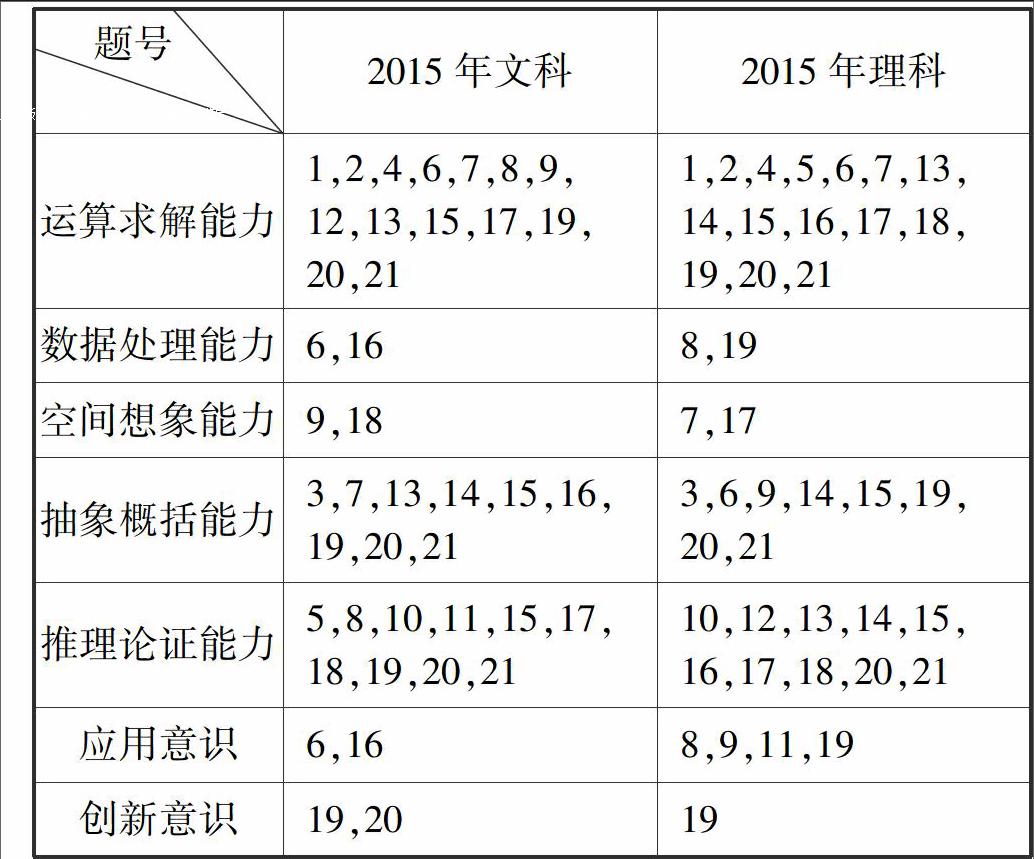
2015年高考數學山東卷能力考查統計如下表：

由上表可以看出，2015年高考文理試卷都實現了數學七大能力的全覆蓋，但各種能力所占比重不盡相同，運算求解能力、抽象概括能力、推理論證能力在文理科中都占據了突出的地位，這樣的處理方式是由數學的學科特點決定的：數學是思維的學科，數學思維的培養是數學教育的核心要求之一，而抽象概括能力和推理論證能力是數學思維的重要表現與立足點，因此高考數學試卷必然對抽象概括能力和推理論證能力進行重點考查.同時，運算求解能力的考查幾乎在每道題目中都有所體現，當前在數學教育界有一種呼聲，希望大幅度降低高考試卷中運算量的考查，筆者認為對于這樣的呼聲應該理性看待，降低運算量并不等于降低對運算求解能力的要求，而是要減少繁瑣的、重復的程序化演算，恰恰是突出了能力的地位.恩格斯認為“數學是一門研究數量關系和空間形式的科學”，數量關系必然離不開運算求解，而且隨著近代數學的發展，數量關系的地位愈發突出，甚至空間形式的研究也需要借助數量的精確化，因此運算求解能力的基礎性作用也更加突出，運算求解能力的要求不應降低，高考命題應注重研究如何減少繁瑣、機械的運算量考查而加強運算求解能力的考查，同時在教學過程中如何避免題海戰術同時增強學生的運算求解能力也是一個值得思考的問題.4 難度控制

試卷的難度是對考試要求的集中反映，對難度的有效調控是實現考查要求的有效手段，其中試題的難度是試卷難度的具體體現，代表了試題對考生知識和能力的適合水平及要求[1].高考作為高利害性考試，考試難度是備受社會關注的焦點，針對文理差異，合理調控難度是值得深入研究的問題.2015年高考數學山東卷主要從以下幾個方面入手調控試題難度，處理文理差異.

4.1 試題的綜合性

新的《課程標準》與舊大綱相比，更加明確地強調了對相關知識綜合運用的要求，所以高考試題更加注重在知識網絡的交匯點處設計試題，使對數學基礎知識的考查達到必要的廣度與深度.在一道試題中，交匯的知識點越多，綜合性就越強，試題的難度也就越大.理科試題往往比文科試題具有更強的綜合性.

4.3 對能力不同層次的要求

現在的高考命題更加注重對能力和素質的考查，以能力立意為指導思想，注重以知識為載體，從問題入手，把握數學學科整體意義，考查考生對知識的理解和應用，尤其是在不同情境中的綜合、靈活運用能力，從而檢測考生理性思維的廣度和深度以及進一步學習的潛能.文理科學生自身的差異、學科培養目標的差異決定了高考數學中對于考生能力要求的不同，相比較，理科的能力層次要求更高，更加注重對于知識的綜合、靈活運用.例5 （2015年高考山東卷文科第21題）

兩個題目描述的是同一個橢圓，但描述的方式卻差別較大，例5給出的是純代數的描述方式，考生只需將橢圓上的點（3，12）代入方程，同時根據e=ca=32，即可解出相應的a，b，c的值，考查的是基礎的運算求解能力.而例6同樣求橢圓方程，題干給出的卻是代數與幾何結合的描述方式，需要考生從幾何關系中發現隱藏的代數關系2a=4，這樣的處理方式對于考生的抽象概括能力、數形結合能力、知識遷移靈活運用的能力都提出了更高的要求.

5 結語

高考文理分科考試已實行30多年，十八屆三中全會提出了深化教育招生考試制度改革，高考文理不分科成為了改革的方向，高考文理科試卷也即將成為歷史，但這并不意味著高考數學文理差異的研究已經沒有意義，近期也有多篇文獻（如[5]，[6]）對此做了研究，文理科的巨大差異確實是存在的，一旦忽視這樣的差異，必將給我們的教育改革帶來許多的問題.歷年高考數學試卷文理科差異處理的研究、考試數據的研究對于新一輪的數學文理不分科改革仍然是一筆寶貴的財富，可以為改革的順利進行提供更多的參考.

參考文獻

[1] 陳昂，任子朝.數學文理科試卷難度調控策略[J].數學通報，2011，50（9）：5-8.

[2] 馬云鵬，孔凡哲，張春莉.數學教育測量與評價[M].北京：北京師范大學出版社，2009.

[3] 山東省教育招生考試院.2015年普通高等學校招生全國統一考試山東卷考試說明[M].濟南：山東人民出版社，2015.

[4] 中華人民共和國教育部.普通高中數學課程標準（實驗）[M].北京：人民教育出版社，2003.

[5] 任子朝，陳昂.高考文理不分科后數學科考試內容改革研究—數學科考試內容改革問卷調查分析[J].數學通報，2015，54（6）：1-4.

[6] 任子朝等.高中文理科學生數學水平比較研究[J].課程·教材·教法，2015，35（6）：62-67.