動車運用所調車作業計劃編制優化
郭小樂,宋 瑞,黎浩東,陳勝波,劉星材
(北京交通大學 交通運輸學院,北京 100044)
動車運用所調車作業計劃決定了動車運用所內動車組各項檢修作業的起始、終止時刻以及占用的作業線。合理的動車運用所調車作業計劃可以避免或減少動車組因等待而造成的延誤,從而盡量避免動車組因不能及時完成維修作業而對動車組運用計劃造成影響。
部分學者對于該問題及相關問題進行了研究。文獻[1]以股道聯通關系、股道時空占用相容性等為約束,以減少關鍵線區占用時間和調車路徑費用為優化目標建立優化模型,運用最大最小蟻群算法進行求解。文獻[2]針對動車運用所存車線運用方案進行了研究,以給定動車組占用存車線時間為前提,以提高存車線利用率和減少調車作業走行距離為優化目標,以列位占用相容性條件為約束建立優化模型,運用模擬退火算法求解模型。文獻[3—6]研究了車站股道的運用問題,多以資源的時空占用相容性為約束,以列車對股道的占用情況為決策變量,采用啟發式算法對模型進行求解。文獻[7—12]研究了車間作業調度(Job Shop Scheduling)問題,均采用智能算法進行求解。目前針對動車運用所調車作業計劃編制問題,在各項作業的執行順序不確定的情況下綜合考慮各類作業線運用方法的研究還比較少,實際工作中的調車作業計劃多為人工編制,如果動車運用所內的動車組數量較多,人工編制調車作業計劃的方法將難以滿足作業要求。
本文針對動車運用所調車作業計劃編制問題,以作業線數目、動車組數目以及動車組執行各項作業的順序和占用作業線的時間為約束條件,以動車運用所內動車組總延誤時間最小為目標函數,建立動車運用所調車作業計劃編制優化模型,設計求解該模型的微進化算法及啟發式規則;并用算例驗證模型和算法的有效性和正確性。
1 動車運用所調車作業計劃編制問題描述
解決動車運用所調車作業計劃編制問題就是如何在動車運用所各類作業線數量一定的情況下,合理安排動車組的各項檢修作業,優化作業流程。
動車運用所調車作業計劃編制問題與工廠車間的作業調度問題相似。可以將等待作業的動車組看作等待進行加工的工件,將作業看作機器。但是與車間調度問題不同的是,動車組執行作業的次序是不確定的,在各種類型作業線上停留的時間也是不確定的,并且動車組為完成某項作業必須始終處于某類作業線上,而車間調度問題中的工件則不必始終處于某臺機器上。
以盡頭式布局的動車運用所的一級修調車作業計劃編制問題為例,一級修包括檢修、清洗、轉線、存車4項作業,該種情形下動車組完成各項作業的順序不定,其中檢修和清洗2項作業是必須執行的,轉線作業可與其他3項作業中的任一項合并,存車作業只有在以下4種情況下需要執行。
(1)動車組到達動車運用所時檢修線、清洗線全部被占用;
(2)動車組完成檢修作業而要進行清洗作業時,清洗線全部被占用;
(3)動車組完成清洗作業而要進行檢修作業時,檢修線全部被占用;
(4)動車組完成檢修、清洗作業的時刻早于規定的離開動車運用所的時刻。
所以動車組在存車線上的停留時間并不確定。而且當動車組完成檢修作業或清洗作業但無法轉線時(如尚未執行作業的作業線全部被占用),動車組必須在當前作業線上等待轉線,所以動車組在檢修線和清洗線上的停留時間也不確定。
2 動車運用所調車作業計劃編制優化模型
以動車運用所的一級修調車作業計劃編制問題為例,構建動車運用所調車作業計劃編制優化模型。

對于動車運用所調車作業計劃的編制問題,需要決策的變量如下。
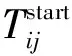

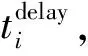

根據上述分析,以最小化動車運用所內所有動車組的總延誤時間T為目標函數,構建如下動車運用所內調車作業計劃編制優化模型。
(1)
s.t.
i=1,2,…,n;j=1,2,…,m;f∈Fj
(2)
i=1,2,…,n;j=1,2,…,m
(3)
i=1,2,…,n;j=1,2,…,m
(4)
i,k=1,2,…,n;j=1,2,…,m;f∈Fj
(5)
i=1,2,…n;j,l=1,2,…,m
(6)
j=1,2,…,m
(7)
(8)
i=1,2,…,n;j=1,2,…,m
(9)
i=1,2,…,n;l=1,2,…,m
(10)
i=1,2,…,n;j=1,2,…,m
(11)
i,k=1,2,…,n;j,l=1,2,…,m
(12)
模型中的約束條件:式(2)為作業線f上的動車組維修順序約束;式(3)為動車組Di執行各項作業的順序約束;式(4)為動車組Di完成作業Yj的開始、結束時刻關系約束;式(5)為不同動車組在作業線f上的作業時間關系約束,即如果動車組Dk緊隨動車組Di在作業線f上作業,則動車組Dk執行作業Yj的開始時刻不早于動車組Di執行作業Yj的結束時刻;式(6)為動車組Di執行不同作業的作業時間關系約束,即對于動車組Di,如果作業Yl緊跟在作業Yj之后,則動車組Di執行作業Yl的開始時刻不早于動車組Di執行作業Yj的結束時刻;式(7)為作業線數量約束;式(8)為動車組數量約束;式(9)為最晚完工時刻約束;式(10)為各非虛擬動車組執行各非虛擬作業所用時間約束;式(11)為作業最早開始時刻約束。
3 模型求解算法
通過以上對動車運用所調車作業計劃編制問題的分析可知,編制1個完整的動車運用所調車作業計劃需要解決以下2個問題。
(1)確定每列動車組執行每項作業的起、止時刻。
(2)確定每列動車組執行每項作業需要占用的作業線。
因此對應地將模型分2個階段求解:第1階段,采用微進化算法求解每列動車組執行每項作業的起、止時刻,進而通過計算該列動車組執行最后一項作業的結束時刻與動車運用所運用計劃規定的出所時刻之差求得該列動車組的延誤時間,最終求得全部動車組的總延誤時間;第2階段,采用啟發式規則求解每列動車組執行各項作業所占用的作業線。
微進化算法是一種新型智能優化算法,它模擬的是生物種群中的個體向種群中的優秀個體學習的過程,并且該算法涉及的參數較少,便于實現,可以有效求解各動車組執行各項作業的起止時刻。已經有學者將微進化算法應用于函數優化問題[13]和實際工程問題[14],取得了良好效果。
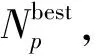
(13)
式中:θ是一個服從期望為0、標準差為δ的正態分布的隨機數。

3.1 個體編碼方式
需要說明以下幾點。
(1)由于列車從到達動車所到離開動車所始終處于3項作業中某一項作業的作業線上,所以下一項作業的作業開始時刻與上一項作業的作業結束時刻相同。
(2)3項作業的開始時刻中必須有1項作業的開始時刻與列車到達動車所的時刻相同。
(3)所有作業的結束時刻必須不早于動車組運用計劃規定的最晚完工時刻。
(4)檢修作業和清洗作業的作業時間均不能小于其標準作業時間。
3.2 作業起、止時刻方案的可行性判斷
由于圖1所示的編碼方式無法保證調車計劃中某一時刻每條作業線上至多停放1列動車組,即不能確保調車作業計劃是可行的,因此引入“時段”的概念。“時段”為某開始時刻和某結束時刻之間的一段時間。對于某項作業,如果有2列動車組執行該項作業的時段存在重疊部分,則說明在該重疊部分表示的時段內這2列動車組在同時執行該項作業,如圖2所示。

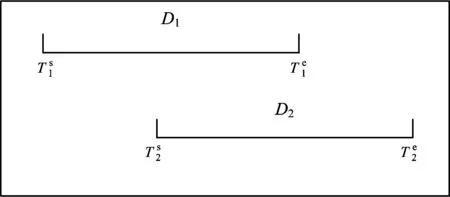
圖2 時段
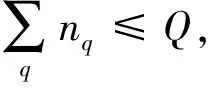
Step 1:初始化。定義變量K=0。令動車組索引i=1。
Step 2:對于動車組Di,定義時段ti=[Ts,Te],Ts和Te分別為動車組Di執行該項作業的開始與結束時刻。
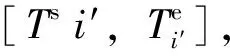
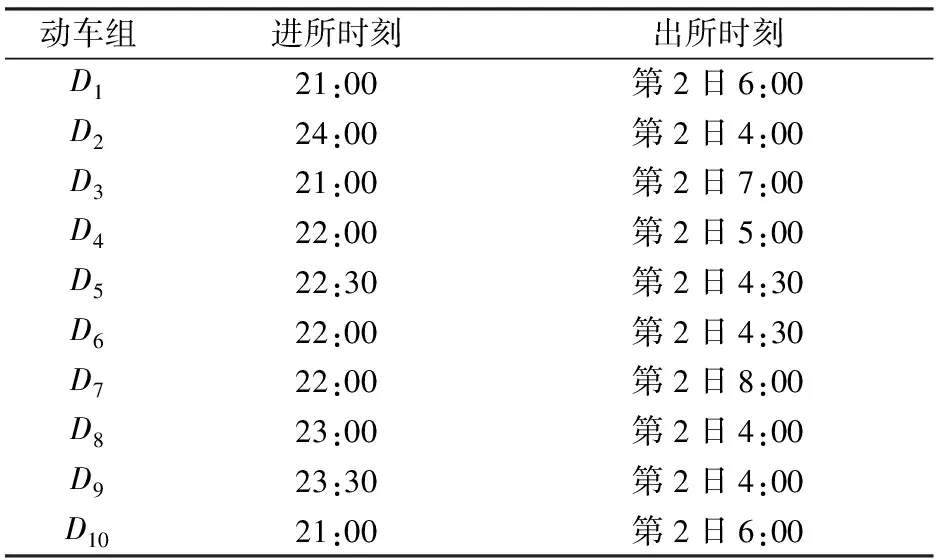
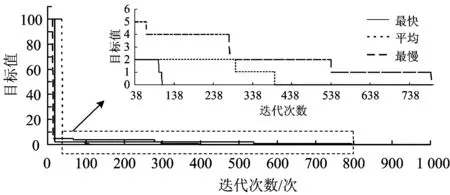
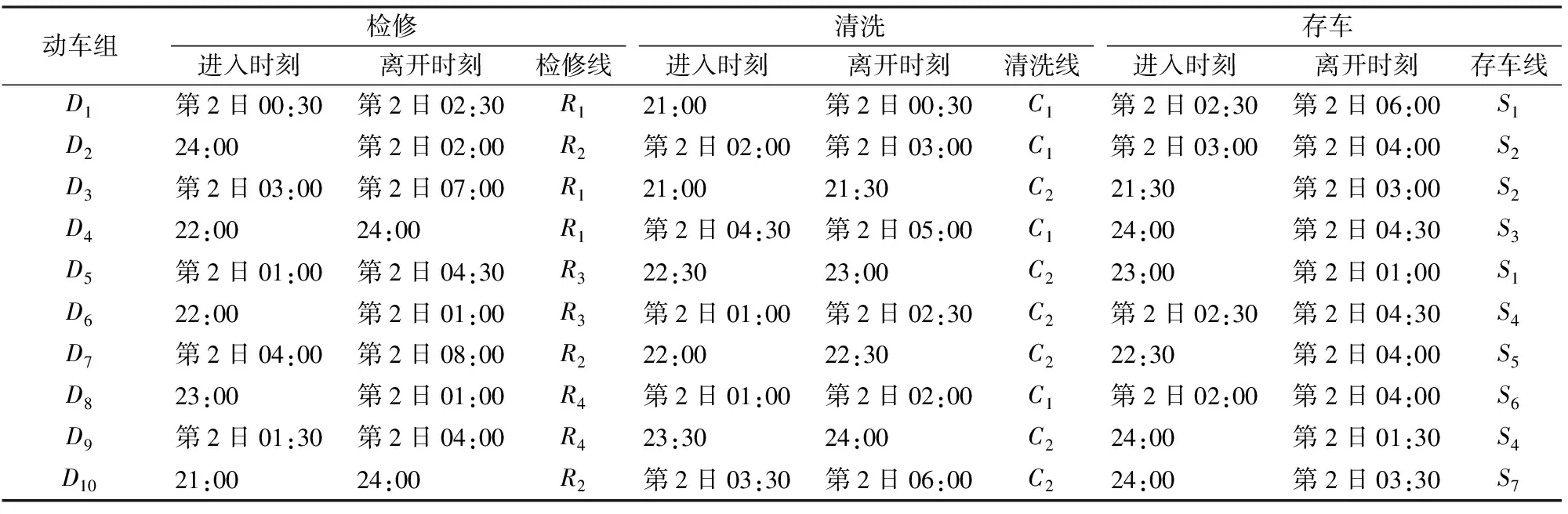
Step 4:如果i′ 按照上述規則分別檢查檢修、清洗和存車3項作業中是否存在重疊的時段,若對于每項作業,同時執行該作業的動車組數均不超過作業線數目Q,則該作業起止時刻方案是可行的,進而通過計算該列動車組執行最后一項作業的結束時刻與動車運用所運用計劃規定的出所時刻之差得到該列動車組的延誤時間,最終求得全部動車組的總延誤時間。計算過程中,允許不可行解的存在。對于不可行解,給予其一定的懲罰值。 采用式(14)更新個體狀態: (14) 個體狀態更新后,如果3項作業中沒有任何1項作業的開始時刻與動車組的到達時刻相同,則隨機選擇1項作業,令其開始時刻與動車組的到達時刻相同。 作業起止時刻方案和總延誤時間計算步驟如下。 Step 1:初始化。令g=0,確定種群規模Z和最大迭代次數,初始化種群,得到每列動車組的作業順序及各作業起止時刻的初始方案。 Step 3:種群進化。對于第g代種群,按照式(14)更新種群中每個個體的狀態,產生第g+1代種群。需要說明的是,更新狀態后,個體中各動車組3項作業的開始時刻必須有1項作業的開始時刻與列車到達動車所的時刻相同。 作業線分配算法實際上是一組規則,按照這組規則,可以在保證無多列動車組同時占用某條作業線的前提下確定每列動車組執行各項作業所占用的作業線。具體算法步驟如下。 Step 1:初始化。對于某項作業,如果屬于該項作業的作業線數目為Q,則定義Q個集合L1,L2,…,LQ。令i=0,j=1。 Step 2:令i=i+1。轉Step 5。 Step 3:令j=j+1。 Step 4:對于動車組Di,檢查該動車組執行該項作業的時段是否與Lj中已存在的動車組執行該項作業的時段存在重疊部分,如果不存在重疊部分,則將動車組Di放入Lj,轉Step 2,否則轉Step 3。 Step 5:檢查是否已將所有動車組放入集合中,如果所有動車組都已放入集合中,則輸出1個調車作業計劃,終止算法;否則轉Step 4。 假設某動車運用所為盡頭式布局,共有4條檢修線(R1-R4),2條清洗線(C1和C2)和10條存車線(S1-S10)。檢修作業時間標準為2.0 h,清洗作業時間標準為0.5 h[1]。動車組運用計劃見表1。 采用建立的模型和給出的算法,選取不同參數對算法進行測試。結果表明,種群規模Z在200~800范圍內調整,正態分布隨機數θ的標準差δ在0.7~1.0范圍內調整,算法均能收斂至相同的最優解。 選取收斂至最優解所需運算時間最小的參數為:種群規模Z=200,最大迭代次數G=1 000,正態分布隨機數θ的標準差δ=0.95,替換不可行個體的替換概率P=0.6。經過10次測算,收斂至最優解的平均計算時間為9.12 s。算法迭代圖如圖3所示。 表1 某動車運用所運用計劃 圖3 算法迭代圖 圖3給出了算法的最快、最慢和平均搜索過程,其中右上圖是第38代至第800代的局部放大圖。最小延誤為0,最快在第108代收斂至最優解,最慢在第794代收斂至最優解。最終計算結果見表2。 表2 調車作業計劃 由上可知,本文提出的模型與算法可以在較短時間內求得動車運用所調車作業計劃的最優解,實現動車運用所內動車組總延誤時間的最小(本算例中為0)。 在測試過程中,可以求得目標函數值相同(均為0,即總延誤時間為0)的不同調車作業計劃,這說明動車運用所調車作業計劃存在多樣性,不是唯一的。 本文以動車運用所內所有動車組的總延誤時間最小為目標函數,以作業線數目、動車組數目以及動車組執行各項作業的順序和占用作業線的時間為約束條件,構建了動車運用所調車作業計劃優化模型,并用微進化算法和作業線分配算法對模型進行求解,通過迭代逐步得到了問題的最優解。算例的計算結果表明,通過該模型及算法可以實現動車運用所調車作業計劃的自動編制,驗證了模型及算法的有效性。 實際工作中,部分動車運用所的作業線為二列位設計,即1條作業線可以容納1列長編組動車組或2列短編組動車組。對于這種情況,編制動車運用所調車作業計劃還需要考慮動車組的長短編組因素,如何在構建模型時考慮動車組的長短編組情況將是今后研究的一個重點。 [1]王忠凱,史天運,張惟皎,等. 動車運用所調車作業計劃優化編制模型與算法[J]. 鐵道學報,2013,35(8):1-9. (WANG Zhongkai, SHI Tianyun, ZHANG Weijiao, et al. Model and Algorithm for Optimized Formulation of Scheduled Shunting Operation Plans of Electric Multiple Units Depots [J]. Journal of the China Railway Society, 2013, 35(8):1-9. in Chinese) [2]張惟皎,史天運,陳彥. 動車運用所存車線運用方案優化模型與算法[J]. 中國鐵道科學,2013,34(1):121-125. (ZHANG Weijiao, SHI Tianyun, CHEN Yan. Optimization Model and Algorithm for the Operation Plan of the Stabling Track at EMU Running Shed [J]. China Railway Science, 2013, 34(1):121-125. in Chinese) [3]張英貴,雷定猷,劉明翔. 鐵路車站股道運用排序模型與算法[J]. 中國鐵道科學,2010,31(2):96-100. (ZHANG Yinggui, LEI Dingyou, LIU Mingxiang. Scheduling Model and Algorithm for Track Application in Railway Station [J]. China Railway Science, 2010, 31(2):96-100. in Chinese) [4]史峰,陳彥,秦進,等.鐵路客運站到發線運用和接發車進路排列方案綜合優化[J].中國鐵道科學,2009,30(6):108-113. (SHI Feng, CHEN Yan, QIN Jin, et al. Comprehensive Optimization of Arrival-Departure Track Utilization and Inbound-Outbound Route Assignment in Railway Passenger Station [J]. China Railway Science, 2009, 30(6): 108-113. in Chinese) [5]CHEN Dingjun, NI Shaoquan, LI Chengbing, et al. Study on the Optimization Model of Utilization Scheme of Railway Passenger Station Tracks Based on an Improved ACO Algorithm [C]//Second International Conference on Intelligent Computation Technology and Automation. Changsha: IEEE, 2009:415-418. [6]呂紅霞,何大可,陳韜. 基于蟻群算法的客運站到發線運用計劃編制方法[J]. 西南交通大學學報,2008,43(2):153-158. (Lü Hongxia, HE Dake, CHEN Tao. Method of Arrival and Departure Tracks Utilization Plan in Railroad Passenger Station Based on Ant Colony Algorithm [J]. Journal of Southwest Jiaotong University, 2008, 43(2):153-158. in Chinese) [7]SHEN Liji. A Tabu Search Algorithm for the Job Shop Problem with Sequence Dependent Setup Times [J]. Computers & Industrial Engineering, 2014, 78: 95-106. [8]HUANG X W, ZHAO X Y, MA X L. An Improved Genetic Algorithm for Job-Shop Scheduling Problem with Process Sequence Flexibility [J]. International Journal of Simulation Modelling, 2014, 13(4): 510-522. [9]MEERAN S,MORSHED S. A Hybrid Genetic Tabu Search Algorithm for Solving Job Shop Scheduling Problems: A Case Study [J]. Journal of Intelligent Manufacturing, 2012, 23:1063-1078. [10]GIOVANNI L D E, PEZZELLA F. An Improved Genetic Algorithm for the Distributed and Flexible Job-Shop Scheduling Problem [J]. European Journal of Operational Research, 2010, 200: 395-408. [11]CHANDRASEKARAN M, ASOKAN P, KUMANAN S, et al. Solving Job Shop Scheduling Problems Using Artificial Immune System [J]. The International Journal of Advanced Manufacturing Technology, 2006, 31:580-593. [12]PONNAMBALAM S G, ARAVINDAN P, RAJESH S V. A Tabu Search Algorithm for Job Shop Scheduling [J]. The International Journal of Advanced Manufacturing Technology, 2000, 16:765-771. [13]許小健,查日興. 一種新型群體智能優化算法——微進化算法[J]. 廈門理工學院學報,2010,18(3):38-42. (XU Xiaojian, ZHA Rixing. Microevolution Algorithm: a New Swarm Intelligent Optimization [J]. Journal of Xiamen University of Technology, 2010, 18(3):38-42. in Chinese) [14]彭汝發,許小健. 用微進化算法反演巖石蠕變模型非定常參數[J]. 長江科學院院報,2011,28(6):50-54. (PENG Rufa, XU Xiaojian. Microevolution Algorithm for Inversion of Non-Stationary Parameters in Rock Creep Model [J]. Journal of Yangtze River Scientific Research Institute, 2011, 28(6):50-54. in Chinese)3.3 個體狀態的更新方式

3.4 作業起止時刻方案和總延誤時間計算方法
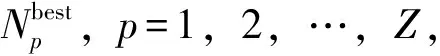
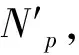
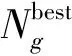
3.5 作業線分配算法
4 算例分析
5 結 語

