基于相關性函數的多傳感器自適應加權融合算法
丁 輝,仲 躍,張 俊,錢建中
(1.安徽工業大學 機械學院,安徽 馬鞍山 243032; 2.鹽城市水利局,江蘇 鹽城 224005;
3.鹽城市鹽都區水務局,江蘇 鹽城 224005)
?
基于相關性函數的多傳感器自適應加權融合算法
丁輝1,仲躍2,張俊3,錢建中2
(1.安徽工業大學 機械學院,安徽 馬鞍山243032; 2.鹽城市水利局,江蘇 鹽城224005;
3.鹽城市鹽都區水務局,江蘇 鹽城224005)
摘要:針對多傳感器實際測量中個別傳感器出現的數據偏離現象,提出基于相關性函數的自適應加權融合算法。利用相關性函數對數據進行預處理,計算各傳感器間的相互支持程度,對于偏離較為明顯的數據,用相關性大的數據進行替換;再通過多傳感器自適應加權融合算法對數據進行融合。利用該算法對相關數據進行處理,經計算分析得到融合結果為0.999 7,并與傳統自適應加權融合算法以及極大似然法的計算結果進行對比。分析結果表明:算法的融合結果更接近實際,融合精度較高。
關鍵詞:多傳感器;自適應加權融合;相關性函數
多傳感器數據融合是將來自多個傳感器的數據或信息采用某種方式進行綜合處理的過程。與單傳感器測量數據相比,融合后的數據更接近被測參數的理論值,效果更佳。隨著傳感器技術等相關技術的發展,多傳感器數據融合技術在軍事領域和民用領域均得到了廣泛應用[1-4]。
目前,模糊推理法[5]、神經網絡法[6]、加權平均法等是應用較為普遍的數據融合方法。例如:黨宏社等[7]將輸入數據和輸出數據模糊化,通過三角形隸屬函數在相應區間內不斷改變輸出變量位置的方法,計算出輸入和輸出兼容度最大的位置,得到最終融合結果;仲崇權等[8]提出了基于最小二乘的加權融合算法,應用最小二乘原理推導出最優加權因子,利用加權算法求得融合結果;翟翌立等[9]從總均方誤差最小這一思想出發,提出了多傳感器自適應加權融合算法。以上方法均獲得了較理想的融合結果,但未考慮傳感器數據采集過程中可能出現偏差的情況。為避免當采集數據出現偏差時降低融合精度的情況發生,需對采集數據進行預處理。對此,本文將模糊數學中的相關性函數和多傳感器自適應加權融合算法相結合,以期在傳感器測量數據出現偏離的情況下,通過對數據進行預處理獲得比較理想的融合結果,提高融合精度。
1相關性函數

(1)
(2)
式中:dij為第i個傳感器與第j個傳感器所測數據的置信距離測度。
假設利用n個傳感器測量某一待測參數,則其置信距離測度dij(i,j=1,2,…,n)構成了這n個傳感器的置信距離矩陣Dn。
(3)
給出融合上限θij,對于dij,令關系系數
(4)
如果rij=0或rji=0,則第i個傳感器和第j個傳感器相互不支持。如果rij=1,則說明第i個傳感器支持第j個傳感器。如果rij=rji=1,則第i個傳感器與第j個傳感器相互支持。
在多傳感器監測系統中,當1組傳感器均支持該傳感器,則該傳感器的測量數據有效;當僅有極少數或沒有傳感器支持該傳感器,則該傳感器的測量數據無效。在進行融合計算時,無效數據可以被同組支持程度最高的傳感器的觀測數據代替。融合上限θij的選取存在主觀性和經驗化,對此,可采用如下方法:
由dij的推算過程和統計意義易知0≤dij≤1,且dij越小,第i個傳感器支持第j個傳感器的程度越高。根據模糊理論中相關性函數的定義[11],可令
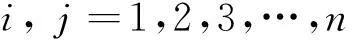
(5)
sij表示傳感器i支持傳感器j的程度。相關性函數gij為
(6)
所有gij構成相關性矩陣Gn。為計算各傳感器被同組傳感器支持程度的大小,定義該傳感器被同組傳感器支持的最低程度作為該傳感器被同組傳感器的支持程度,則令
(7)

2多傳感器自適應加權融合算法

(8)
(9)

(10)
由式(10)可知,總均方誤差為各加權因子的多元二次函數。利用多元函數求解條件極值的方法,可計算出在總均方誤差最小的條件下其最優加權因子為[9]
(11)
采用最優加權因子,計算的最小均方差為
(12)
3計算分析
3.1算法步驟
數據處理的估計算法運算步驟如下:
1) 運用式(1)~(3)計算出測量數據的置信距離矩陣Dn;

3) 比較相關性矩陣各值的大小,對于偏離較為明顯的數據用相關性大的數據替換;
3.2計算結果與分析
采用文獻[10]中的數據,即用10個同類傳感器測量某性能參數(如表1)。為進行對比,利用傳統多傳感器自適應加權算法[9]對以上數據進行融合,求得各傳感器的最優加權因子(如表2)。
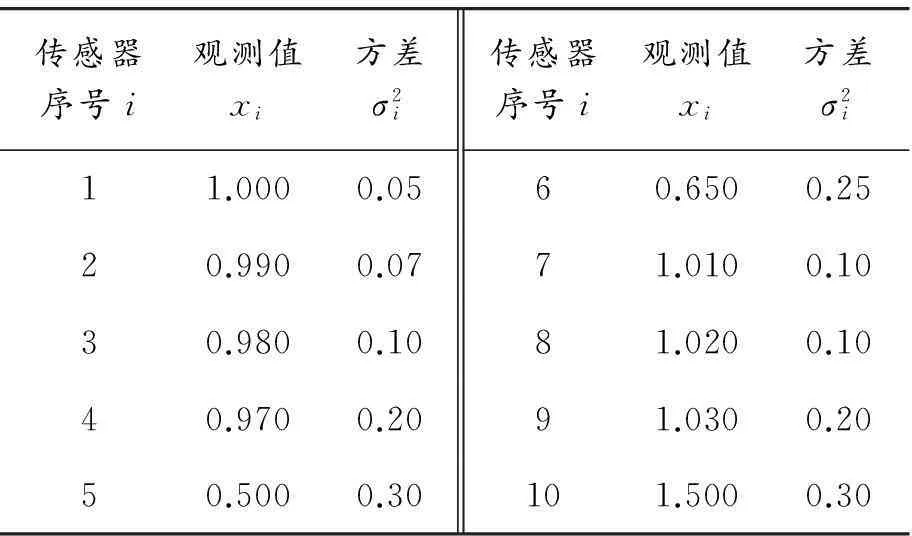
表1 某性能參數計算數據
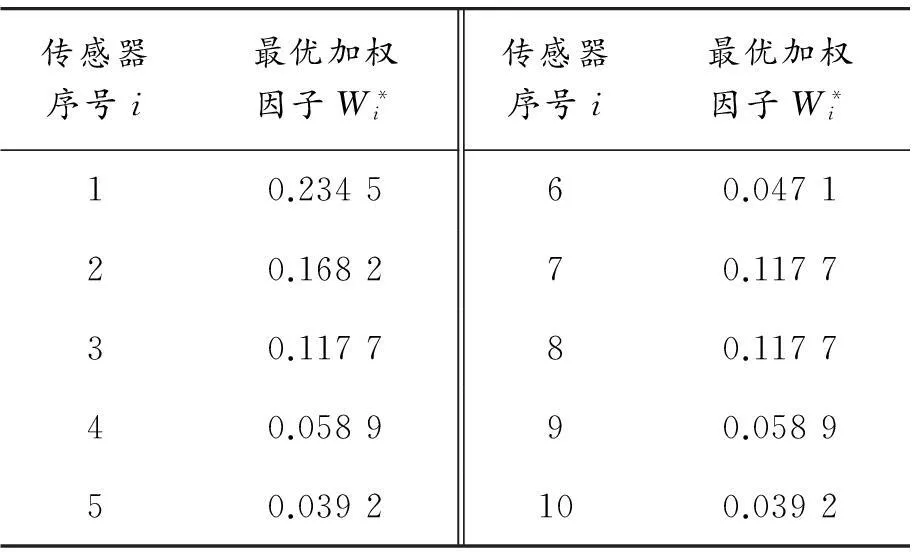
表2 原始數據的最優加權因子
利用文獻[9]中多傳感器自適應加權融合算法的計算結果為
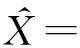
0.98×0.117 7+0.97×0.058 9+
0.50×0.039 2+0.65×0.041 7+
1.01×0.117 7+1.02×0.117 7+
1.03×0.058 9+1.50×0.039 2=0.983 0
利用本文算法進行分析,由步驟1)可得到各傳感器的置信距離矩陣D10:
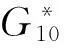
由以上計算值可知:第1個傳感器被其他傳感器支持的程度最高,第5、6個和第10個傳感器被其他傳感器支持的程度較低,因此用第1個傳感器的觀測數據代替這3個傳感器的觀測數據。根據以上分析,表1的計算數據變更為表3。根據表3,由步驟4)計算可得各傳感器的最優加權因子,見表4。
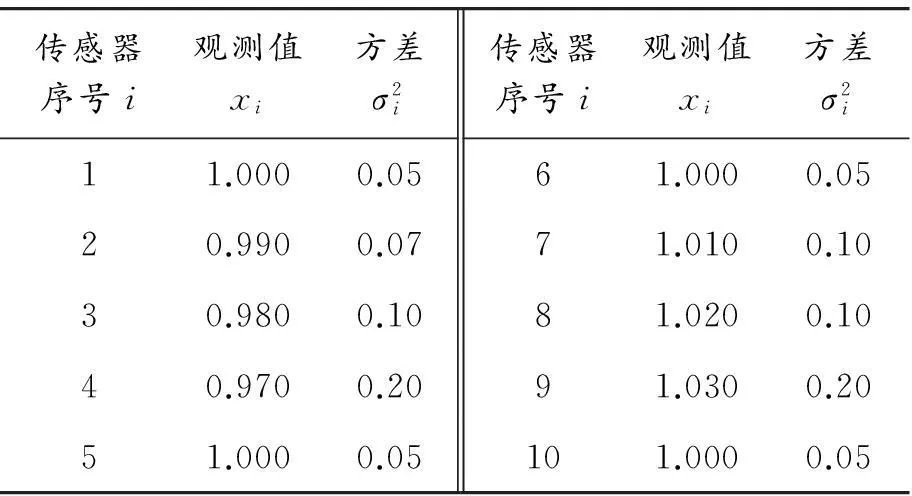
表3 數據預處理后的計算數據
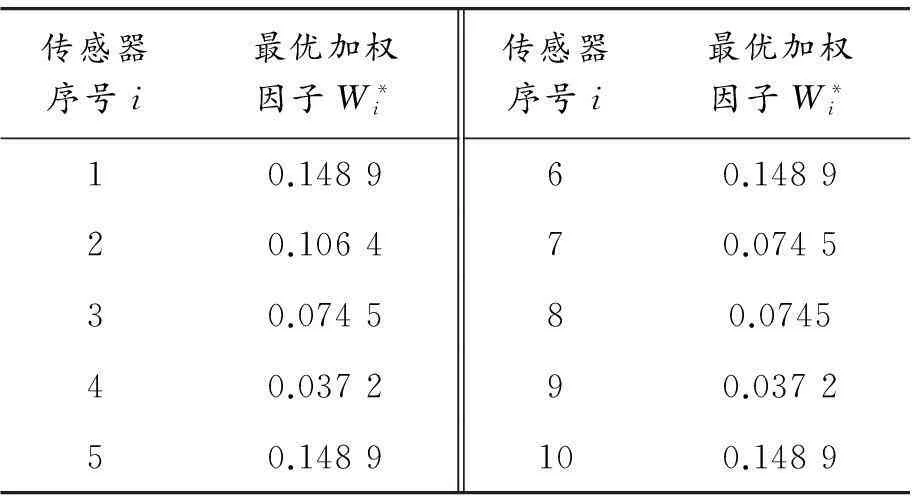
表4 數據預處理后的最優加權因子
根據表3,4,由步驟5)計算可得
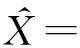
0.98×0.074 5+0.97×0.037 2+
1.00×0.148 9+1.00×0.148 9+
1.01×0.074 5+1.02×0.074 5+
1.03×0.037 2+1.00×0.148 9=0.999 7
由計算結果可以看出:僅利用自適應加權融合算法的融合結果為0.983 0,運用極大似然方法獲得的融合結果為0.999 26[10],而本文方法的融合結果為0.999 7,表明提出的算法融合精度更高。
4結束語
在利用多個傳感器對某一參數進行測量時,針對個別測量數據可能出現偏離的情況,提出基于相關性函數的自適應加權融合算法。利用相關性函數對數據進行預處理,再利用自適應融合算法得到融合結果,并與傳統多傳感器自適應加權融合算法及極大似然方法的融合結果進行對比。結果表明:本文算法的融合結果更接近實際,融合精度更高。
參考文獻:
[1]王耀南,李樹濤.多傳感器信息融合及其應用綜述[J].控制與決策,2001,16(5):518-522.
[2]付華,杜曉坤.基于Bayses估計理論的數據融合方法[J].自動化技術與應用,2005,24(4):10-12.
[3]陳咨余,張新偉,葉凌云.基于LMS算法的多傳感器數據加權融合算法[J].計算機工程與應用,2014,50(20):86-90.
[4]王軍,蘇劍波,席裕庚.多傳感器融合綜述[J].數據采集與處理,2004,19(1):72-77.
[5]李雄,王凱,徐宗昌.基于模糊貼近度的多傳感器數據融合測量[J].計測技術,2005 25(4):6-8.
[6]王曉東,鄔納新,王超,等.連續加熱爐運行狀態神經網絡融合分析[J].安徽工業大學學報(自然科學版),2002,19(4):270-272.
[7]黨宏社,韓崇昭,王立琦,等.基于模糊推理原理的多傳感器數據融合方法[J].儀器儀表學報,2004,25(4):527-530.
[8]仲崇權,張立勇,楊素英,等.基于最小二乘原理的多傳感器加權融合算法[J].儀器儀表學報,2003,24(4):427-430.
[9]翟翌立,戴逸松.多傳感器數據自適應加權融合估計算法的研究[J].計量學報,1998,19(1):1-7.
[10]萬樹平.基于最小一乘估計的多傳感器信息融合方法[J].計算機工程,2010,36(2):257-259.
[11]MAMLOOK R.Fuzzy set methodology for evaluating alternatives to compare between different power production systems[J].Journal of Applied Science,2006,6(9):2117-2125.
(責任編輯楊黎麗)
Multi-Sensor Adaptive Weighted Fusion Algorithm Based on Correlation Function
DING Hui1, ZHONG Yue2, ZHANG Jun3, QIAN Jian-zhong2
(1.School of Mechanical Engineering, Anhui University of Technology, Maanshan 243032, China;2.Yancheng Water Conservancy Bureau, Yancheng 224005, China;3.Yandou Water Conservancy Bureau, Yancheng 224005, China)
Abstract:Aiming at the phenomenon that a sensor may get biased data in the process of multi-sensor measurement, the multi-sensor adaptive weighted fusion algorithm based on correlation function was put forward. The data was preprocessed by correlation function, and then the mutual supportability of each sensor was calculated. In terms of the obvious biased data, they were replaced by high correlation data. Finally, the data was fused by using multi-sensor adaptive weighted fusion algorithm. The related data was processed by using the algorithm. The fusion result, which is 0.999 7, was obtained via calculation and analysis. Moreover, it was compared with traditional adaptive weighted fusion algorithm and maximum likelihood method. The result shows that the fusion result based on the algorithm is close to the real situation and has a higher precision.
Key words:multi-sensor; adaptive weighted fusion; correlation function
文章編號:1674-8425(2016)02-0114-05
中圖分類號:TP274
文獻標識碼:A
doi:10.3969/j.issn.1674-8425(z).2016.02.020
作者簡介:丁輝(1988—),男,安徽阜陽人,碩士研究生,主要從事現代設計方法、多傳感器數據融合研究。
基金項目:江蘇省水利科技項目(2014078)
收稿日期:2015-04-09
引用格式:丁輝,仲躍,張俊,等.基于相關性函數的多傳感器自適應加權融合算法[J].重慶理工大學學報(自然科學版),2016(2):114-118.
Citation format:DING Hui, ZHONG Yue, ZHANG Jun, et al.Multi-Sensor Adaptive Weighted Fusion Algorithm Based on Correlation Function[J].Journal of Chongqing University of Technology(Natural Science),2016(2):114-118.

