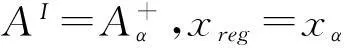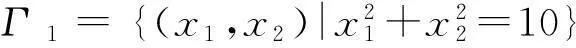彈性邊界條件識別反問題的正則化間接邊界元法

吳月龍，陳學友，張耀明

(山東理工大學 理學院，山東 淄博　255091)

?

彈性邊界條件識別反問題的正則化間接邊界元法

吳月龍，陳學友，張耀明

(山東理工大學 理學院，山東 淄博255091)

摘要：基于間接變量規則化邊界元法，對彈性邊界條件識別Cauchy反問題進行了研究。 對于實施過程中出現的線性病態方程組，采用Tikhonov和TSVD兩種正則化方法求解，通過廣義交叉校驗準則法(GCV法)確定正則化參數。 數值算例表明：該算法穩定，數值解與精確解比較吻合。

關鍵詞：間接邊界元法；反問題；正則化方法；廣義交叉校驗準則法

彈性邊界條件識別反問題是指通過對象部分表面或內部的相關信息，反演物體邊界條件的一類問題。它涉及物理學、數學、實驗技術等多個學科領域，在建筑、機械、化工、航天等工程領域中有著廣泛的應用。

有限差分法(FDM)和有限元法(FEM)已被應用于反問題的研究中，然而，它們均需在物體內部劃分網格，過程繁復，耗費大量計算時間，而且求解精度較差。 邊界元法(BEM)由于只需在物體邊界劃分單元，大大減小了工作難度，提高了計算效率，使其在反問題的研究中更加有效。 已有的反問題研究主要集中在直接變量邊界元法。文獻[1]將直接邊界積分方程結合TSVD法求解各向同性二維彈性力學Cauchy問題，并通過L曲線法選取參數。文獻[2]將直接邊界積分方程結合預處理共軛梯度法求解二維各向同性彈性力學邊界條件識別反問題。本文基于文獻[3-4]提出的間接變量規則化邊界積分方程，對二維彈性力學邊界條件識別反問題進行了研究.

在反問題求解過程中，相應的線性系統通常是嚴重病態的，直接使用傳統的Gauss消去法一般很難獲得其有效解，因此采用適當的正則化方法求解是必要的。最常用的正則化方法有Tikhonov法、TSVD法及PCG法(預處理共軛梯度法)[2]。 確定正則化參數的常用方法有L曲線法、GCV法(廣義交叉校驗準則)及波動曲線法等[5-6]。本文采用Tikhonov和TSVD 2種正則化方法來求解病態線性系統。正則化參數的選取通過GCV法來完成。 數值算例表明：本文算法穩定，數值結果與精確解比較吻合。

1反問題及規則化邊界積分方程

1.1二維彈性邊界條件識別反問題

設：Ω是R2上的一個有界區域；Γ=?Ω是其邊界；t(x)、n(x)是邊界Γ在點x處的單位切、外法向量。Γ由Γ1、Γ2兩部分組成，且Γ=Γ1∪Γ2，Γ1,Γ2≠?，Γ1∩Γ2=?。

本文考慮子邊界Γ1上面力和位移已知、Γ2上面力和位移均未知的邊界條件識別反問題，如圖1所示。

圖1　Cauchy型彈性邊界條件識別反問題

1.2規則化邊界積分方程

二維彈性問題的等價的規則化間接變量邊界積分方程為[3]：

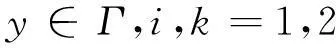
(1)

▽yui(y) =

(2)

特別地

pi(y)=

(3)

其中，位移基本解

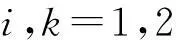
(4)

面力基本解

(5)

2正則化方法

2.1奇異值分解(SVD)

對于線性方程組

Ax=b

1288 Research focus of critical care medicine: a study based on Web of Science retrieve and bibliometrics

(6)

其中：A∈Rm×n，x∈Rn，b∈Rm，且m≥n。對矩陣A進行奇異值分解，則有

且

UUT=Im∈Rm×m,VVT=In∈Rn×n,

m≥n,σ1≥…≥σp>0,σp+1=…=σn=0

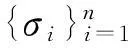
方程(6)的解可用Moore-Penrose廣義逆A+來表示，

(7)

2.2Tikhonov正則化方法(TR)

Tikhonov正則化方法[5]構造了一種依賴于參數α>0的泛函：

(8)

可通過求解該泛函的極小值得到式(8)的一個較好的近似解。顯然，對于任意α>0，Jα是嚴格凸的，因此有唯一的xα滿足

此時xα即為Jα的正則解。而xα又是方程

的解，且ATA+α2In對稱正定，所以該方程的解唯一，可表示為

2.3截斷奇異值分解法(TSVD)

對于方程組(6)、式(7)中x的歐幾里得范數可寫為

其中rε為滿足1

k≤p即為正則化參數，其對應的截斷奇異值解為

2.4廣義交叉檢驗準則(GCV)

廣義交叉檢驗準是由Golub.G.H.提出的，其基本思想：假定將任意一個觀測值bi從原觀測值序列b中刪除，則此時由剩余觀測值求得的正則化解應能夠較好地預測b中被去掉的這一觀測值bi。廣義交叉檢驗法可以等效為求解最小GCV函數問題：

3數值算例

計算時，內、外邊界分別被等分成20個和40個精確單元，邊界量采用不連續線性插值[3]。用Tikhonov和TSVD兩種正則化方法求解線性系統，并用GCV法選取正則化參數。圖3、4表明：兩種方法分別在α=1.0e-06和k=165處達到GCV最小值，因此選取上述參數作為該問題的正則化參數。 圖5描述了在選取前述正則參數的情形下，通過兩種正則化方法求得的邊界位移數值解及與解析解的比較。圖6描述了在選取前述正則參數的情形下，通過兩種正則化方法求得的邊界面力數值解及與解析解的比較。從圖5、6可以看出：數值解與解析解比較吻合，表明間接邊界積分方程結合正則化方法能夠有效地求解二維彈性反問題。

圖3　GCV法選取Tikhonov正則化參數

圖4　GCV法選取TSVD正則化參數

4結束語

二維彈性問題邊界條件反識別問題具有不適定性，求解中涉及的線性系統是高度病態的，因此常規邊界元法直接求解此問題時已經失效。本文運用間接規則化邊界元方法，結合Tikhonov和TSVD兩種正則化措施，通過GCV法確定Tikhonov法的最優參數和TSVD法的最佳截斷項，有效地解決了這個問題。通過數值算例驗證了該方法的有效性。

參考文獻：

[1]周煥林,江偉,胡豪.二維彈性力學邊界條件反識別TSVD正則化法[J].合肥工業大學學報(自然科學版),2013,36(9):1076-1081.

[2]周煥林,江偉,胡豪.二維彈性力學邊界條件反識別PCG正則化法[J].固體力學學報,2013,33(10):288-293.

[3]張耀明,溫衛東,王利民.彈性力學平面問題中一類無奇異邊界積分方程[J].力學學報,2004,36(3):311-321.

[4]ZHANG Y M,LIU Z Y,GAO X W,et al.A novel boundary element approach for solving the 2D elasticity problems[J].Applied Mathematics and Computation,2014; 232(3):568-580.

[5]TIKHONOV A N,ARSENIN V Y.Solutions of ill-Posed Problem[M].New York:John Wiley and Sons.1977.

[6]HANSEN P C.Analysis of discrete ill-posed problems by means of the L-curve[J].SIAM Review,1992,34(4):561-580.

(責任編輯陳艷)

Regularized Boundary Element Method with Indirect Unknowns for Inverse Elasticity Problems

WU Yue-long, CHEN Xue-you, ZHANG Yao-ming

(School of Science, Shandong University of Technology, Zibo 255091, China)

Abstract:The elasticity inverse identification boundary conditions Cauchy problem was investigated by using the indirect boundary element method (IBEM). Both the Tikhonov regularization method and the truncated singular value decomposition (TSVD) were applied to solving the ill-conditioned linear system involved in the process of implementation, and the optimal parameter for the Tikhonov and the optimal truncation number for the TSVD were chosen according to the generalized cross validation(GCV) method. A numerical example was given to verify the effectiveness of the proposed scheme, with numerical results being good agreement with the exact solutions.

Key words:indirect boundary element method; inverse problem; regularization method; generalized cross validation method

文章編號：1674-8425(2016)02-0152-05

中圖分類號：O343.1

文獻標識碼：A

doi:10.3969/j.issn.1674-8425(z).2016.02.026

作者簡介：吳月龍(1991—),男,山東聊城人,碩士研究生,主要從事計算數學研究。

基金項目：山東省自然科學基金資助項目(ZR2010AZ003)

收稿日期：2015-08-28

引用格式：吳月龍，陳學友，張耀明.彈性邊界條件識別反問題的正則化間接邊界元法[J].重慶理工大學學報(自然科學版)，2016(2):152-156.

Citation format：WU Yue-long, CHEN Xue-you, ZHANG Yao-ming.Regularized Boundary Element Method with Indirect Unknowns for Inverse Elasticity Problems[J].Journal of Chongqing University of Technology(Natural Science)，2016(2):152-156.