基于服務網絡動態配流的直達列車開行方案優化編制方法

唐金金，楊露萍,周磊山

(1.北京交通大學 交通運輸學院，北京　100044；2.中國鐵道科學研究院 運輸及經濟研究所，北京　100081)

鐵路車流組織是指確定車流在鐵路網絡上的運行徑路、直達列車開行方案以及車流改編方案等[1]。由于鐵路路網規模龐大、車站數量多、OD車流方向眾多、車流和列車流繁多，使得運行徑路、直達列車開行方案以及車流改編方案均非常龐大，國內外眾多專家學者論證了該問題是NP-Hard問題。因此，實際鐵路車流組織過程中，將鐵路車流組織優化問題分解為2步，第1步是車流徑路優化，第2步是貨物列車編組計劃優化，其中直達列車開行方案優化是其核心。文獻[2]研究了鐵路路網上車流徑路優化的0-1規劃模型及其合理徑路生成算法。文獻[2—11]嘗試用精確算法求解列車編組計劃優化編制問題，但是難以求解大規模網絡問題。文獻[12—13]采用模擬退火等啟發式算法求解了大規模編組計劃優化編制問題。然而既有列車編組計劃優化編制模型和求解算法中依然存在2個難點難以克服。一是既有文獻假設車流集結參數為固定值，而實際集結參數應為變量；二是在求解大規模路網的編組計劃優化編制問題時，算法求解時間依然過長，難以滿足鐵路運輸部門實際應用要求。

為此，本文將編組計劃中的直達列車開行方案優化編制問題轉化為網絡設計中的服務網絡動態配流問題。具體方法是根據所有可能的直達開行方案構建服務網絡；參考道路交通中車流與能力關系的BPR函數，進一步構建路段旅行費用與車流量的關系函數，從而將車流集結參數函數化；基于服務網絡動態配流算法，實現服務網絡流的平衡；此時服務網絡中存在車流量的方案弧則表示對應編組站間需要開行直達列車，所有需要開行的直達列車即組成優化的直達列車開行方案。以某地區鐵路網絡為例，驗證本方法的可行性和有效性。

1　根據所有可能的直達列車開行方案構建服務網絡的方法

根據所有可能的直達列車開行方案構建服務網絡的核心思想：①將編組站視為服務網絡節點，編組站間可開行的直達去向視為節點間有向弧，并將該有向弧作為方案弧，將該直達去向車流的集結時間和旅行時間之和作為方案弧的旅行費用；②將服務網絡節點進一步分解成入流節點和出流節點，其中終到車流到達入流節點則停止，始發車流在出流節點集結，通過車流于入流節點進入并在出流節點集結，從而有效地將車站的終到、始發和通過這3種車流分離；③同一節點的入流節點至出流節點間構造1條有向弧，將該有向弧作為解體弧，供通過車流解體使用，并將車流的解體時間作為解體弧的旅行費用。

為了較好地描述該問題，選取如圖1所示的包含4個編組站的鐵路線路進行描述。其對應的包含全部可能直達去向的開行方案如圖2所示。將這4個編組站作為服務網絡的節點，將對應的直達去向作為節點間的方案弧，則可構造出如圖3所示的服務網絡。

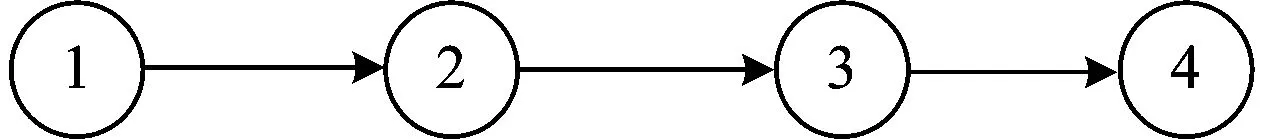
圖1包含4個編組站的鐵路線路

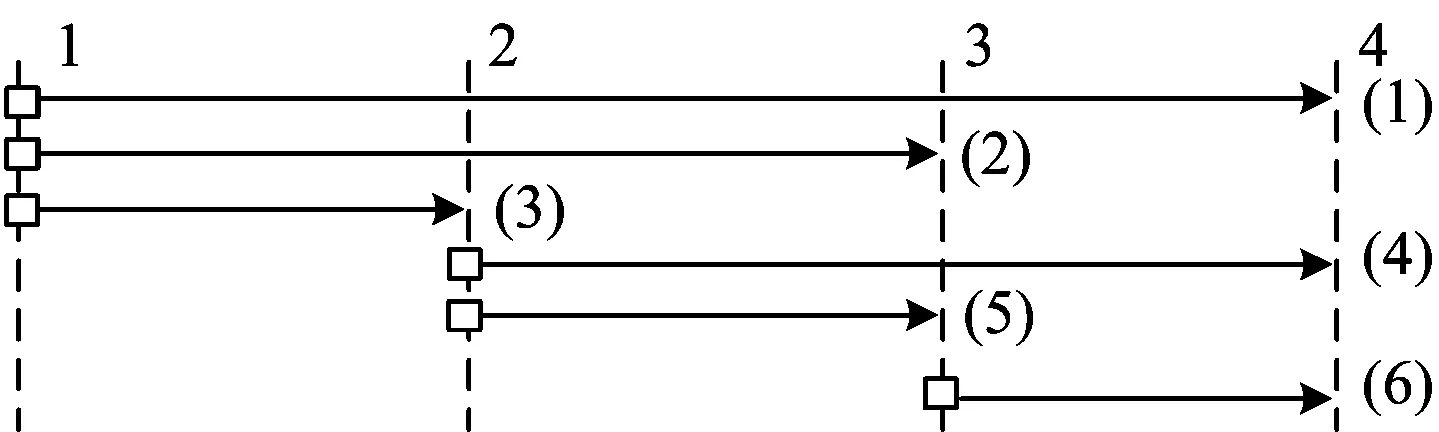
圖2　包含全部可能直達去向的直達列車開行方案

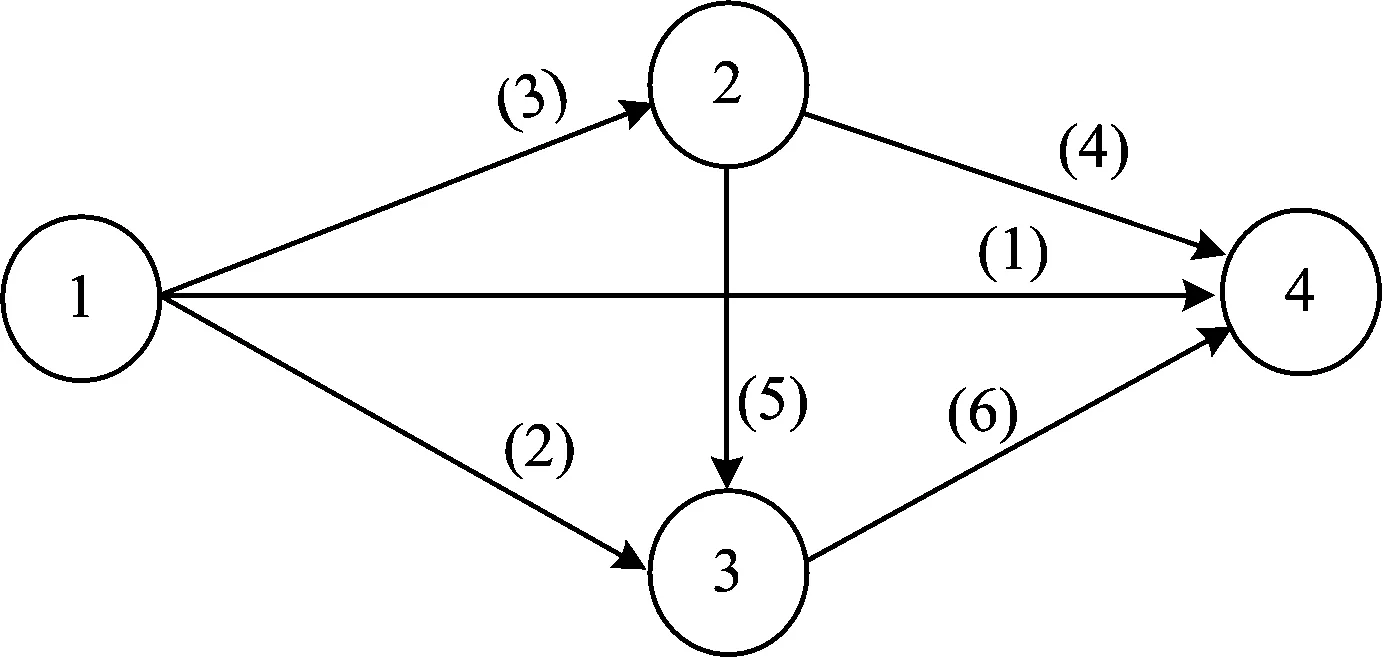
圖3　包含所有直達去向的服務網絡

將圖3中的各節點進一步分為入流節點和出流節點，并在入流節點至出流節點間構造有向弧，將此有向弧作為解體弧，則構建的最終服務網絡如圖4所示。圖4中，入流節點的編號仍采用原節點的編號，出流節點的編號采用在原節點編號的后面加“01”的形式，如鐵路網中的編組站1，則其節點編號和入流節點編號均為1，而出流節點編號為101，從而便于表述節點間的關系。

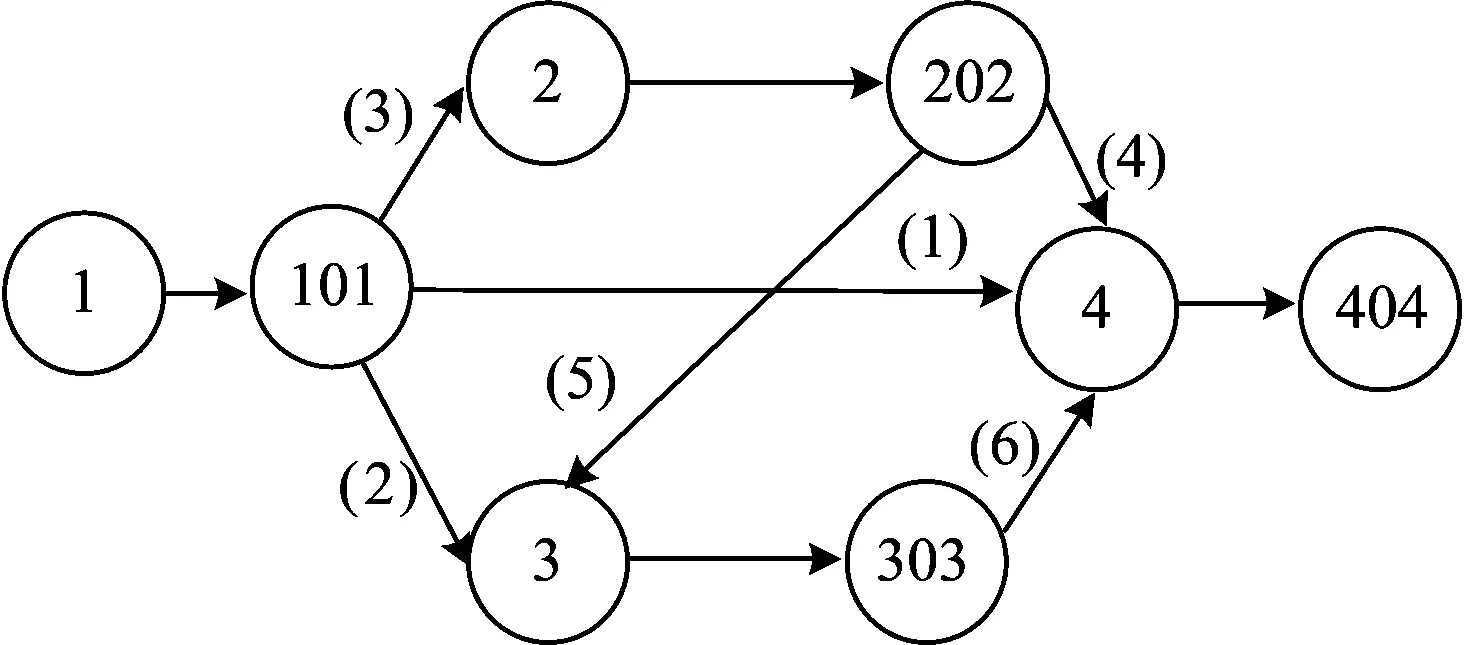
圖4　包含方案弧和解體弧的最終服務網絡

但是，實際直達列車開行方案中不可能包含所有可能的直達去向，而是依據設定的目標函數，在所有的直達去向中選擇某些直達去向，組成優化的直達列車開行方案。

2　服務網絡動態配流的優化模型

定義φ(i，k)為0-1變量，表示弧k是否為編組站i對應的解體弧，若是則φ(i，k)=1， 否則φ(i，k)=0。θ(l，k)為0-1變量，表示弧k是否經由區段l，若是則θ(l，k)=1， 否則θ(l，k)=0。

定義xq，k為0-1決策變量，表示貨車q是否用弧k運輸，若是則xq，k=1， 否則xq，k=0。yi，j為0-1決策變量，表示i至j間是否開行直達列車，若是則yi，j=1，否則yi，j=0。

(1)

以全網絡車流總旅行費用最小為目標函數，構建的服務網絡動態配流優化模型為

(2)

s.t.

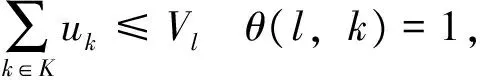
(3)

wi≤Wiφ(i，k)=1， ?i，?k

(4)

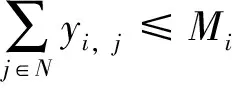
(5)

約束條件中：式(3)為區段通過能力約束，即經由區段l的所有車流量之和應不大于該區段的通過能力；式(4)為編組站改編能力約束，即需要在編組站i改編的所有車流量之和應不大于該編組站的解體能力；式(5)為編組站的編發去向數總數約束，即經由編組站i需要改編的車流方向總數應不大于該編組站規定的最大去向數。

另外，通常在直達列車開行方案優化編制模型當中，還應有車流組織方案唯一性約束，即保證每支車流都有列車將其送達前方編組站改編約束。但在本文中，由于將直達列車開行方案優化編制問題轉化成了服務網絡動態配流問題，這2類約束在車流分配過程中可以自動完成，無需再考慮，因此，本文方法更加簡潔。

3　動態配流優化模型的求解算法

Wardrop于1952年提出了交通網絡配流的2個基本原則[14]，即用戶最優和系統最優。用戶最優是指根據個體旅行費用最小選擇最短徑路，再根據最短徑路進行配流；系統最優是指根據全體用戶旅行費用之和最小進行配流。其他專家在后續的研究中論證了用戶最優和系統最優這2個原則的合理性[15]。

本文所構建的服務網絡與交通網絡類似，求解動態配流優化模型的核心算法是通過仿真的方法，基于用戶最優的原則進行服務網絡配流，最終實現網絡流量的平衡。該方法是：基于單個貨車旅行費用最小選擇最短徑路，當所有貨車實現最短徑路后就完成了1次配流；由于徑路上的車流量直接影響該徑路的旅行費用，因此完成1次配流后，需要重新計算路段旅行費用并對所有貨車進行最短徑路計算，如果本次計算的貨車最短徑路與上一次配流過程對應的最短徑路不一致，那么網絡流量沒有達到平衡，則以當前網絡旅行費用為基礎再次進行配流；通過多次迭代仿真計算，使得所有貨車在路網上的旅行總費用最少，服務網絡中車流量達到平衡，從而完成服務網絡配流。設計的求解算法框圖如圖5所示。

算法過程分為2步：第1步，基于服務網絡，計算任意OD車流間的最短徑路，依據最短徑路將車流分配到服務網絡上；第2步，判斷服務網絡上車流是否達到平衡，如果沒有達到，則繼續第1步，否則，計算完成，得到最優方案。

定義算法中的參數：ε為平衡性判定參數，ε=0表示網絡流量沒有達到平衡，ε=1表示網絡流量達到平衡；δ為當有向弧容量超出其能力時其旅行費用的提升倍數，通常設其值為δ>3。

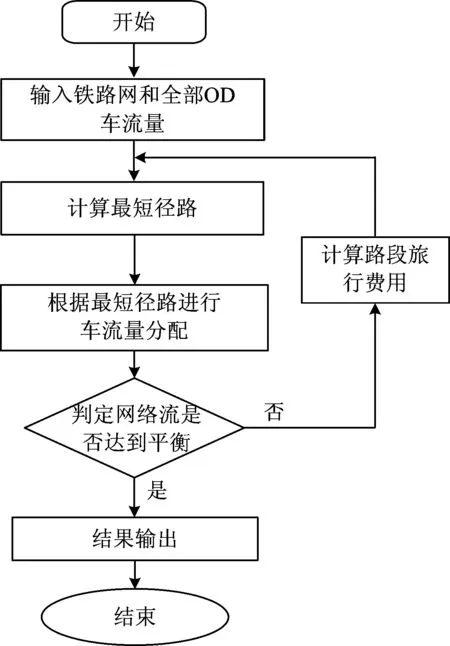
圖5　算法框圖

由此設計的模型求解算法步驟如下。

輸入: 鐵路網G，全部OD車流量。

輸出: 直達列車開行優化方案。

步驟1：初始化。

步驟1.1： 依據鐵路網和所有OD車流，生成包含所有可能直達去向的初始直達列車開行方案。

步驟1.2： 依據鐵路網和初始直達列車開行方案構造服務網絡；設定δ值，令ε=0。

步驟1.3： 以編組站間旅行時間為旅行費用，求解任意OD車流間最短徑路，實現初始配流。

步驟1.4： 如果有向弧的流量為0，則設定該有向弧的流量為0.000 1，從而避免計算中產生無窮大數。

步驟2： 動態配流優化過程。

While (ε=1)

步驟2.1： 依據式(1)計算所有有向弧的旅行費用ck。

步驟2.2： 依據式(3)判定所有區段的流量是否超出其通過能力。如果不超出，則步驟2.3；否則提高對應方案弧的旅行費用δ倍，轉步驟2.3。

步驟2.3： 依據式(5)判定任意編組站i需要改編的車流方向總數是否超過其規定的最大編組去向數Mi。如果不超出，則轉步驟2.4；否則提高對應解體弧的旅行費用δ倍，轉步驟2.4。

步驟2.4： 依據式(4)判定所有編組站的改編車流量是否超出其改編能力。如果不超出，則轉步驟2.5；否則提高對應解體弧的旅行費用δ倍，轉步驟2.5。

步驟2.5： 計算所有貨車在服務網絡上的最短徑路，根據本次最短徑路進行配流。

步驟2.6： 判定所有貨車在服務網絡上的最短徑路與上一次配流的最短徑路是否全部一致，如果存在不一致，那么服務網絡就沒有達到平衡，則令ε=0；否則，表明網絡流量平衡，令ε=1。

End while

步驟3： 得到服務網絡平衡配流的結果后，抽取有流量的方案弧，生成優化的直達列車開行方案。

步驟4： 結束計算，保存數據，輸出優化的直達列車開行方案。

4　實例應用

為了驗證本文所提出的直達列車開行方案優化編制方法的可行性與先進性，選取文獻[12]中的案例進行對比分析，該案例中的鐵路網有19個編組站，如圖6所示。假設編組站平均解體時間為3 h，OD車流量表與其他參數詳見文獻[12]。

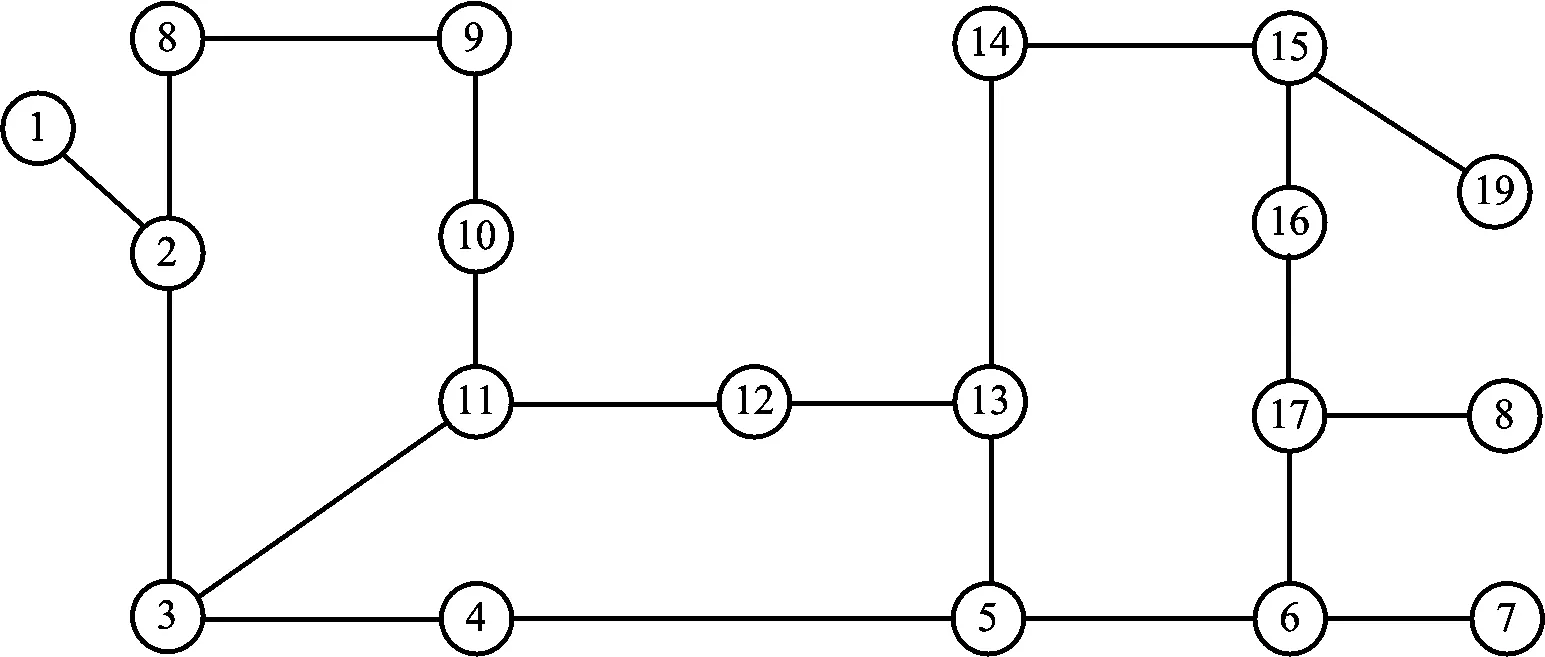
圖6　某區域鐵路網

按照本文方法，依據鐵路網結構和OD車流量，構建的包含方案弧和解體弧的服務網絡如圖7所示。

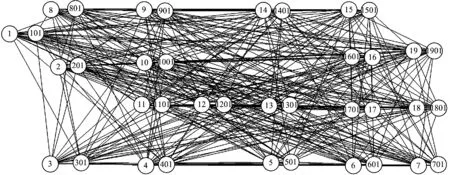
圖7　包含方案弧和解體弧的服務網絡

將本文提出的方法用C# 2010編程實現。在CPU為Inter Core i7 2.8 GHZ，內存為4.0 GB，操縱系統為Windows Sever 2008條件下，對上述案例進行服務網絡動態配流，經過30次迭代達到網絡流量的平衡，完成全部配流過程耗時58 s。得到的直達列車開行優化方案為：總旅行費用39 062車小時，共有66個直達去向，見表1和圖8。由于直達去向較多，為了直觀，圖8中僅顯示了編組站2開行的直達列車開行方案，包括2-1,2-3,

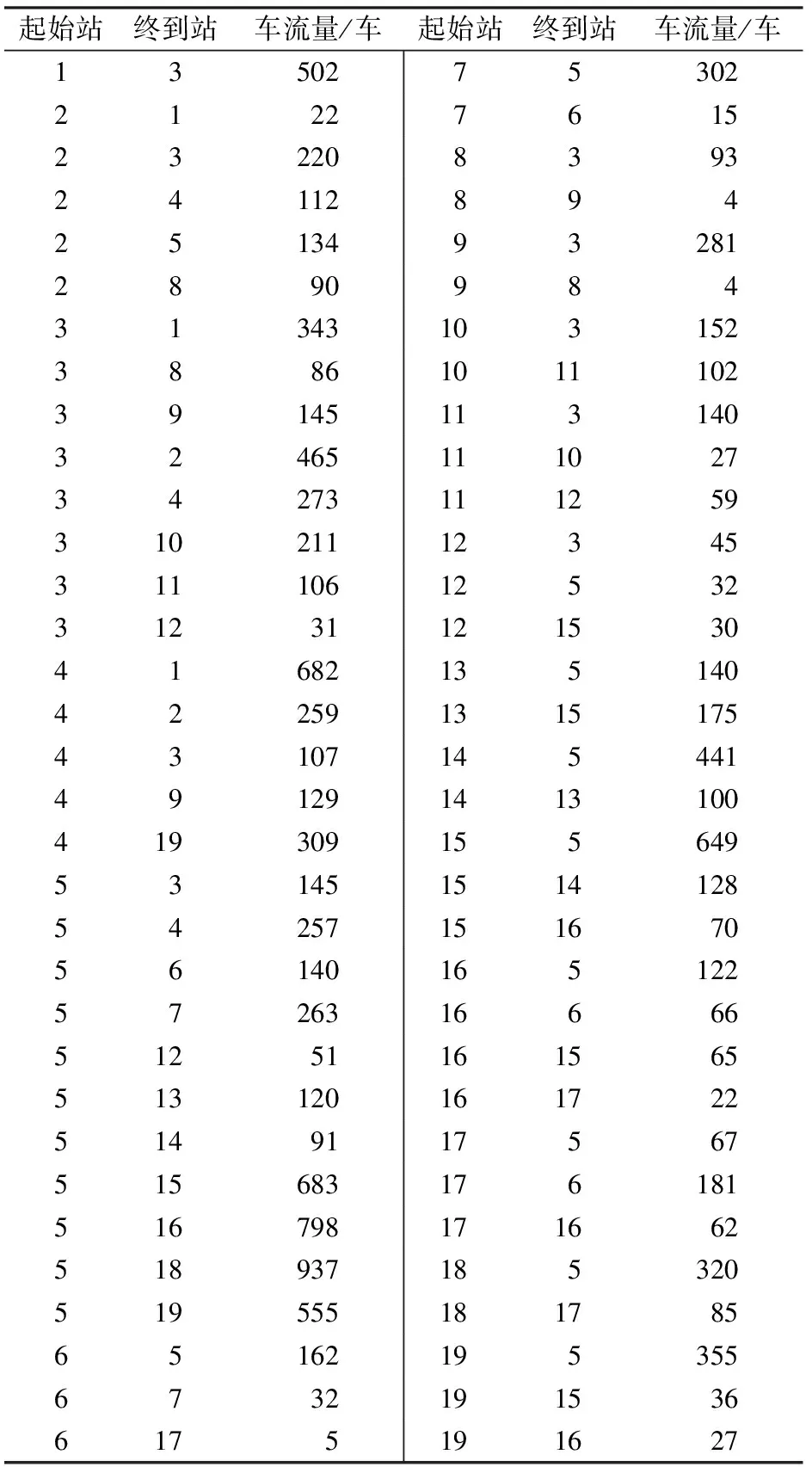
表1　優化解結果

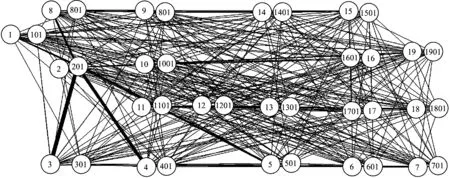
圖8　服務網絡動態配流計算結果

2-4,2-5,2-8，寬的線條表示該方案弧存在車流。

文獻[12]計算得到的直達列車開行優化方案為：總旅行費用45 421車小時，共有69個直達去向。對比本文的與文獻[12]的計算結果可知：本文方案的總旅行費用節省11%，少開行3個直達去向，可見本文的優化效果優于文獻[12]。

截止到2014年12月，全路有40個編組站[16]。可見本文選取有19個編組站的網絡是有一定代表性的。

5　結　語

本文提出了利用服務網絡動態配流方法解決直達列車開行方案優化編制問題。重點研究如何將直達列車開行方案優化編制問題轉化為服務網絡動態配流優化問題的方法，并構建了全新的服務網絡動態配流模型，將直達車流集結車小時消耗與車流在各編組站內改編車小時消耗統一轉化為車流在有向弧上的旅行費用。運用動態配流算法實現網絡流平衡，從而得出優化的直達列車開行方案。以我國某區域鐵路網為例，對比分析了基于服務網絡動態配流的直達列車開行方案優化編制方法與既有方法的優劣，計算結果表明，采用本文方法能夠快速、準確地得到優化的直達列車開行方案。

[1]楊浩, 何世偉. 鐵路運輸組織學[M].3版. 北京:中國鐵道出版社, 2011: 203-244.

(YANG Hao, HE Shiwei. Transportation Organization of Railway [M].3rd ed.Beijing: China Railway Publishing House， 2011: 203-244. in Chinese)

[2]林柏梁, 朱松年,陳竹生, 等. 路網上車流徑路優化的0-1規劃模型及其合理徑路集生成算法[J]. 鐵道學報,1997,19(1): 7-12.

(LIN Boliang, ZHU Songnian, CHEN Zhusheng, et al. The 0-1 Integer Programming Model for Optimal Car Routing Problem and Algorithm for the Available Set in Rail Network [J]. Journal of the China Railway Society, 1997,19(1): 7-12. in Chinese.)

[3]HARRY N Newton，CYNTHIA Barnhart，PAMELA H Vance. Constructing Railroad Blocking Plans to Minimize Handling Costs [J]. Transportation Science, 1998, 32(4): 330-345.

[4]CYNTHIA Barnhart，HONG Jin，PAMELA H Vance. Railroad Blocking: a Network Design Application [J].Operations Research, 2000, 48(4): 603-614.

[5]RAVINDRA K Ahuja，KRISHNA C Jha，JIAN Liu. Solving Real-Life Railroad Blocking Problems [J]. Interfaces, 2007, 37(5): 404-419.

[6]彭其淵, 閆海峰, 周勇. 集裝箱班列編組計劃相關因素分析[J]. 中國鐵道科學, 2003,24(5):120-123.

(PENG Qiyuan, YAN Haifeng, ZHOU Yong. Analysis of Factors Relevant to Formation Plan of Container Blocks [J]. China Railway Science, 2003, 24(5):120-123. in Chinese)

[7]閆海峰, 彭其淵, 譚云江. 結點站間集裝箱班列開行方案的優化模型及算法[J]. 中國鐵道科學, 2008, 29(1): 97-101.

(YAN Haifeng, PENG Qiyuan, TAN Yunjiang. Optimization Model and Algorithm of Block Container Trains Formation Plan between Railway Network Container Freight Stations [J]. China Railway Science, 2008, 29(1): 97-101. in Chinese)

[8]陳崇雙, 王慈光, 薛鋒, 等. 貨物列車編組計劃國內外研究綜述[J]. 鐵道學報, 2012, 34(2): 8-20.

(CHEN Chongshuang, WANG Ciguang, XUE Feng, et al. Survey of Optimization of Train Formation Plan at Home and Abroad [J]. Journal of the China Railway Society, 2012, 34(2): 8-20. in Chinese)

[9]史峰, 李致中, 孫焰, 等. 列車編組計劃網絡優化方法[J]. 鐵道學報, 1994, 16(2): 74-79.

(SHI Feng, LI Zhizhong, SUN Yan, et al. A Network Optimizing Method for the Train Formation Plan [J]. Journal of the China Railway Society, 1994, 16(2): 74-79. in Chinese)

[10]王志美, 林柏梁, 陳雷, 等. 多點列車編組計劃優化模型研究[J]. 中國鐵道科學, 2012, 33(6):108-114.

(WANG Zhimei, LIN Boliang, CHEN Lei, et al. Research on the Optimization Model for Multi-Point Train Formation Plan [J]. China Railway Science, 2012, 33(6): 108-114. in Chinese)

[11]陳崇雙, 王慈光. 分組列車優化組織理論與方法研究[J]. 中國鐵道科學, 2015, 36(2):142-144.

(CHEN Chongshuang, WANG Ciguang. Research on Optimized Organization Theory and Method for Multi-Block Train [J]. China Railway Science, 2015, 36(2): 142-144. in Chinese)

[12]LIN Boliang, WANG Zhimei, JI Lijun, et al. Optimizing the Freight Train Connection Service Network of a Large-Scale Rail System [J]. Transportation Research Part B Methodological, 2012, 46(5):649-667.

[13]林柏梁, 田亞明, 王志美. 基于最遠站法則的列車編組計劃優化雙層規劃模型[J]. 中國鐵道科學, 2011, 32(5):108-113.

(LIN Boliang, TIAN Yaming, WANG Zhimei. The Bi-Level Programming Model for Optimizing Train Formation Plan and Technical Station Load Distribution Based on the Remote Re-Classification Rule [J]. China Railway Science, 2011, 32(5):108-113. in Chinese)

[14]WARDROP J G. Some Theoretical Aspects of Road Traffic Research [J]. Proceeding of the Institution of Civil Engineering， 1952,1(2): 325-378.

[15]BECKMANN Martin J, MCGUIRE C B, WINSTEN Christopher B, et al. Studies in the Economics of Transportation [J]. Economic Journal, 1955, 26(12):820-821.

[16]彭開宇. 中國鐵道年鑒[M]. 北京:中國鐵道出版社, 2014：127-129.

(PENG Kaiyu. China Railway Yearbook[M]. Beijing: China Railway Publishing House, 2014：127-129. in Chinese)