生成高精度軌道電子地圖的數據處理方法

左自輝，王開鋒，許　聰，劉春雨

(1.中國鐵道科學研究院 鐵道科學技術研究發展中心，北京　100081；2.中國鐵道科學研究院 通信信號研究所，北京　100081)

高精度的軌道電子地圖在列車定位、工務養護、通信運營維護等方面具有重要作用，比如利用電子地圖的可視化特點，可以直觀地顯示線路、橋梁、隧道、車站等設施，為鐵路運營維護提供準確的空間分析手段。由于采用鐵路傳統的測量方法難以獲取軌道電子地圖所需的大量基礎數據，近年來，基于全球導航衛星系統(Global Navigation Satellite System，GNSS)的定位技術憑借著其操作簡便、效率高的優勢，逐漸成為采集軌道定位數據的主流方式之一。為此，有關學者對基于GNSS技術的定位問題進行了研究。Robert Libbrecht等研究了基于衛星定位的故障安全型列車定位系統[1]，針對低運量線路提出了軌道電子地圖的生成算法和生成規范，采用列車上裝設的全球定位系統(Global Position System，GPS)設備進行線路數據測繪，最終合成數字軌道地圖；但由于測量數據易受到各種隨機噪聲的干擾，使得測量數據的可靠性和可用性下降。K. Tysen Mueller研究了滿足列車控制系統(Positive Train Control，PTC)精確定位需求的列車定位方法[2]，該方法不但要采集GPS信息，還需要結合加速度計、光纖陀螺和轉速計測出的列車加速度、列車速度，進行精確計算分析，方能得到準確的列車位置信息，方法較為復雜。

本文提出1種生成高精度軌道電子地圖的數據處理方法，該方法采用卡爾曼濾波算法分別對運用GNSS車載設備多次采集到的同一條線路的軌道定位數據進行濾波，剔除采集信息中的野值，從而生成對應該線路的多條軌道曲線；采用軌跡擬合方法對這些軌道曲線進行歸一化處理，生成1條軌道擬合曲線；采用垂直距離判據數據約簡算法去除軌道擬合曲線中的冗余數據；結合地理信息系統技術最終生成該線路的軌道電子地圖，并通過現場試驗數據驗證該方法的合理性和可行性。

1　軌道定位數據特點

利用GNSS技術獲取軌道定位數據時，由于衛星的星歷及時鐘的誤差、用戶接收機精度的誤差、電離層信號的傳播延遲及多路徑效應、地球自轉的影響等，使得衛星信號、傳輸信號和地面設備接收的信息均有誤差，所以GPS單機的定位精度僅為10～15 m(95%置信度)[3]。鐵路線路較長，沿線會穿越城市、平原、高山和河流等，這些環境因素也會導致GNSS系統獲取的軌道定位數據出現野值。

采用GNSS車載設備采集軌道定位數據時，一般根據最困難區段(例如最小曲線半徑區段)的定位精度需求設置采樣頻率，在列車行進過程中均勻地采集軌道定位數據。一方面，鐵路線路較長，采集的軌道定位數據量巨大；另一方面，鐵路線路包括直線、緩和曲線和曲線，其中直線區段和緩和曲線區段可以使用較少的定位點進行定位，因此這些區段的定位數據中包含了大量的冗余數據。

由此可見，若將利用GNSS技術所獲取的軌道定位數據直接用于生成軌道電子地圖，則地圖的精度不夠，且不利于存儲和檢索，因此，需要對數據進行處理。

2　數據處理流程及方法

2.1　數據處理流程

生成高精度軌道電子地圖的數據處理分為4步：第1步，針對GNSS車載設備多次采集的軌道定位數據，采用卡爾曼濾波方法對每次采集的信息進行濾波，消除采集信息中的野值，從而生成多條軌道曲線；第2步，采用軌跡擬合方法，對多條軌道曲線進行歸一化處理，生成1條軌道擬合曲線；第3步，采用垂直距離判據數據約簡算法，去除軌道擬合曲線中的冗余數據；第4步，結合GIS(Geographic Information Systems，地理信息系統)技術，生成軌道電子地圖。數據處理流程如圖1所示。

圖1　數據處理流程

2.2　卡爾曼濾波算法

鐵路軌道線路是直線或平滑的曲線，當2個定位點距離較近時，即使在曲線地段也可以將鐵路軌道近似為1條直線。例如，普速鐵路區間困難地段的最小曲線半徑為500 m，利用直線近似軌道曲線的原理，列車從Vk-1定位點運行至Vk定位點，運行距離約10 m時產生的最大誤差為0.025 m；列車從Vk-1定位點運行至Vk+1定位點，運行距離約20 m時產生的最大誤差為0.100 m，如圖2所示。可見，直線、緩和曲線及曲線區段[4]均可由相鄰的定位點預測下一個定位點的位置。因此，采用卡爾曼濾波算法，建立基于軌道幾何特征的卡爾曼預測方程[5]，對采集的軌道定位數據中的野值數據進行判斷和剔除[6]。

圖2　曲線段近似為直線段的示意圖(單位：m)

假設列車當前的定位點為Vk，根據系統的模型，可以基于上一定位點Vk-1的位置預測定位點Vk的位置，即

X(k|k-1)=AX(k-1|k-1)+B

(1)

式中：X(k|k-1)為先驗估計值， 表示定位點Vk的位置預測值；X(k-1|k-1)為后驗估計值， 表示定位點Vk-1的位置最優值；A和B為由定位點Vk-1和Vk-2的位置最優值獲得的線性方程的參數。

用P表示協方差， 則X(k|k-1)的協方差可以表示為

P(k|k-1)=AP(k-1|k-1)AT+Q

(2)

式中：P(k-1|k-1)為X(k-1|k-1)對應的協方差；Q為經驗值，表示過程噪聲的方差，本文取Q=0.1。

令Z(k)為利用GNSS系統采集的實際測量值，再結合系統預測值即可得到定位點Vk的位置最優估計值X(k|k)為

X(k|k)=X(k|k-1)+Kg(k)(Z(k)-X(k|k-1))

(3)

其中

(4)

式中：Kg(k)為卡爾曼增益；R為經驗值，表示測量噪聲的方差，本文取R=0.1。

更新X(k|k)對應的協方差為

P(k|k)=(1-Kg(k))P(k|k-1)

(5)

根據以上卡爾曼濾波算法，運用式(1)可以由上一定位點Vk-1的位置估算出當前定位點Vk的位置，結合當前定位點Vk位置的實際測量值Z(k)，再運用式(3)可得到當前定位點Vk位置的最優估值X(k|k)。當實際測量值Z(k)偏差很大，即為野值時，通過最優估值X(k|k)可以修正偏差，剔除野值Z(k)。對式(1)—式(5)編寫計算機程序，通過程序的自回歸運算可以實現對整條線路軌道定位點中野值的剔除。

2.3　軌跡擬合

根據測量值誤差的算術平均值隨著測量次數的增加而趨于零的抵償性規律，對同一軌道線路進行多次測量，對每次測量的信息通過卡爾曼濾波算法剔除野值，采用算術平均的方法對多次生成的軌道曲線進行擬合，最終生成1條軌道擬合曲線，如圖3所示。軌跡擬合步驟如下。

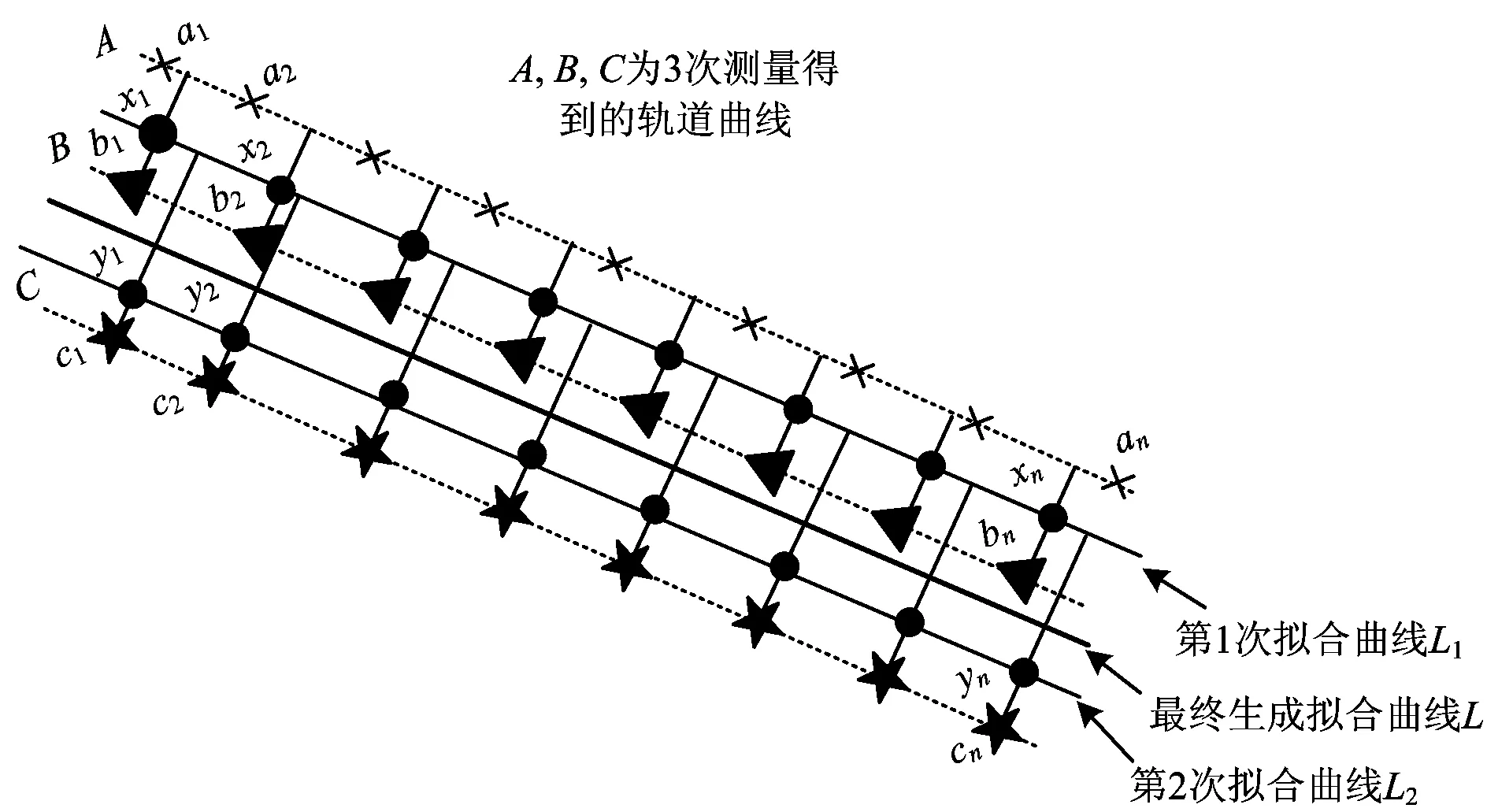
圖3　軌跡擬合示意圖

第1步：將定位點在WGS-84坐標系的坐標轉換為平面直角坐標系的坐標。

第2步：選擇曲線A作為基準曲線，選擇1條曲線B作為被擬合的曲線。

第3步：選取B中的1個定位點b1，在曲線A中有距離點b1最近的2個點a1和a2，由b1點向由a1和a2點構成的直線作垂線，取垂線段的中點x1作為新生成的曲線的點；以此類推，得到x1，x2，…，xn點，連接x1，x2，…，xn點，得到擬合曲線L1。

第4步：將L1作為基準曲線，再選擇1條曲線C作為被擬合的曲線，重復執行過程3得到擬合曲線L2。

第5步：再將L2作為基準曲線，…，以此類推，直到完成對全部曲線的擬合，最終得到1條軌道擬合曲線L。

第6步：將得到的軌道擬合曲線L由平面直角坐標系轉換為WGS-84坐標系。

2.4　數據約簡

為了去除冗余數據，采用垂直距離判據數據約簡算法[7]進行數據約簡。垂直距離判據數據約簡算法的原理為：設定垂距判定的閾值，判斷由當前定位點到前、后定位點連線的垂直距離是否不小于閾值，若不小于則保留當前定位點，否則此定位點為冗余點，可以刪去，從而實現數據約簡。

圖4　從當前定位點到前后定位點連線的垂直距離的示意圖

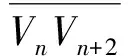
(6)

3　試驗驗證與分析

為了驗證提出的軌道電子地圖數據處理方法的合理性和有效性，在漢宜鐵路進行了現場試驗。在試驗動車組運行過程中，安裝在動車組上的GNSS車載設備多次采集軌道定位數據，根據本文所述算法編制了軌道電子地圖的數據處理及生成軟件，對采集的原始數據進行卡爾曼濾波、軌跡擬合、數據約簡等處理，最后生成了軌道電子地圖。

1)卡爾曼濾波

為了比較濾波的效果，采用原始數據和濾波后的數據分別生成軌道電子地圖，并展示在同一張地圖中，如圖5所示，對于明顯偏離的野值，通過濾波可以得到更為平滑的軌道曲線。

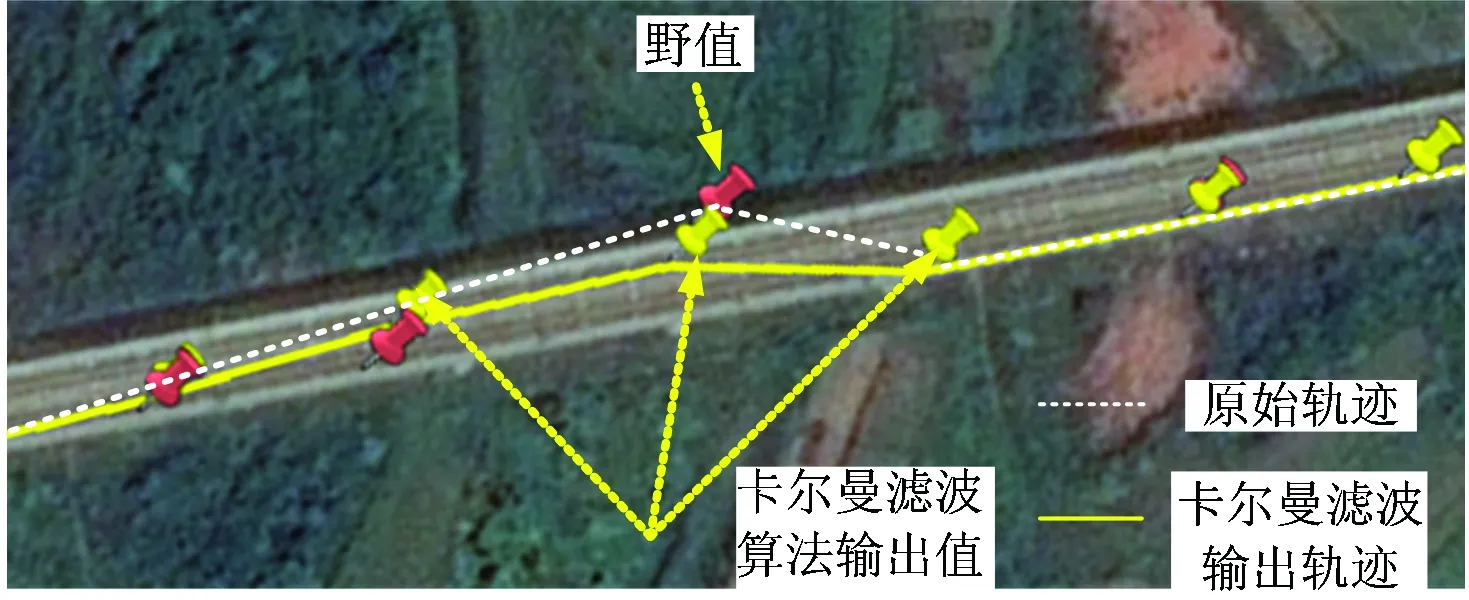
圖5　卡爾曼濾波效果圖

2)軌跡擬合

對由5次采集到的數據所生成的軌道曲線進行擬合，生成的軌道擬合曲線如圖6所示，從圖6可以看出，擬合曲線比較平滑。

圖6　軌跡擬合效果圖

3)數據約簡

漢宜鐵路全長約290 km，采集得到的軌道定位數據經卡爾曼濾波、軌跡擬合處理后共有定位點21 249個，采用垂直距離判據數據約簡方法對軌道擬合曲線進行數據約簡，約簡后定位點僅有5 408個，約為原來的25%，即約簡了75%，方便了數據的存儲和檢索。

4)軌道電子地圖的生成及定位精度驗證

采用處理得到的數據，運用地理信息系統技術生成目標軌道電子地圖，如圖7所示。

任意選取其中2次采集的軌道定位數據作為判定數據，針對判定數據中的每個定位點，均計算其到目標軌道電子地圖的距離，得到軌道電子地圖定

位匹配結果，如圖8所示。從定位匹配結果可知：判定數據中的定位點到目標軌道電子地圖的平均距離約為0.295 m，95%概率下距離約為0.705 m。由此可見，采用本文提出的數據處理方法生成的漢宜鐵路軌道電子地圖，定位精度較高，一致性較好。

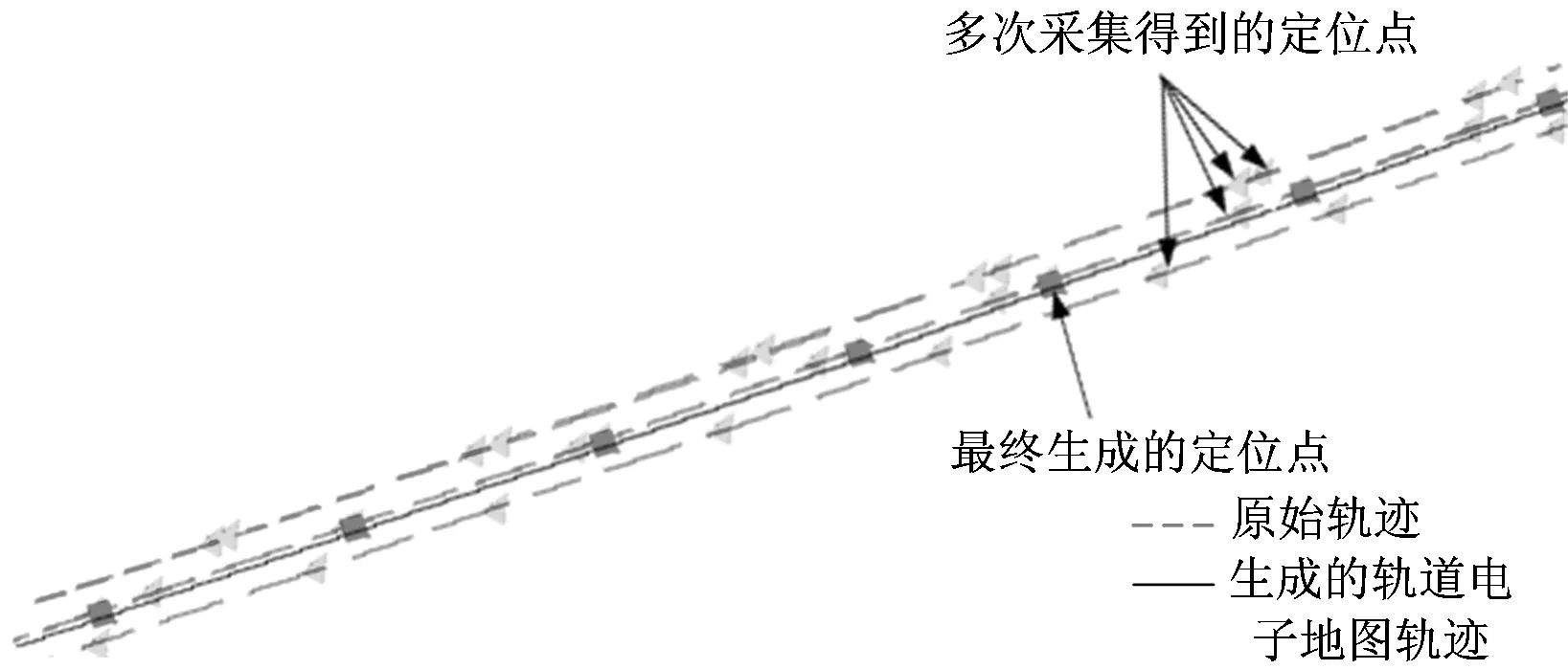
圖7　漢宜鐵路軌道電子地圖生成示例

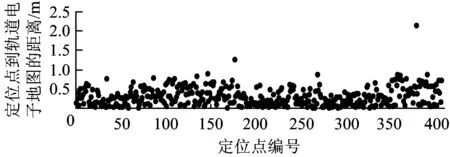
圖8　漢宜鐵路軌道電子地圖定位匹配結果

4　結　論

本文提出1種生成高精度軌道電子地圖的數據處理方法。該方法針對GNSS車載設備采集的軌道定位數據，分別采用卡爾曼濾波和軌跡擬合算法，有效地提高軌道電子地圖的精度；通過對直線區段和緩和曲線段定位數據的約簡，進一步提高了數據存儲和檢索效率。現場實測數據驗證結果表明，采用本文方法生成的軌道電子地圖定位精度高、一致性好，數據存儲和檢索方便，具有一定的應用價值。

[1]ROBERT Libbrecht,HELGE Sturesson.Low Cost Satellite Based Train Location System for Signalliog and Train Protection for Low-Density Traffic Railway Lines[R].Brussels:Information Society Technology,2005：1-74.

[2]K Tysen Mueller. Low-Cost, Precise Railroad GPS Vehicle Location System[R]. Washington D C: The Transportation Research Board of the National Academies, 2006.

[3]王莉.衛星導航系統定位精度估計[J].國防科技大學學報,2008,30(1):25-27.

(WANG Li.Estimation Positioning Accuracy of Satellite Navigation System[J].Journal of National University of Defense Technology, 2008,30(1):25-27. in Chinese)

[4]中華人民共和國鐵道部. TB 10621—2009 高速鐵路設計規范(試行)[S].北京:中國鐵道出版社,2010.

(Ministry of Railways of the People’s Republic of China. TB 10621—2009 Code for Design of High Speed Railway[S]. Beijing: China Railway Publishing House,2010. in Chinese)

[5]劉江,蔡伯根,唐濤,等.基于GPS的列控軌道地圖數據生成方法研究[J].測繪學報,2011,40(1):111-117.

(LIU Jiang,CAI Baigen,TANG Tao, et al.Research on GPS Based Track Map Data Generation Method for Train Control[J].Acta Geodaetica et Cartographica Sinica, 2011,40(1):111-117. in Chinese)

[6]王光鼎,張升康,楊汝良.一種基于卡爾曼濾波處理的北斗衛星無源組合導航自適應野值剔除方法[J].電子與信息學報,2008,30(8):1981-1984.

(WANG Guangding,ZHANG Shengkang,YANG Ruliang.An Adaptive Outlier Algorithm Based on Kalman Filtering for Beidou Satellite Passive Combination Navigation[J].Journal of Electronics & Information Technology, 2008,30(8):1981-1984.in Chinese)

[7]陳德旺,蔡伯根,王劍,等. 軌道交通GPS數據約簡的數學模型與算法研究[J]. 鐵道學報, 2008, 30(4):116-119.

(CHEN Dewang,CAI Baigen,WANG Jian,et al. Mathematical Model and Algorithm of Data Reduction for Railway GPS Data[J].Journal of the China Railway Society, 2008, 30(4):116-119. in Chinese)

[8]王劍. 基于GNSS的列車定位方法研究[D].北京:北京交通大學,2007.

(WANG Jian. Research of the Train Positioning Technologies Based on GNSS Technology[D].Beijing: Beijing Jiaotong University, 2007. in Chinese)

[9]SCHNEIDER U, TROELSEN J. Introducing Digital Map Information into Train Positioning Systems: Chances and Risks[C]//Seventh International Conference on Computers in Railway. Italy:WIT Press, 2000:1271-1280.