總體最小二乘法在相機標定中的應用

陸　玨

(上海市房地產科學研究院,上海 200031)

?

總體最小二乘法在相機標定中的應用

陸玨

(上海市房地產科學研究院,上海 200031)

摘要：對比總體最小二乘方法與最小二乘方法在相機標定中的適用性及優越性。在相機標定中，由于像點坐標和對應的地面點坐標均存在誤差，因此采用總體最小二乘方法對誤差方程中的系數矩陣及觀測向量同時改正，能夠建立更加合理的計算模型。文中以相機標定兩步法為例，通過實例解算，證明利用總體最小二乘法能夠得到精度更高的相機標定參數解。

關鍵詞：相機標定；最小二乘；總體最小二乘；兩步法；像差模型

非量測型相機不能提供準確的內方位元素和鏡頭畸變參數。為建立像點和對應物點的精確位置關系，需要進行相機標定[1]。當有多余觀測存在時，為得到參數的最佳估值，通常采用最小二乘(Least Squares,LS)方法進行求解。LS方法假設系數矩陣A沒有誤差，隨機誤差僅存在于觀測向量b中[2]。在多數相機標定的觀測方程中，b和A均包含了觀測值，即像點坐標和地面點坐標，這些點坐標均存在誤差。為了同時考慮觀測向量和系數矩陣的誤差，采用總體最小二乘(Total Least Squares,TLS)方法。TLS方法于1980年引入[2]，用于解決變量中的誤差(Error-In-Variables，EIV)模型的估計問題。近年來，Schaffrin對加權TLS進行研究[3]；陳義等研究穩健TLS的解法[4]；袁豹等討論總體最小二乘方法在線性回歸模型中的改正能力和優越性[5]，以及基于總體最小二乘的改進GM(1,1)模型在建筑物沉降中的應用[6]。

Tsai“兩步法”計算量適中、精度較高，因此在相機標定中最為常用。兩步法先用徑向排列約束得到部分外部參數的精確解，然后再將其余外部參數與徑向畸變系數進行迭代求解[7]。經典的兩步法對相機模型進行簡化，不能直接求出相機的像主點坐標[8-12]，且在建立像差模型時僅考慮鏡頭的徑向畸變。為了提高相機標定的精度，本文在兩步法解算中采用更為嚴密的相機成像模型。

本文以兩步法為例，將TLS方法引入相機標定解算中。通過實例的演算和比較，證明相對于LS方法，利用TLS方法能夠得到精度更高的相機標定參數。

1兩步法相機標定

兩步法的相機模型是一階徑向畸變的針孔模型。標定過程分兩步實現[7]：

第一步，求解三維物方坐標系到相應像平面坐標系的旋轉矩陣R和平移矩陣T中的Tx、Ty分量，以及圖像尺度因子Sx：

(1)

式中：(xw,yw,zw)為標定點在物方坐標系下的坐標；(Xd,Yd)為對應的像點坐標；f為有效焦距，r1~r9為旋轉矩陣R中的9個元素；Tx，Ty，Tz為平移矩陣T沿三維物方坐標系X，Y，Z3個軸的分量。若假定像主點與像平面中心重合，則內方位元素(x0,y0)為零。根據徑向約束條件，式(1)可以寫為

(2)

移項整理，并加入圖像的尺度因子Sx，可得觀測方程A1ξ1=b1：

(3)

參數m1=7，當每張像片上有n1≥7個對應點，即可解算出ξ1。根據R的正交性以及參數間的關系，可求出R和T中的Tx、Ty分量，以及圖像尺度因子Sx。

第二步，求解有效焦距f，平移矩陣T的Tz分量和透鏡的徑向畸變系數k。首先，不考慮畸變，建

立以f和Tz為未知參數的觀測方程A2ξ2=b2：

(4)

參數個數m2=2，當每張像片上有n2≥2個對應點，即可解出f和Tz的初值。接著，通過優化搜索計算f,Tz和k的精確值[7]。

經典兩步法追求解算的效率以及穩定性，同時考慮到計算機視覺中對相機標定的精度相對于攝影測量中要求較低而對嚴密相機模型進行簡化，不能直接求出相機的像主點坐標。為提高精度，本文對像主點坐標(x0,y0)進行標定，此時像點坐標記：x=Xd-x0，y=Yd-y0。同時，建立更為全面的像差修正模型。令徑向畸變系數為k1，偏心畸變徑向分量的畸變系數為p1，p2，薄棱鏡畸變徑向分量的畸變系數為s1，s2，則總像差模型為[13]

(5)

(6)

其中，g1=s1+p1，g2=s2+p2，g3=2p1，g4=2p2。包含像差和像主點坐標的非線性方程組：

(7)

(8)

R的9個元素中僅有3個獨立參數，因此需要利用R的正交性(RRT=RTR=I)建立6個條件方程：

(9)

對式(9)建立的條件方程賦予適當權值，聯合式(8)，采用加權平差方法進行解算。獨立參數個數m3=20-6=14，因此每張像片上需要有n3≥7個對應點。首先利用A1ξ1=b1和A2ξ2=b2計算部分參數的初值，再帶入A3ξ3=b3中計算所有未知參數的平差值。

2TLS在兩步法相機標定中的應用

在相機標定的觀測方程Aiξi=bi(i=1,2,3)中，bi和Ai均存在誤差。此時，采用TLS方法更為合理。TLS方法建立的變量中的誤差(EIV)模型中，觀測方程被定義為[2]

(10)

b∈Rn×1，ξ∈Rm×1，A∈Rn×m，且n>m=rank(A)。eb和EA分別代表了存在于觀測向量b和系數矩陣A中的隨機誤差(在LS中EA≡0)，eb和EA符合：

(11)

(12)

Q0∈Rm×m，QE∈Rn×n，?代表的是矩陣之間的直積：M?N:=[mij·N]，M=[mij]。目標函數為：

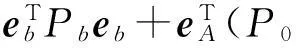
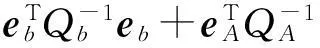
(13)

根據拉格朗日極值條件，建立方程：

(14)

λ為拉格朗日乘算子，(ξT?In)·eA=EA·ξ。在拉格朗日條件方程的基礎上，對方程中每個參數求導解算，解算過程為[3]：

第一步，解算初值：

(15)

第二步，迭代解算：

(16)

(17)

(18)

(19)

式(19)計算的單位權方差有偏，偏差可通過數值計算的方法得到[14]。由于偏差較小，對本文的結果沒有影響。在計算中若出現法方程病態的情況，則采用Tikhonov正則化方法解算。

相機標定結果的精度可以采用畸變圖像誤差進行評定[8-12]，也可利用多張像片空間前方交會計算特征點的世界坐標，與已知的物方點三維坐標進行比較。

3實例分析

本例通過兩步法對相機進行標定。標定點共38個，分布在建筑的兩面墻及三級臺階上。標定點的物方坐標用測角精度1″，測距精度0.6 mm+2 ppm的索佳NET1200全站儀測定，測量距離在100 m以內，每個點測量4次，因此控制點的精度mm。

相機為Nikon D200，像幅23.6 mm×15.8 mm (3 872×2 592像素)，焦距初值8 500像素。實驗共進行3次，每相鄰兩次拍攝的時間間隔為一周，每次拍攝共設8個攝站，每站拍攝1張像片，每次檢校都利用當次所拍攝的8張像片進行聯合解算，如圖1所示，攝影距離為15~20 m。

利用更為嚴密的兩步法對相機進行標定。在平差中，分別用LS方法和TLS方法進行計算。結果如表1和表2所示。

表1　兩步法相機標定結果

圖1　第一次相機標定像片

次數計算方法畸變圖像誤差多片前交結果與已知值之差的中誤差中誤差/像素最大值/像素最小值/像素X方向/mmY方向/mmZ方向/mm點位中誤差/mm1LS0.12694.14940.02191.40741.20090.36601.8860TLS0.07751.05940.02020.77270.38170.15320.87532LS0.05921.37140.03681.70870.67850.24341.8545TLS0.05501.32520.03120.67470.39110.10240.78653LS0.14702.63140.10481.06870.56330.26031.2358TLS0.11672.53380.09180.64710.41890.23140.8048

由表1的結果可以看到，無論是利用LS方法還是TLS方法，標定的相機內參數結果均比較穩定。在表2中，TLS方法計算的畸變圖像誤差小于LS的計算結果；且利用TLS計算的兩步法點位偏差中誤差均在1 mm之內，而LS的計算結果則大于1 mm。因此，TLS方法計算得到的結果精度高于LS方法。

4結論

本文將TLS方法引入相機標定解算中，并以兩步法為例，對算法進行驗證，得到結論：

1)在相機標定的誤差方程中，系數矩陣和觀測向量均包含觀測值。由于TLS方法建立的EIV模型對所有變量中的誤差都進行最小化的約束，與系數矩陣完全準確的LS方法相比，TLS方法更適用于相機標定的解算。

2)利用TLS方法計算的兩步法相機標定結果，無論是畸變圖像誤差還是多片前交結果與已知值之差，均小于LS方法的計算結果，即TLS計算的相機標定參數精度高于LS的標定結果。

3)采用更加嚴密的兩步法進行相機標定，在未知相機像面中心預標定值的情況下，通過計算可以直接得到相機像主點坐標，并且像差模型也更加完整。

參考文獻：

[1]張廣軍.視覺測量[M].北京：科學出版社,2008:102-110.

[2]GOLUB H G,VAN LOAN F C.An Analysis of the Total Least Squares Problem[J].SIAM Journal on Numerical Analysis,1980,17(6)：883-893.

[3]SCHAFFRIN B,WIESER A.On Weighted Total Least-Squares Adjustment for Linear Regression[J].J Geodesy,2008,82:415-421.

[4]陳義,陸玨.以三維坐標轉換為例解算穩健總體最小二乘方法[J].測繪學報,2012,41(5)：715-722.

[5]袁豹,岳東杰.關于總體最小二乘方法適應性實驗研究[J].測繪工程,2012,21(6)：22-26.

[6]袁豹,岳東杰,李成仁.基于總體最小二乘的改進GM(1,1)模型及其在建筑物沉降預測中的應用[J].測繪工程,2013,22(3)：52-55.

[7]ROGER Y,TSAI.A Versatile Camera Calibration Technique for High-Accuracy 3D Machine Vision Metrology Using Off-The-Shelf TV Camera and Lenses[J].IEEE Journal of Robotics and Automation,1987,RA-3(4)：323-344.

[8]張學民,宋述穩.兩步法攝像機標定的改進[J].自動測量與控制,2006,25(9)：73-75.

[9]曹良中，楊遼，闞培濤，等.地面檢校場的非量測型數碼相機檢校[J].測繪科學，2015，40(2)：132-137.

[10] 張陽陽，門林杰，周桂初，等.數字相機在類似棋盤檢校場中的檢校方法研究[J].測繪工程，2015,24(2)：55-59.

[11] 張春森，馮鵬飛.相機檢校控制場像點坐標自動定位與高精度量測[J].測繪科學，2015，40(3)：76-79.

[12] 趙海強，李浩，錢海明，等.多相機數碼影像光束法解算及精度分析[J].測繪工程，2015,24(4)：28-32.

[13] WENG J,COHEN P,HERNIOU M.Camera Calibration with Distortion Models and Accuracy Evaluation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(10)：965-980.

[14] SHEN Y Z,LI B F,CHEN Y.An Iterative Solution of Weighted Total Least-Squares Adjustment[J].J.Geod.,2011,85：229-238.

[責任編輯：李銘娜]

On total least squares for camera calibration

LU Jue

(Shanghai Real Estate Science Research Institute,Shanghai 200031,China)

Abstract：The applicability and superiority of Total Least Squares (TLS) and Least Squares (LS) in camera calibration have been studied in this paper.Because the coordinates of the ground point and the image point all exist errors,the total least squares solution is preferably used here,for that the errors exist both in the observation vector and the coefficient matrix.The example of two-step camera calibration is carried out to demonstrate the performance of the TLS method.The result shows that camera calibration parameters calculated through the TLS method is more accurate.

Key words：camera calibration；least squares；total least squares；two-step method；distortion model

中圖分類號：P231

文獻標識碼：A

文章編號：1006-7949(2016)03-0006-05

作者簡介：陸玨(1985-)，女，博士，工程師.

基金項目：上海市住房保障和房屋管理局基金資助項目(2014-03)

收稿日期：2014-06-13