考慮公交車流運行速度的城市短時交通流預測方法研究

2016-04-20 10:41:25潘紅范宏建

公路與汽運 2016年2期

潘紅,范宏建

(1.上海市長寧區交通管理中心,上海 200050;2.上海力陽道路加固科技股份有限公司,上海 201599)

潘紅1,范宏建2

(1.上海市長寧區交通管理中心,上海 200050;2.上海力陽道路加固科技股份有限公司,上海 201599)

摘要:目前,短時交通流預測已成為城市智能交通發展中的一個瓶頸。文中通過對具有固定時域與周期性運行的公交車流速度的數據分析,發現公交車流運行速度與本時域內的短時交通流具有較好的相關性,對本時域內的短時交通流的運行特征會產生特定的標記作用,進而運用BP人工神經網絡方法,利用公交車流運行速度來預測城市短時交通流,并將預測結果與常規城市短時交通流BP人工神經網絡預測結果進行對比,驗證了該方法良好的預測效果。

關鍵詞:城市交通;智能交通(ITS);短時交通流預測;公交車流;BP人工神經網絡

隨著中國快速城市化,與日俱增的機動車給城市交通帶來巨大壓力,交通問題日益突顯。智能交通ITS是有效解決城市交通問題的關鍵途徑,其實施的一個重要環節是短時交通流的科學預測。由于短時交通流變化過程的隨機性、不確定性,隨著統計時間的變短,交通流變化的不確定性越來越顯著。同時,城市短時交通流變化的不確定性還與上下游的交通流、天氣變化、交通事故和交通環境等因素相關聯。如何在具有不確定性的交通流變化過程中對城市短時交通流進行科學、準確、系統的數據分析,找出其中的規律,建立相應的預測方法和模型是需要解決的問題。在不考慮私有汽車、出租車及行人參與的混合交通流條件下,城市路網中通行的公交車流作為整個交通流的一部分,由于公交車的運行路線固定,發車規律,公交車流在道路上的運行狀態變化相對具有周期性與規律性。因此,該文運用BP人工神經網絡方法,對考慮公交車流運行速度的城市短時交通流預測方法進行研究。

1 原理分析

城市短時交通流預測是城市交通控制和交通誘導的一項基礎性工作。對于城市交通控制和交通誘導而言,誘導周期一般不超過5 min,控制周期一般為2～5 min,因而要求城市短時交通流預測的時間短。一般把短于15 min的城市交通流預測稱為城市短時交通流預測,其預測內容一般為交通量、平均速度、平均密度(或占有率)和旅行時間等。現有城市交通流短時預測的原理如下:已知i路段及i+j路段在過去p個時刻的交通流參數值vi+j(t-k)(k=1,2,…,p),求出第i路段未來k個時段內交通流狀態估計值vi(t-k),其中vi+j(t-k)稱為預測因子,包括時間數據和空間數據。時間數據主要是指i路段過去若干時刻間隔交通流參數及歷史平均值;空間數據是指與i路段相鄰上下游路段i+j當前和過去各時刻交通流參數。

通過采集某路口一天幾個主要時刻t公交車流的運行速度與對應本路口10 min后即t+10 min的交通流運行速度,畫出兩個對應曲線的趨勢變化進行對比研究(如圖1所示)。

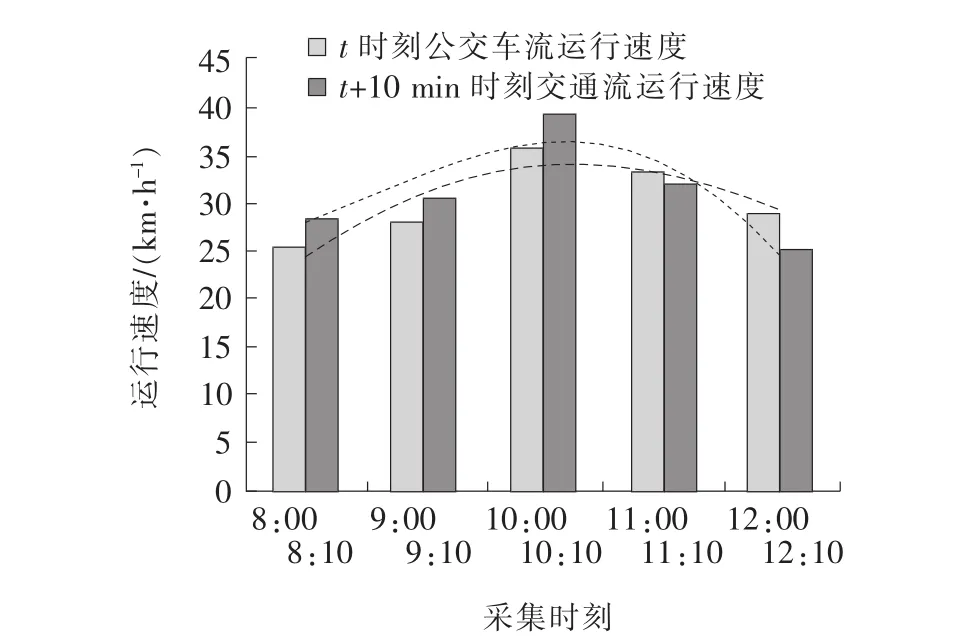
圖1 公交車流運行速度變化趨勢

由圖1可見:在本路口隨著不同t時刻公交車流運行速度的增大,t+10 min的交通流運行速度也呈增大趨勢;同時,隨著不同t時刻公交車流運行速度的減小,t+10 min的交通流運行速度也減小。說明在短時間間隔內,公交車流的運行速度與10 min的交通流運行速度的變化趨勢具有較好的相關性,這是因為相對于普通車流運行速度,以t時刻公交車流運行速度作為預測因子的變化趨勢更具有規律性與固定性。

2 數據采集

目前國內研究多集中于有時間因子影響的單點或單步預測模型,其中單點模型只考慮預測點自身歷史數據,不考慮其他路段和交叉口;單步預測模型指t時刻只預測緊鄰時刻t+l的交通流參數,以此類推滾動預測,在該文中即只采集預測單路口t時刻公交車流的運行速度。為此,只考慮i路段t時刻的公交車輛運行速度vi(t)作為預測因子,預測緊鄰時刻t+l的交通流參數,并通過線圈檢測器、微波檢測器、紅外檢測器、視頻檢測器等常用檢測設備對預測路口公交車流運行速度進行采集。數據采集內容包括信息ID、車牌號、數據上報時刻、所在經度、所在緯度、標記車流流向。

3 方法建模

早中期城市短時交通流預測多以回歸分析和時間序列預測為主,由于主要以線性分析為基礎,其無法及時反映城市交通系統中不確定與非線性狀態,因而預測精度不理想。現在一些適應能力強、計算效果好、抗干擾能力強的理論方法被應用到城市短時交通流預測中,人工神經網絡模型就是其中之一,因其具有實時信息更新網絡、保證預測實時性的特點,與傳統方法相比較,其能更有效地解決城市短時交通流預測方面的問題。

BP人工神經網絡是目前應用最廣泛的一種人工神經網絡,它是一種多層前饋網絡,包含輸入層、隱含層和輸出層,同層單元之間不相連,是一種單向傳播、具有從輸入到輸出的高度非線性映射的多層前向網絡。在輸入層和輸出層之間可有一個或多個隱含層,由信息的正向傳播和誤差的反向傳播兩個過程組成,信號向前逐層傳遞,不帶反饋和層內相互連接結構,上層節點輸出值只會影響下層節點的輸入值;通過參數調整即誤差反向傳播過程調整網絡的連接權值,在最小均方差條件下使網絡輸出值最大程度地接近于期望輸出值。其網絡結構如圖2所示。下面運用BP人工神經網絡方法,考慮公交車流運行速度來預測城市短時交通流。

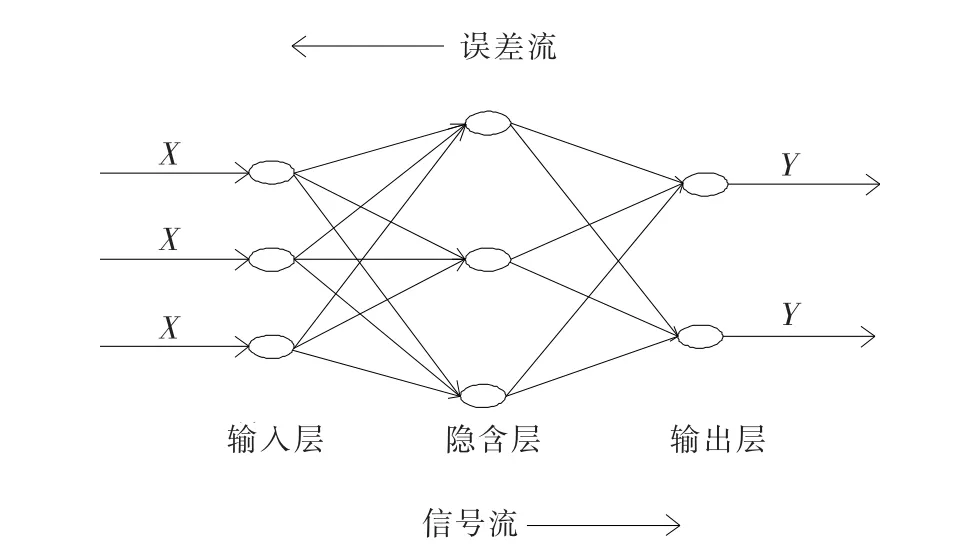
圖2 BP人工神經網絡的結構

3.1 建模原則

基于BP人工神經網絡的短時交通流預測模型的建立原則如下:

(1)精確性,即預測結果滿足精度要求。

(2)實時性,表現為計算的復雜性,要求能在規定的時間內求出結果,及時獲取交通流信息。

(3)動態反饋性,要求在發生異常情況時,能根據實際情況動態反饋,進行調整。

(4)可移植性,即模型能通過參數調整而具有時空移植性。

3.2 神經元函數

在人工神經網絡中,在生物神經中神經元和突觸是神經網絡的基本組成部分,神經元常被稱為處理單元或節點。人工神經元的假定,是對生物神經元進行簡化和概括,更便于數學化表達。圖3為人工神經元結構模型。

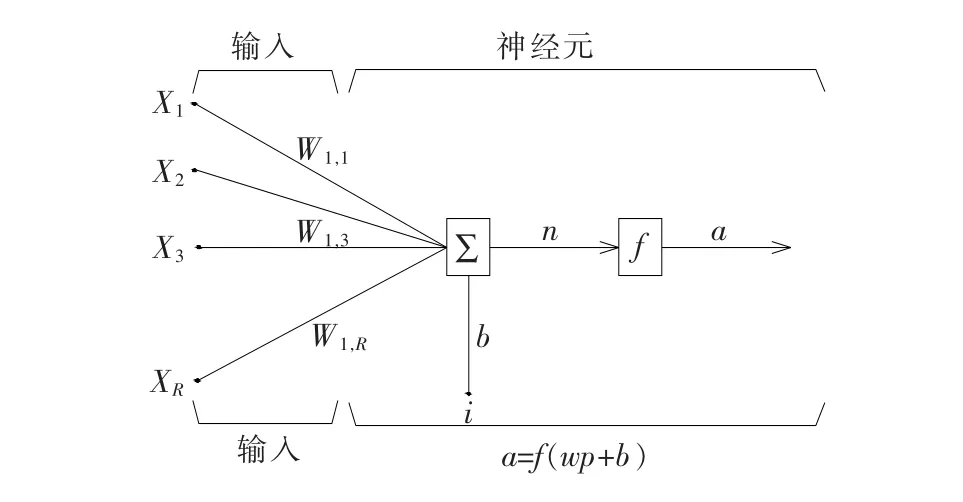
圖3 人工神經元模型圖

根據不同的人工神經元輸入、輸出特性,可采用不同的傳遞函數。sigmoid函數在同一網絡中既能處理小信號,也能處理大信號,該函數中區的高增益解決了小信號需要放大的要求,而兩側的低增益適宜處理大的凈輸入信號。鑒于此,模型網絡的隱含層神經元的轉移函數采用sigmoid函數中取值范圍為(0,1)的非線性的單極性對數函數Iogsig(S型函

數),其表達式如下:

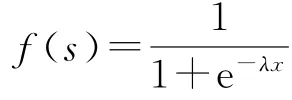
式中:λ為S型函數的壓縮系數,這里令其為1,即

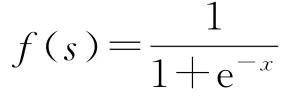
由于模型輸出層為單一的交叉口交通流量值,為了在輸出得到具體數值,輸出神經元轉移函數采用線性函數purelin。

3.3 模型結構

模型中,取輸入數據的維數為1,用一個一維的向量X表示;輸出數據的維數為1,用一個一維的向量Y表示,即X=vi(t),Y=vi(t+1)。網絡輸入層、輸出層的節點數均為1。

BP人工神經網絡的隱含層數量和隱含層節點數的設計,從結構上決定著網絡性能的優劣,它是模型建立成敗的關鍵。隱含層一般為1～2層,該模型采用1層隱含層。對于BP人工網絡的隱含層神經元數,首先根據輸入節點數2n+1的經驗方法來確定,該網絡模型中的輸入層節點為1個,暫定隱含層神經元數為3個;再通過數據樣本,基于MATLAB人工神經網絡工具箱的訓練試驗來修正網絡,訓練函數采用默認函數trainlm,訓練步長為10 000,精度值為0.000 01,學習率為0.01。通過逐步增加或減少隱含層神經元數來調整網絡,直到滿意精度。

3.4 模型測試

網絡模型經過MATLAB人工神經網絡工具箱訓練好后,輸入檢驗樣本,根據檢驗誤差測試網絡性能。利用仿真函數對訓練好的網絡進行檢驗,函數表達式如下:

a=sim(net,p)

式中:a為網絡輸出;net為網絡對象;p為輸入向量或矩陣。

若p為向量,則是單點仿真;若p為矩陣,則是多點仿真。最終確定BP人工神經網絡預測模型隱含層節點數取6,輸出層為1個節點,即網絡初始結構為1×6×1。

4 方法應用

依據上述數據采集方法,隨機對某一路口進行不同時刻實際數據采集,預測10 min后該路口的實際交通運動參量,即輸入層輸入采集樣本為t時刻該路口公交車流的運行速度,預測t+10 min時刻該路口交通流運行速度參量。同時,為對該預測方法進行對比評價,針對常規BP人工神經網預測方法進行數據采集,即輸入層輸入采集樣本為t時刻該路口普通車流的運行速度,預測t+10 min時刻該路口交通流運行速度參量。以均方誤差MSE作為模型預測性能的評價指標,對比結果如圖4和圖5所示。

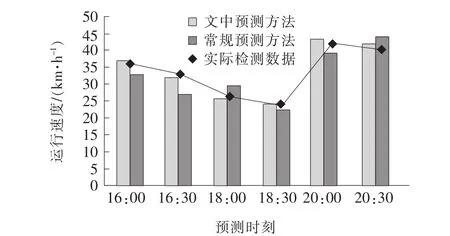
圖4 交通流量預測結果對比

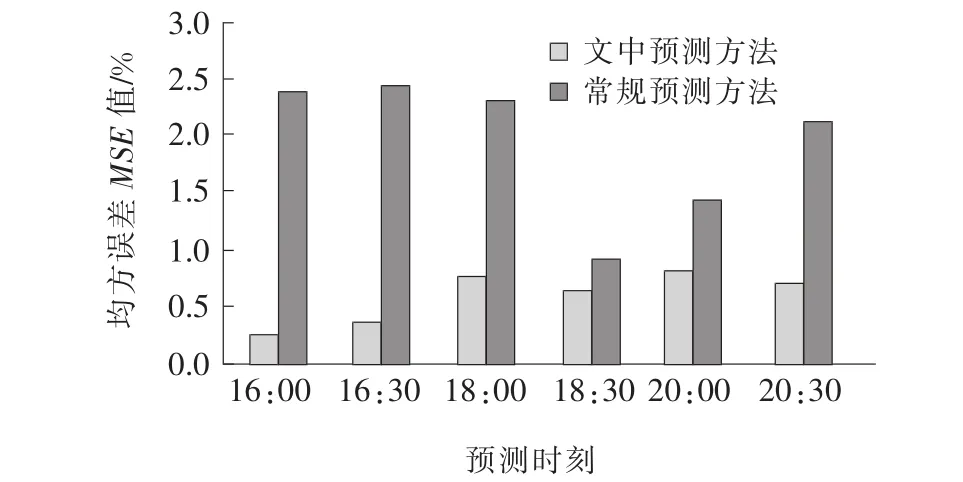
圖5 交通流量預測均方誤差MSE值對比

由圖4可見:相比于常規預測方法,運用文中方法得到的不同時刻的預測值都更接近于實際值,說明文中方法較好的預測效果不具有偶然性。這是由于相對于采用本身隨機性、不確定性的普通車流作為預測輸入樣本,采用線路固定、發車規律的公交車流作為預測輸入樣本具有周期性,其預測效果具有一定的可靠性。

由圖5可見:文中預測方法在不同時刻的預測均方誤差MSE值均在1%內,遠小于常規預測方法的均方誤差MSE值。說明文中方法的預測效果具有較好的穩定性。一般交通流量預測均方誤差MSE值要求為1%～10%,采用文中預測方法在滿足預測要求的前提下,可保證較好的精度,達到理想的預測效果。

5 結語

該文通過采集某路口一天幾個主要時刻公交車流的運行速度與短時間間隔內對應該路口的交通流運行速度,發現公交車流的運行速度與下一時刻的交通流運行速度的變化趨勢具有較好的相關性。運用BP人工神經網絡方法,考慮公交車流運行速度來預測城市短時交通流,與常規預測方法相比,該方法在不同時刻的預測值都更接近于實際值,說明該預測方法較好的預測效果不具有偶然性,保障了預測方法應用的可靠性與穩定性,同時該預測方法在滿足預測要求的前提下可保證較好的精度,達到理想的預測要求,具有較高應用價值。

參考文獻:

[1]陸鍵,項喬君.智能運輸系統(ITS)規劃與應用[M].南京:江蘇科學技術出版社,2008.

[2]吳浩勇.城市快速路交通參數預測方法研究[D].長春:吉林大學,2005.

[3]李貞珍.神經網絡在城市交通流預測模型中的應用研究[D].上海:上海交通大學,2007.

[4]周剛.智能公交調度系統通信協議研究與實現[D].武漢:華中師范大學,2008.

[5]馬壽峰,賀國光,劉豹.智能交通系統中短時交通流預測系統的研究[J].預測,2004,23(2).

[6]秦偉剛.基于人工神經網絡的智能交通系統檢測與控制[D].濟南:山東大學,2005.

[7]戴娟莉,宋奇文.基于多因素的交通指數回歸分析短時預測研究[J].公路與汽運,2015(3).

[8]范騰騰.城市道路交通流量短時預測研究[D].北京:北京交通大學,2010.

[9]劉麗娜.城市道路交通流量短時預測的研究[D].北京:北京郵電大學,2010.

[10]夏冰,董菁,張佐.周相似特性下的交通流預測模型研究[J].公路交通科技,2003,20(2).

[11]蔡巖.基于灰色預測模型的短期交通流預測研究[D].成都:西南交通大學,2009.