并行FDTD方法在海面及其上方漂浮目標復合電磁散射中的應用

賈春剛　郭立新, 2　劉偉　尤立志

(1.西安電子科技大學物理與光電工程學院,西安 710071;2.西安電子科技大學 綜合業務網理論及

關鍵技術國家重點實驗室,西安 710071;3.中航工業雷達與電子設備研究院

航空電子系統射頻綜合仿真航空科技重點實驗室,無錫 214063)

?

并行FDTD方法在海面及其上方漂浮目標復合電磁散射中的應用

賈春剛1郭立新1, 2劉偉1尤立志3

(1.西安電子科技大學物理與光電工程學院,西安 710071;2.西安電子科技大學 綜合業務網理論及

關鍵技術國家重點實驗室,西安 710071;3.中航工業雷達與電子設備研究院

航空電子系統射頻綜合仿真航空科技重點實驗室,無錫 214063)

摘要利用基于圖形處理器(Graphics Processing Unit， GPU)的并行時域有限差分(Finite Difference Time Domain, FDTD)法計算一維粗糙海面及其上方二維漂浮目標的復合電磁散射.采用各向異性完全匹配層(Uniaxial Perfectly Matched Layer， UPML)吸收邊界作為截斷邊界,為了便于并行程序的設計,在整個計算區域使用UPML吸收邊界差分公式進行迭代.利用異步通信技術來隱藏主機和設備之間的通信時間,同時使用片上的共享存儲器提高讀取速度,進一步對程序進行優化,得到很好的加速比,證明了該方法的計算高效性.通過與串行FDTD法以及串行矩量法獲得的數值結果進行比較,驗證了該并行方法的正確性,進而研究了海面上方類似艦船漂浮目標的電磁散射特性,討論了入射角、海面風速以及目標吃水深度對雙站散射系數的影響.

關鍵詞復合散射;海面;漂浮目標;FDTD;GPU

DOI10.13443/j.cjors.2015010501

Application of parallel FDTD to EM scattering from a target floating on sea surface

JIA Chungang1GUO Lixin1,2LIU Wei1YOU Lizhi3

(1.SchoolofPhysicsandOptoelectronicEngineering,XidianUniversity,Xi’an710071,China;2.StateKeyLaboratoryofIntegratedServicesNetworks,XidianUniversity,Xi’an710071,China;3.AviationKeyLaboratoryofScienceandTechnologyonAISSSRadarandAvionicsInstituteofAVIC,Wuxi214063,China)

Abstract In this paper, GPU-based FDTD algorithm is applied to study the electromagnetic(EM) scattering from two-dimensional(2-D) target floating on one-dimensional(1-D) rough sea surface with Pierson-Moskowitz(PM) spectrum. The FDTD lattices are truncated by uniaxial perfectly matched layer (UPML), and the finite-difference equations are employed in the whole computation domain for the parallelization convenient to carry out. Also, the parallelism design is limited to the iteration of the near field that is extremely time consuming. To improve the performance, asynchronous transfers is implemented to mask the memory transfers time and the shared memory is used to achieve high memory bandwidth. Using compute unified device architecture(CUDA) technology, significant speedup ratios are achieved, which demonstrates the efficiency of GPU accelerated the FDTD method. The validation of our method is verified by comparing the numerical results with these obtained by sequential FDTD executing on CPU as well as method of moments (MOM), which shows favorable agreements. Furthermore, our parallel implementation is employed to study the influences of the incident angle, the wind speed, the depth of the target on the EM scattering from the target and a sea surface composite model.

Keywords composite scattering; sea surface; floating target; FDTD; GPU

引言

隨著雷達遙感和目標檢測技術的飛速發展,因其在海洋遙感、目標識別和雷達探測等軍事以及民用領域具有重要的應用價值[1-2].海面與目標復合電磁散射的研究越來越得到國內外學者的廣泛關注.目前為止,針對這種隨機問題的解決方法總結起來主要分為兩大類:高頻近似方法和數值算法.其中,以高頻方法為例:基爾霍夫近似[3]、小斜率近似[4]、微擾法[5]以及雙尺度[6]等,由于上述方法只限于單次散射,無法考慮多次散射與多徑傳播、邊緣衍射、相位干涉產生的Bragg諧振散射等復雜過程,用來解決單純粗糙面散射問題.對于粗糙面與目標復合散射,目標與粗糙面復雜的相互作用,因此數值方法廣泛地用于計算上述復合電磁散射模型,如矩量法[7]、快速多極子[8]、時域有限差分法(Finite Diffe-rence Time Domain, FDTD)方法[9]等.數值方法由于直接對Maxwell微分或積分方程進行數值求解,因而適用范圍廣,并且計算精確度高,但受計算機內存和時間的限制,計算效率不高.因此,針對數值方法的加速算法相繼被提出,如基于信息傳遞接口(Message Passing Interface，MPI) 的并行矩量法[10]、并行FDTD 法[11],有效地減少了計算時間.

然而,上述并行方法的加速比受限于計算機CPU核數,對計算機的硬件要求很高.近些年,基于GPU的統一計算設備架構(Compute Unified Device Architecture, CUDA)技術廣泛地用于電磁場的數值模擬中[12-13].與并行的CPU技術相比,GPU由于其強大的計算能力能夠輕松地實現很高的加速比.FDTD方法在求解粗糙面與目標復合散射問題時,有其自身的優點,由于采用統一剖分建模,電磁參數已經反映在每一個網格的電磁場計算中,因此它很容易處理復雜介質電磁散射模型.并且電場(磁場)分量的迭代公式只與它本身上一時刻的場值和周圍網格磁場(電場)上半個時間步的值有關,而與計算區域內其它場量沒有直接的關系,因此它具有天然的并行能力.基于GPU 的并行FDTD方法雖然已經應用于很多的電磁場數值模擬中,但在粗糙面電磁散射特性的研究中尚未涉及到.因此,本文首次提出利用FDTD方法結合GPU并行技術解決粗糙面與目標復合模型電磁散射問題.與傳統的FDTD方法相比,該方法在處理電大尺寸粗糙面與目標復合散射問題時具有明顯優勢.

本文采用FDTD方法結合基于GPU的并行技術討論了一維海面與上方漂浮類艦船目標的復合電磁散射特性.第二節介紹了海面的生成以及復合散射的FDTD方法計算模型,并且詳盡地描述了基于GPU的FDTD方法加速算法在解決粗糙面與目標復合散射時的并行以及優化方案;第三節從計算準確性和計算效率兩個方面驗證了本文基于GPU的FDTD方法解決粗糙面與目標復合散射問題的有效性,在此基礎上,進一步討論了入射角、海面風速以及目標吃水深度對海面與上方漂浮類艦船目標復合電磁散射特性的影響;最后,給出了相應的結論以及今后工作的研究重點.

1理論分析

1.1復合散射模型

圖1以TM入射波為例,給出了一維海面及其與上方二維漂浮類似艦船目標復合的電磁散射模型,入射波入射矢量ki,與y軸正方向夾角為入射角θi,ks為散射波矢量,與y軸正方向夾角為散射角θs,h為艦船目標的吃水深度,L為海面的模擬長度y=f(x)為海面輪廓,本文采用Pierson-Moskowitz (PM)譜來描述海面輪廓的起伏,功率密度函數為[14]

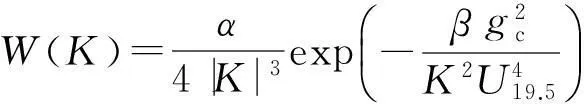
(1)

式中： 空間波數K=2π/L;U19.5為海面高度19.5 m處的風速；α=8.10×10-3以及β=0.74分別為經驗常數; 重力加速度常數gc=9.81 m/s2.圖1復合散射模型中,當入射波為平面波時,總場邊界需設置均勻的等效面電磁流,而總場邊界的左右兩端被吸收邊界截斷,導致等效面電磁流在左右兩端處有突變,為了克服這一缺點,本文引入了高斯窗函數[15]

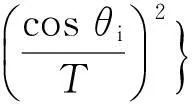
(2)

式中:xcen和ycen為連接邊界處的中心點坐標;T為常數,決定了高斯窗函數的寬度,當邊緣值為中心點處的10-3時,滿足關系cos(θi)/T=2.6/ρm,其中ρm為中心點到邊緣處的最小距離,對于一維粗糙面而言,與y方向上的的變化沒有關系,即y=ycen.

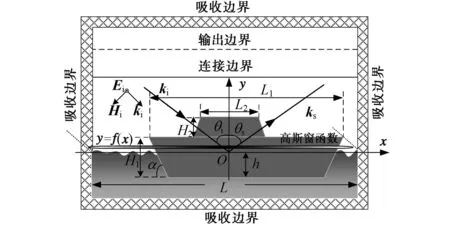
圖1　一維海面與艦船目標復合電磁散射模型

由于海面與目標的復合電磁散射屬于半空間問題,圖 1中,只在計算區域的上半部分加入了虛擬的外推邊界以及連接邊界.為了在有限的區域內模擬無限的空間電磁散射問題,在計算區域最外層的截斷邊界處加入吸收邊界,本文使用了各向異性完全匹配層吸收邊界[16],為了便于并行化設計,在整個計算區域使用吸收邊界的差分公式進行迭代;連接邊界[16]將計算區域劃分成總場區和入射場區,并應用惠更斯原理,在此邊界引入入射波;當近場迭代達到穩定之后,在外推邊界處的近場做近遠場變換實現遠場的外推[16],得到遠區散射場,進而獲得對粗糙面長度歸一化的雙站散射系數:

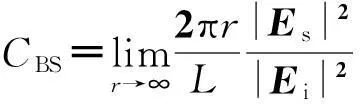
(3)

1.2FDTD方法計算海面與目標復合散射的GPU并行方案

該部分介紹了并行平臺以及CUDA編程模型.詳盡地闡述了基于GPU的FDTD方法計算粗糙面電磁散射的并行策略,在此基礎上,利用異步傳輸技術以及共享存儲器對其進一步優化,提高并行效率.

1.2.1CUDA編程模型

英偉達推出了CUDA編程模型的GPU顯卡之后,由于其相對簡單的并行化設計,憑借其強大的計算能力在各個領域到了廣泛的推廣和應用.串行程序在主機(CPU)上執行,具有高度并行化的數據則在設備上(GPU)進行處理.并行程序首先在主機上串行執行,包括CPU內存和GPU顯存的分配、初始化以及內存和顯存的釋放;在設備上由成千上萬線程并行執行的函數稱為核函數,不同核函數在主機上串行執行.在CUDA編程模型中,主機和設備上的存儲器在物理上是分離的.

1.2.2并行化設計

圖2所示為并行FDTD方法計算粗糙面電磁散射的并行化設計的流程圖.首先如前文所述,利用模特卡洛方法模擬PM海面的輪廓建立復合散射模型,然后CPU根據計算問題的未知量個數分配內存和顯存大小.FDTD方法計算時,在近場的迭代很耗時并且具有很好的并行特性,所以并行化處理在此處進行.由于整個網格線程間需要進行數據交換,所以需要重新調用一個核函數進行同步,但全局存儲器的讀寫速度很慢,所以應盡量使用少的核函數,本算法使用5個核函數來實現近場迭代功能,包括IncidentHKernel()(入射波磁場分量的更新)、IncidentEKernel()(入射波電場分量的更新)、ConnectionKernel()(連接邊界處引入入射波)、eKernel()(電場分量的更新)、hKernel()(磁場分量的更新).當GPU完成近場迭代時,遠區散射場很容易由CPU平臺得到.

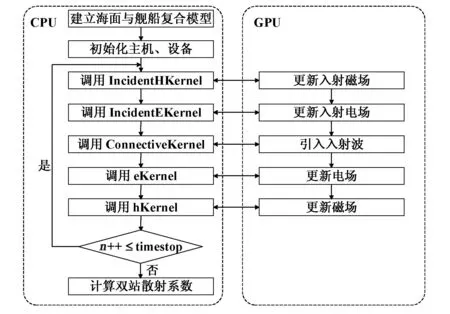
圖2　并行FDTD方法計算海面與目標復合散射流程圖

1.2.3并行優化方案

1) 共享存儲器

以TM入射波為例,在Ez(i,j)分量進行迭代時,需要前一時刻的Hy(i,j)和Hy(i-1,j)以及Hx(i,j)和Hx(i,j-1),而其相鄰的Ez(i-1,j)分量進行迭代時,需要前一時刻的Hy(i-1,j)和Hy(i-2,j)以及Hx(i-1,j)和Hx(i-1,j-1),所以可以看出在當前Ez分量進行迭代時,需要從全局存儲器中讀取兩次的前一時刻的Hx和Hy分量,由于在對全局存儲器讀寫時的訪問延遲很高,所以極大地影響了并行效率.因此,利用片上的共享存儲器提高讀取速度,只需要從全局存儲器中讀一次數據到共享存儲器中,然后數據就可以在共享存儲器中進行重復的讀取,大大降低了線程間的通信時間.當磁場分量Hx和Hy進行迭代時,不僅當前線程塊的電場的值Ez要從全局存儲器拷貝到共享存儲器里,而且其相鄰的右邊線程塊最左邊一列的值和相鄰的下邊線程塊最上面一行的值也要傳到共享存儲器;當電場分量進行迭代時,當前線程塊的磁場分量Hx的值,以及相鄰下邊線程塊的最上一行的值都要傳到共享存儲器.磁場分量Hy當前線程塊以及相鄰右邊線程塊最左邊一列的值都要傳到共享存儲器中.

2) 異步傳輸

主機與設備之間的數據交換非常耗時,尤其在計算電大尺寸問題時,主機與設備之間的數據交換量巨大,極大地影響了并行程序的計算效率.因此,本文利用CUDA模型中的異步功能來隱藏主機與設備之間的數據通信,即設備端的計算與主機與設備之間的數據交換可同時進行.異步傳輸是主機上的pinned memory 通過不同流執行cudaMemcpyAsync()函數實現主機與設備之間的數據通信.同時多個流并發執行,當前流的數據傳輸結束之后,核函數立刻啟動,同時另一個流開始執行數據傳輸,通過數據傳輸與計算重疊的執行,能夠很好地隱藏主機與設備之間的數據通信時間,進一步提高并行效率.由于在后面主機端進行近遠場外推時需要電場分量Ez以及磁場分量Hx的值,需要在時間迭代穩定后將設備端的值傳回主機,為了隱藏數據通信時間,在此用了6個異步流并發執行來實現異步傳輸功能.在拷貝時offset不僅包括了當前計算網格的數據長度,也包括了周圍相鄰網格(offset_boundary),這是因為當前網格的計算與周圍相鄰網格的值有關,如果相鄰網格沒有包括,這會導致當前一部分網格沒有進行迭代,這與全局存儲器和共享存儲器之間的數據傳輸方式是一樣的.

2數值仿真結果

本節將利用并行FDTD方法對海面與上方目標的復合電磁散射特性進行詳細的討論分析.為了保證FDTD的準確性和穩定性,空間步和時間步為Δx=Δy=Δ=λ/20與Δt=0.5×Δ/c,λ為入射波波長,c為真空中的光速.UPML層的厚度為10Δ.計算平臺如表1所示.

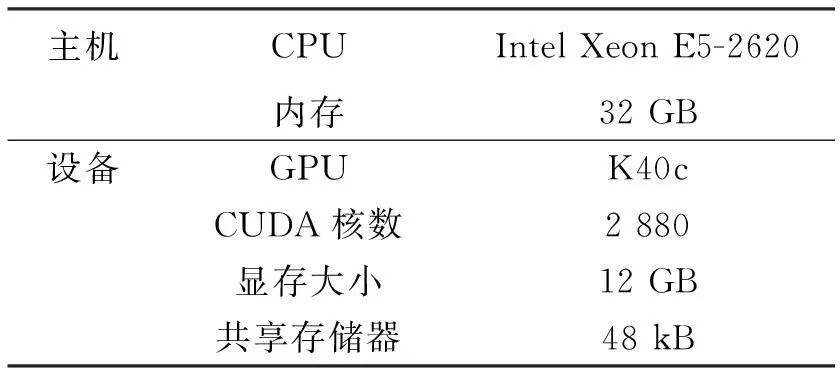
表1　計算平臺參數

為了驗證本文方法的正確性,以無限長導體圓柱與PM海面復合散射模型為例,與串行FDTD方法以及矩量法(Method of Moment, MoM)進行對比.圖3分別采用并行FDTD方法、串行FDTD方法和MoM計算TM 波和TE波入射下該模型的散射系數.其中,入射頻率f=1.0 GHz,入射角θi=40°,海面的長度L=4 096Δ,與入射頻率對應的海水介電常數εr=(72.0,84.0)(德拜模型)[17],海面風速U19.5=3.0 m/s,圓柱的高度H和半徑r分別為4λ和λ.由圖3可以看出,三種方法在大部分散射角范圍內都有很好的一致性,其中并行FDTD方法與串行FDTD方法吻合得非常好,兩者與MoM方法具有一定的差異,這是由FDTD方法和MoM算法本身導致的.

表2　不同計算網格的加速比

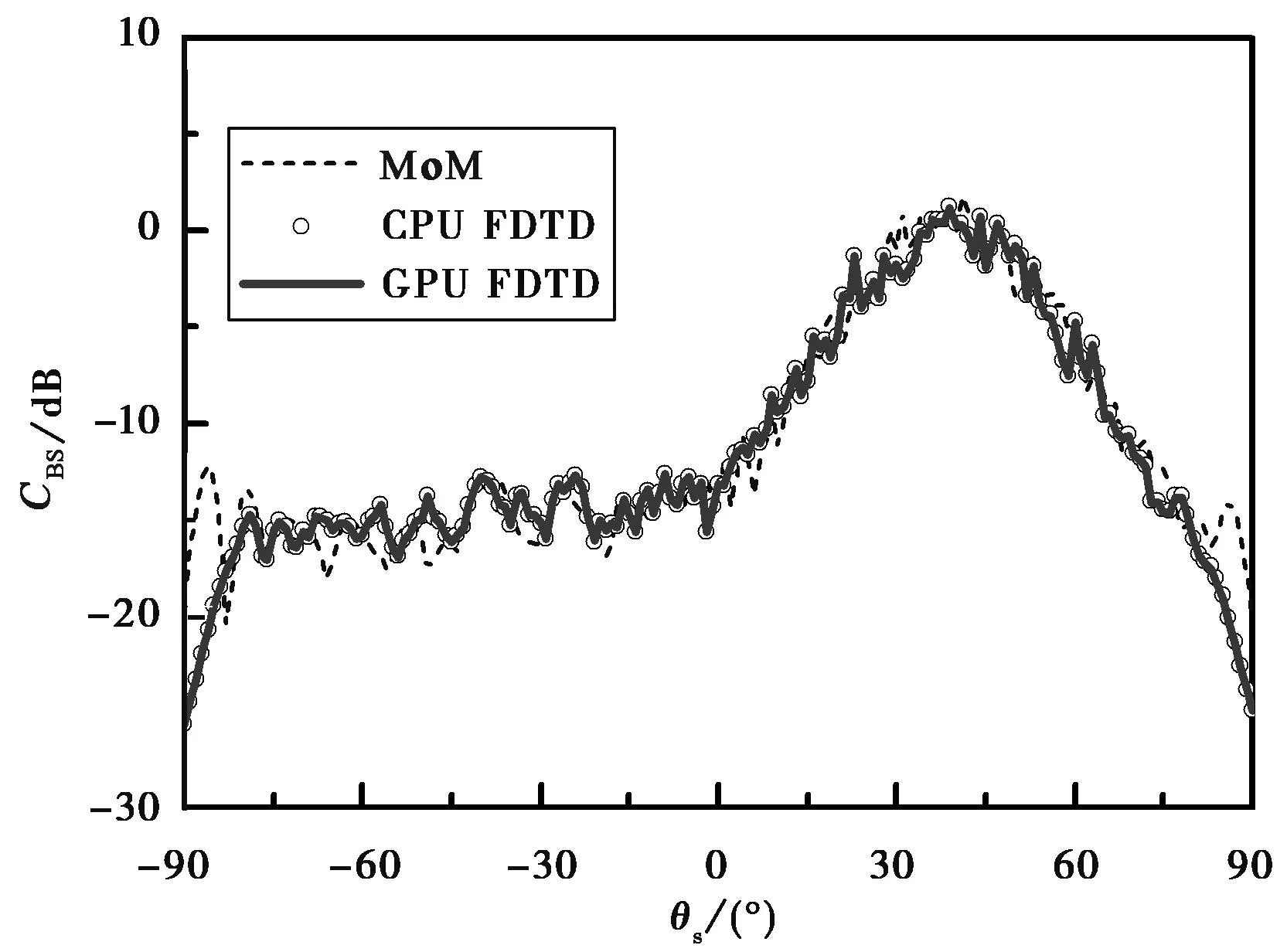
(a) TM

(b) TE圖3　海面與其上方圓柱復合散射并行FDTD、串行FDTD以及MoM的比較

為了驗證本文方法的效率,表2分別比較了不同網格數下的使用異步傳輸和沒有使用異步傳輸的加速比.從表中可以看出在一定網格數的范圍內,兩種傳輸模式的加速比隨著網格數的增加而逐漸增加,網格數增大到262 144Δ時,同步傳輸模式加速比減小,而異步傳輸模式下的加速比基本保持不變,并且在相同的計算網格的條件,異步傳輸模式的加速比比同步傳輸模式的加速比要大.隨著計算網格數的增加,GPU的計算單元逐漸被充分利用,所以加速比隨之增大,但當增大到262 144Δ時,由于數據量很大,同步傳輸模式下主機與設備之間數據交換時間的影響變得明顯,所以加速比較小; 而在異步傳輸模式下,主機與設備的通信時間被很好地隱藏,所以加速比基本不變,同時相同網格下的異步傳輸模式的加速比比同步模式下的加速比大,也說明了這個問題.從表中也可以看出,本文算法較串行方法具有很高的計算效率,特別是在計算電大尺寸問題時優勢明顯.

在計算準確與高效的基礎上,接下來,利用本文方法研究不同入射角下海面與上方漂浮類似艦船目標復合模型的電磁散射特性,如圖4所示,粗糙面長度16 384Δ,海面風速U19.5=3.0 m/s,入射頻率f=2 GHz,對應海水介電常數εr=(71.6,49.1),入射角θi分別為30°、45°、60°.吃水深度h=40Δ,從圖4中可以看出,對于TM和TE兩種入射情況,隨著入射角的增大,鏡向處散射減弱,并出現兩個峰值,非鏡向方向的散射增強,并且隨著入射角的增大,非鏡向方向有明顯的雙峰,特別當入射角θi=60°時,對于兩種極化,θs=-60°以及θs=-10°附近峰值明顯.

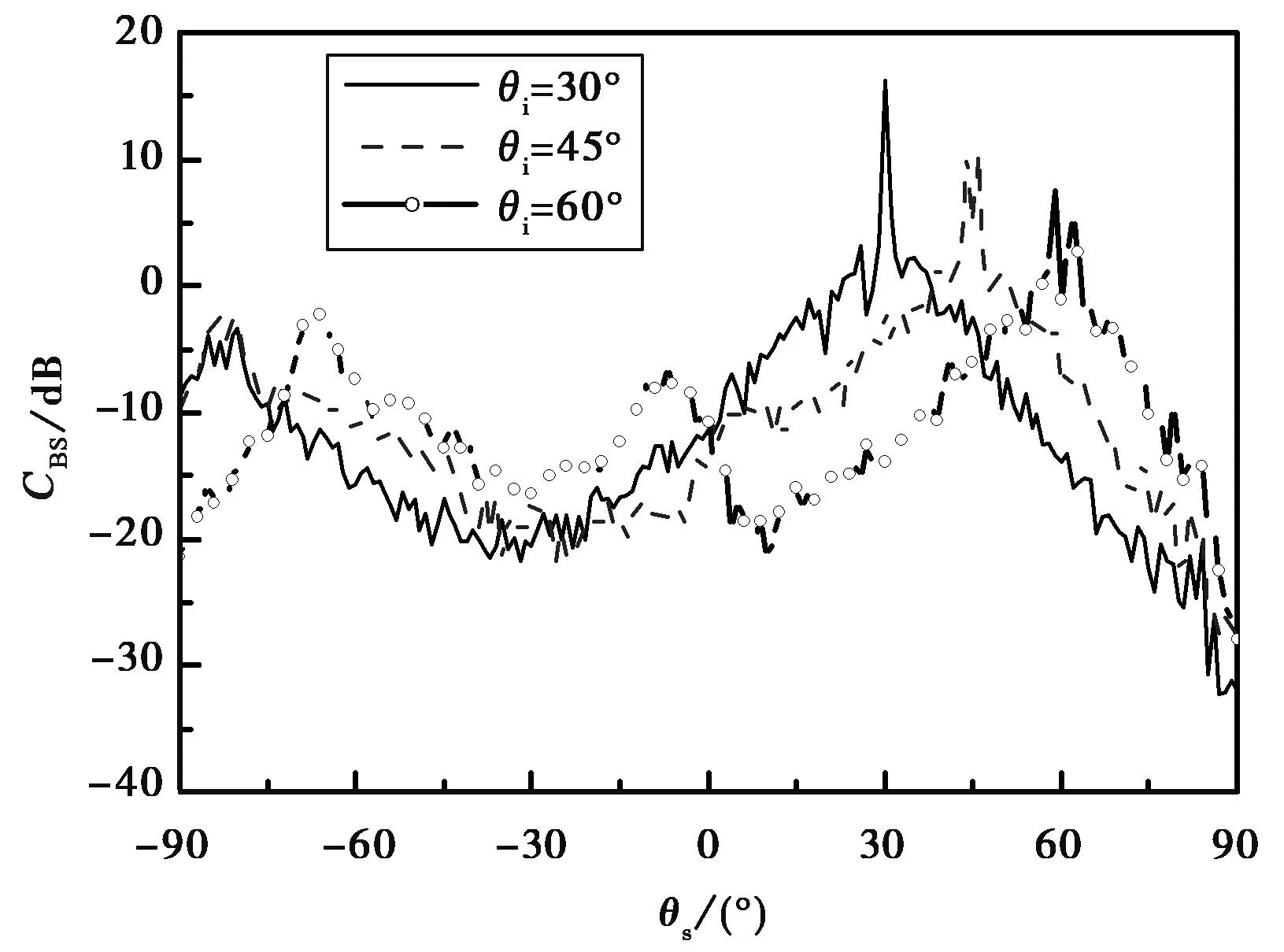
(a) TM

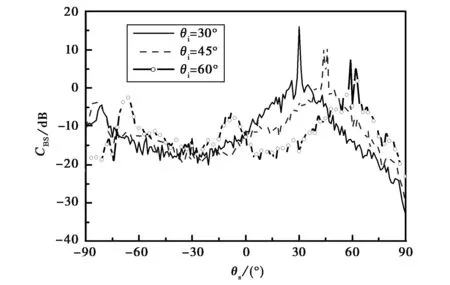
(b) TE圖4　不同入射角的雙站散射系數

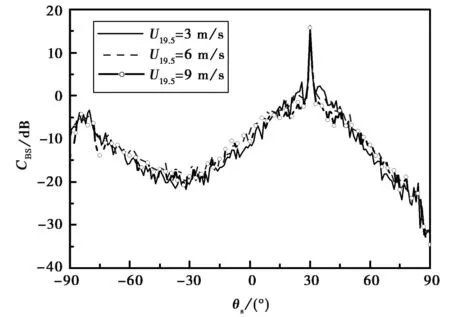
圖5給出了不同風速復合模型雙站散射系數隨散射角變化的結果.入射角θi=30°,風速U19.5分別為3 m/s、6 m/s、9 m/s,其他參數與圖4中的相同.對兩種入射而言,隨著風速的增加,鏡向附近的散射減弱.這是由于隨著風速的增加,海面變得粗糙,均方根斜率增加,進而導致鏡向方向散射減小.

圖6研究了一維PM海面與上方漂浮導體艦船目標的復合散射特性隨著艦船吃水深度變化的關系.其中,入射角θi=30°,艦船的吃水深度h分別為50Δ(0.375 m)、150Δ(1.125 m)、250Δ(1.875 m),其他參數與圖4中相同.從圖6中可以看出,對于兩種入射情況來說,隨著吃水深度的增加,非鏡向方向散射減小明顯,特別是在θs=-90°到θs=-30°之間,鏡向附近變化不是很明顯.這是因為隨著艦船吃水深度的增加,目標在海面上方的部分減小,艦船與海面之間的耦合作用在減弱,進而導致非鏡向方向的散射減弱.

(a) TM

(b) TE圖5　不同風速的雙站散射系數

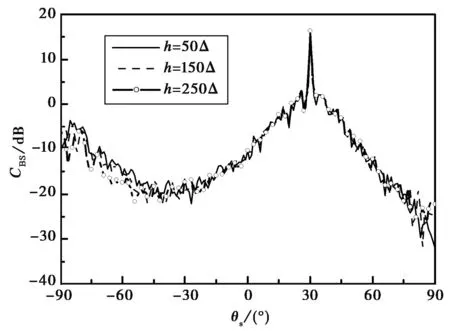
(a) TM

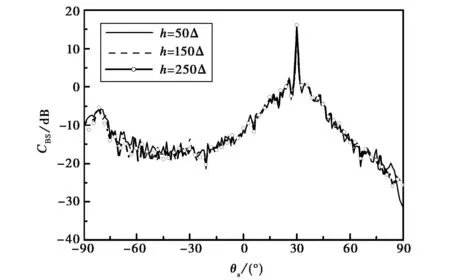
(b) TE圖6　不同吃水深度的雙站散射系數

3結論

本文將基于GPU的并行時域有限差分法引入到一維PM海面與上方漂浮艦船目標的復合電磁散射問題的計算中.從計算準確性與效率兩方面,驗證了保證串行方法高計算精度的前提下,與傳統串行方法以及MPI-based FDTD相比,在計算效率方面本文方法具有明顯優勢.在此基礎上,利用該方法進一步分析了海面與上方漂浮目標復合電磁散射特性.發現隨著入射角的增大,鏡向附近的散射減弱,非鏡向方向散射逐漸增強,甚至出現幾個峰值,這是由于艦船目標的影響較大;隨著風速的增加,鏡向附近雙站散射系數減小,非鏡向方向的雙站散射系數增大,這是由于風速的改變導致了海面粗糙面的變化;最后分析了艦船吃水深度對雙站散射系數的影響,數值結果表明,隨著吃水深度的增加,艦船與海面耦合作用減弱,導致非鏡向方向散射減弱.由于本文方法具有很高的計算效率,所以在計算電大尺寸目標與大尺度粗糙面復合散射問題時具有明顯優勢,所以利用GPU-based FDTD方法解決更為復雜耗時的三維目標與二維粗糙面的復合電磁散射問題將是我們今后研究工作的重點.

參考文獻

[1] VORONOVICH A G, ZAVOROTNY V U. Full-polarization modeling of monostatic and bistatic radar scattering from a rough sea surface[J]. IEEE transactions on antennas and propagation, 2013, 62(3): 1362-1371.

[2] LI Y, ZHANG Y Z, CHEN J, et al. Improved compact polarimetric SAR quad-pol reconstruction algorithm for oil spill detection[J]. IEEE geoscience and remote sensing letters, 2014, 11(6): 1139-1142.

[3] THORSOS E I. The validity of the Kirchhoff approximation for rough surface scattering using a Gaussian roughness spectrum[J]. The journal of the acoustical society of America, 1988, 83(1): 78-92.

[4] WANG Y Q, BROSCHAT S L. A systematic study of the lowest order small slope approximation for a Pierson-Moskowitz spectrum[J]. IEEE geoscience and remote sensing letters, 2011, 8(1): 158-162.

[5] THORSOS E I, JACKSON D R. The validity of the perturbation approximation for rough surface scattering using a Gaussian roughness spectrum[J]. The journal of the acoustical society of America, 1989, 86(1): 261-277.

[6] DURDEN S L, VESECKY J F. A numerical study of the separation wavenumber in the two-scale scattering approximation[J]. IEEE transactions on geoscience and remote sensing, 1990, 28(2): 271-272.

[7] GUAN B, ZHANG J F, ZHOU X Y, et al. Electromagnetic scattering from objects above a rough surface using the method of moments with half-space Green’s function[J]. IEEE transactions on geoscience and remote sensing, 2009, 47(10): 3399-3405.

[8] GUO L X, WANG A Q, CHAI C. Parallel fast multiple method for electromagnetic scattering from one-dimensional large-scale two-layered rough surfaces for large angles of incidence[J]. IET microwaves antennas and propagation, 2011, 5(15): 1813-1821.

[9] LI J, GUO L X, JIAO Y C, et al. Investigation on wide-band scattering of a 2-D target above 1-D randomly rough surface by FDTD method[J]. Optics express, 2011, 19(2): 1091-1100.

[10]張連波, 郭立新, 茍雪銀, 等. 三層粗糙面電磁散射的矩量法研究[J]. 西安電子科技大學學報, 2013, 40(6): 147-154.

ZHANG L B, GUO L X, GOU X Y, et al. Method of moment investigation on electromagnetic scattering from the three-layered rough interfaces[J]. Journal of Xidian University(natural science), 2013, 40(6): 147-154.(in Chinese)

[11]閻亞麗, 傅光, 龔書喜, 等.基于并行FDTD方法分析表面等離子波導的特性[J]. 電波科學學報, 2015,30(4): 668-672.

YAN Y L, FU G, GONG S X, et al. Analysis of a surface plasmonic waveguide using parallel finite difference time domain method[J]. Chinese journal of radio science, 2015, 30(4): 668-672. (in Chinese)

[12]SU X, WU J J, HUANG B, et al. GPU-accelerated computation for electromagnetic scattering of a double-layer vegetation model[J]. IEEE journal of selected topics in applied earth observations in remote sensing, 2013, 6(4): 1799-1806.

[13]JIANG W Q, ZHANG M, WEI P B, et al. CUDA-based SSA method in application to calculating EM scattering from large two-dimensional rough surface[J]. IEEE journal of selected topics in applied earth observations in remote sensing, 2014, 7(4): 1372-1382.

[14]THORSOS E I. Acoustic scattering from a “Pierson-Moskowitz” sea surface[J]. The journal of the acoustical society of America, 1990, 88(1): 335-349.

[15]FUNG A K, SHAH M R, TJUATJA S. Numerical solution of scattering from three-dimensional randomly rough surfaces[J]. IEEE transactions on geoscience and remote sensing, 1994, 32(5): 986-994.

[16]TAFLOVE A, HAGNESS S C. Computational electrodynamics: the finite-difference time-domain method[M]. Norwood: Academic, 2005: 297-365.

[17]KLEIN L A, SWIFT C T. An improved model for the dielectric constant of sea water at microwave frequencies[J]. IEEE transactions on antennas and propagation, 1977, 25(1): 104-111.

賈春剛(1986-),男,吉林人,博士研究生,研究方向為粗糙面及其與目標的并行加速計算.

郭立新(1968-),男,陜西人,西安電子科技大學物理與光電工程學院教授,研究方向為電磁/光波在復雜介質中的傳播和散射.

劉偉(1979-),男,陜西人,西安電子科技大學副教授,主要研究方向為電磁散射、微波遙感與參數反演.

作者簡介

中圖分類號TN011

文獻標志碼A

文章編號1005-0388(2016)01-0116-07

收稿日期：2015-01-05

賈春剛, 郭立新, 劉偉, 等. 并行FDTD方法在海面及其上方漂浮目標復合電磁散射中的應用[J]. 電波科學學報，2016,31(1):116-122. DOI: 10.13443/j.cjors.2015010501

JIA C G, GUO L X, LIU W, et al. Application of parallel FDTD to EM scattering from a target floating on sea surface[J]. Chinese journal of radio science，2016,31(1):116-122. (in Chinese). DOI: 10.13443/j.cjors.2015010501

資助項目: 國家杰出青年科學基金(61225002); 航空科學基金與航空電子系統射頻綜合仿真航空科技重點實驗室聯合資助(20132081015)

聯系人： 賈春剛 E-mail: cgjia@stu.xidian.edu.cn