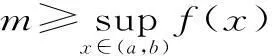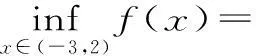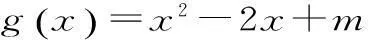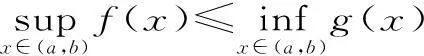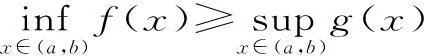淺談恒成立思想的推廣
?
淺談恒成立思想的推廣
■易如躍孫濤
恒成立問題是近年來高考的一大考點,每年高考各省市的試卷中都有其身影。本文將對如下恒成立論斷進行敘述和論證。
其一,已知函數f(x),x∈[a,b],若m 其二,已知函數f(x),x∈[a,b],若m>f(x)恒成立,則m>fmax(x)。 但此時問題就出現了,對于連續函數f(x),它在閉區間[a,b]上一定有最值,但在開區間(a,b)上就不一定有最值。若再用恒成立思想解題將遇到尷尬境界。為了解決此類問題,我們想到了數學分析中的確界原理。利用確界就可以解決最值不存在的問題。 定義:設f(x)為定義在區間(a,b)上的函數,若存在實數M(L)使得對一切x∈(a,b)都有f(x)≤M或f(x)≥L,則稱f(x)為(a,b)上有上(下)界的函數。M(L)稱為f(x)在(a,b)上的一個上(下)界。 對于函數f(x)在任何有限區間上都有界,根據確界原理可知,f(x)在區間(a,b)有上(下)確界。而所謂上確界即最小的上界,下確界即最大的下界。同時,若f(x)有最值,則最大值必為上確界,最小值必為下確界。 (1)恒成立思想的推廣。 例題設函數f(x)=-x2+2x,x∈(-3,2),若m 點評:通過此種方法,進一步驗證了恒成立思想的推廣對解決函數最值不存在的情況有較強的應用價值,同時也為問題的解決提供了理論支持。 方法二:由題可知,m<-x2+2x,即x2-2x+m<0在(-3,2)上恒成立。 點評:本方法是對二次函數圖像性質的進一步應用,旨在培養學生的數形結合思想。 (2)恒成立思想的進一步推廣。 方法三:由題可知,m<-x2+2x,即2x-m>x2在(-3,2)上恒成立。 令g(x)=2x-m,h(x)=x2,顯然g(x)在(-3,2)上無最小值,h(x)在(-3,2)上無最大值。 點評:在函數無最值的情況下,恒成立思想的進一步推廣,給我們解決恒成立問題提供了思想方法。 本文通過對恒成立問題的進一步研究,將高等數學中的確界引入到問題的解決中來,通過實例驗證,發現此種思想為解決恒成立問題提供了理論支持。同時也為廣大考生解決此類問題提供了方法和思路。 作者單位:安徽省合肥新城高升學校