利用支架式教學模式改進高三課堂教學
——《直線與圓的位置關系》教學反思和改進案例

韓元彬

(廣東省深圳市西鄉中學，深圳 518102)

利用支架式教學模式改進高三課堂教學
——《直線與圓的位置關系》教學反思和改進案例

韓元彬

(廣東省深圳市西鄉中學，深圳 518102)

支架式教學(Scaffolding Instruction)是建構主義的一種教學模式．它是一種以學生為中心，利用情境、協作、會話等學習環境要素充分發揮學生的主動性、積極性和首創精神，最終達到使學生有效地實現對當前所學知識的意義建構目的的教學方法．本文將支架式教學與數學教學相結合，教師通過支架作用不停地將學生的智力引導到更高的水平，不斷建造新的能力．本文利用建構主義學習理論“支架式教學”指導高三復習課《直線與圓的位置關系》，進行了支架式教學的應用探索,收到了明顯的教學效果．

支架式教學 高中數學教學 應用探索

一、理論依據

支架式教學(也稱為“腳手架式教學”或“支撐點式教學”)是一種教學模式，源于蘇聯心理學家維果茨基的“社會建構主義”理論和他的“最近發展區”理論．支架式教學是建構主義的一種教學模式．支架原本指建筑行業中使用的腳手架，在這里用來形象地描述一種教學方式：學生被看作一座建筑，學生的“學”就是在不斷地、積極地建構自身的過程；而教師的“教”則是為學生搭建一個必要的腳手架，支持學生不斷地建構自己．

支架式教學法主要由“復習舊知，搭腳手架”“創設情境，引入課題”“合作學習，探索研究”和“回顧反思，效果評價”四個部分組成．從支架的表現形式來看，常見的學習支架可以分為范例、問題、建議、工具、圖表等．

二、案例背景

《直線與圓的位置關系》是高考命題的熱點之一，知識點多，位置關系多．以往的教學是先復習點與圓的位置關系、直線與圓的位置關系、圓與圓的位置關系、圓的性質，再分位置關系的判斷、圓的切線、弦長問題、綜合問題等題型進行方法講解．這樣處理不僅花費的時間多，還不能激發學生的學習興趣，學生很難將知識點關聯起來解決問題，特別是圓的幾何知識更不易想到．而數形結合思想是解析幾何的核心思想，圓的問題用幾何法解更優越，因此本節復習時要突出幾何法，了解學生學習的困難點，搭建一些有效的支架，以激起學生的求知欲，讓學生的潛能得以發展．本文筆者以支架式教學理論為依托，對一些教學環節進行了改進，通過搭建一系列支架，構建知識間的聯系，降低了探索難度，最大程度地提高了教學效率，取得了良好的教學效果．

三、案例改進

1.復習舊知，搭腳手架

圍繞當前學習主題，設計了三層“最近發展區”，引出所要復習的知識點．

問題：已知直線方程和圓的方程，怎樣求直線與圓的相交弦長？

方法二：可以給學生搭一個支架，借助直線方程將兩點間距離公式簡化為只與橫坐標或縱坐標有關．學生立馬想到用直線方程y=kx+b帶入消元,

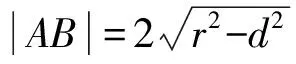
至此圍繞求直線與圓的相交弦長的學習主題，利用“最近發展區”進行了兩次搭建支架的設計，學生對求弦長的方法有了比較全面的了解，并進行了知識構建．

2.創設情境，引入課題

創設問題情境，讓學生明確本節課的要求，設問懸疑，激發學生的學習興趣．教師在教學過程中，充分利用學生的好奇心，有意識地營造“問題解決”的氛圍，培養學生的質疑精神，促使學生對新事物產生興趣，自覺主動地觀察事物，從而找到問題的特點和解決思路，就能點燃他們的思維火花．

例：過原點O作圓x2+y2-6x-8y+20=0的兩條切線，設切點分別為P，Q，則線段PQ的長為________．

此題包含了直線與圓的位置關系中的相切和相交，涉及圓的切線方程、切線長、切線夾角、切點弦方程等知識．由此題引入本節課的學習，能全面地考查本節課的核心內容，有利于激發學生的學習興趣．

3.合作學習，探索研究

由前面的復習，學生知道要求線段PQ的長，關鍵是要求出PQ的直線方程，容易想到先求切線方程，再求P，Q的坐標．

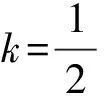
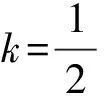
此法思維量小，運算量較大．

圖1

解法二：如圖1，引導學生觀察CQ⊥OQ,CP⊥OP，發現C,P,O,Q四點共圓，OC為圓的直徑，可以求出外接圓方程，PQ即為兩圓的公共弦，兩圓方程作差即得PQ的直線方程.

此法借助四點共圓和弦心距公式簡化了計算．

解法三：我們還可以充分挖掘圓的幾何特點，利用平面幾何知識來解決．由題目條件可以證出OC⊥QP，借助此條件求PQ的長.

解法四：已知∠PCO的正余弦值由倍角公式還可以求出∠PCQ的余弦值.那么可以借用∠PCQ余弦值來求PQ的長嗎？學生得出余弦定理的解法，PQ2=CQ2+CP2-2CQ·CPcos∠PCQ.

由以上四種方法進行比較，學生很直觀地體會到圓的問題用幾何法解更優越．

4.回顧反思，效果評價

本節課師生一起通過對一道高考題的研究，將圓的切線方程、切線長、切線夾角、切點弦方程等知識點的復習融入問題的探索過程中，避免單一枯燥的訓練．教師以一個個問題為支架，引導學生由煩瑣的代數解法，到幾何解法，進而拓展到三角解法和余弦定理解法，將學生的思維由一個高度推向另一個高度，激發了學生的思維火花，培養了學生的創新精神和實踐能力．

新的課程標準特別提倡學生動手實踐、自主探究與合作交流等學習方式．改進后的課堂教學以問題為支架層層深入、由淺入深、由表及里、環環相扣，突破了教學重點和難點，實現了三維一體的教育目標.同時也調動了學生的學習激情，以知識為載體，讓學生體驗探究的過程，培養了學生的觀察能力、探究能力和合作能力，轉變了學生的學習方式，關注能力發展．

[1]王海珊.教與學的有效互動——簡析支架式教學[J].福建師范大學學報(哲學社會科學版),2005(1).

[2]劉杰.支架式教學模式與課堂教學[J].貴州師范學院學報,2010(3).

[3]洪樹蘭.數學“支架式教學”研究[D].昆明：云南師范大學,2006.

(責任編輯：李 珺)