重溫數學家發現之旅 讓數學課堂回歸本真

吳艷華

[摘 要] 本文結合蘇科版八年級上冊第三章第一節“勾股定理（第一課時）”的課堂實錄，從數學課堂教學的教學情境、數學課堂教學中的自主學習兩個方面談了如何讓數學課堂回歸本真，以實現數學課堂的扎實有效.

[關鍵詞] 數學課堂；回歸本真；勾股定理

回歸本真，是指還原事物的本質. 數學課堂應該抓住數學的本質，重視數學本質的揭示，圍繞數學本質開展活動，運用平和、樸實的組織方式展開教學，讓數學課堂“回歸本真”，以實現扎實有效的數學教學. 接下來就結合蘇科版八年級上冊第三章第一節“勾股定理（第一課時）”具體談談如何實現數學課堂回歸本真.

背景介紹

筆者有幸能夠于5月18日在蘇州星海實驗學校開設一節市級公開課，內容是八年級上冊第三章第一節“勾股定理（第一課時）”，時間40分鐘.

設計思路

本節課將采取觀察、操作、猜想、歸納的形式，有組織、有目的地引導學生參與到活動中，通過小組合作探索、交流、歸納，由淺入深，由特殊到一般，提出問題，自主探索，合作交流，有效地激發學生的思維積極性.

教學目標

1. 知識與技能

（1）讓學生經歷從“數”到“形”再由“形”到“數”的轉化過程，經歷探求三個正方形面積間的關系轉化為三邊數量關系的過程；并從過程中讓學生體會數形結合思想，發展將未知轉化為已知，由特殊推測一般的合情推理能力.

（2）讓學生經歷拼圖實驗、計算面積的過程，在過程中培養獨立思考、合作交流的學習習慣；讓各類型的學生在這些過程中發揮自己的特長，通過解決問題增強自信心，激發學生學習數學的興趣. 通過教師的介紹，感受勾股定理的文化價值.

（3）能說出勾股定理，并能用勾股定理解決簡單的問題.

2. 過程與方法

讓學生經歷觀察、操作、猜想、歸納的數學思想，體會數形結合和特殊到一般的思想方法.

3. 情感態度與價值觀

通過實踐、操作、猜想，使學生深刻感受數學知識的發生、發展過程. 介紹中國古代有關勾股定理研究方面取得的偉大成就，激發學生的愛國情感.

教學重點

勾股定理的探索過程.

教學難點

將邊不在格線上的圖形轉化為邊在格線上的圖形，以便于計算圖形的面積.

教學過程簡錄

環節一：合作交流、課前試水

課前讓學生先完成課前任務單，并利用上課前5分鐘的時間，在組內進行交流. （對于一部分明顯錯誤的猜想，在小組內以互幫互助的形式解決；尚不能解決的問題填寫在“我的困惑”一欄里，留待課堂上共同解決）

課上開門見山展示各小組的學習成果.

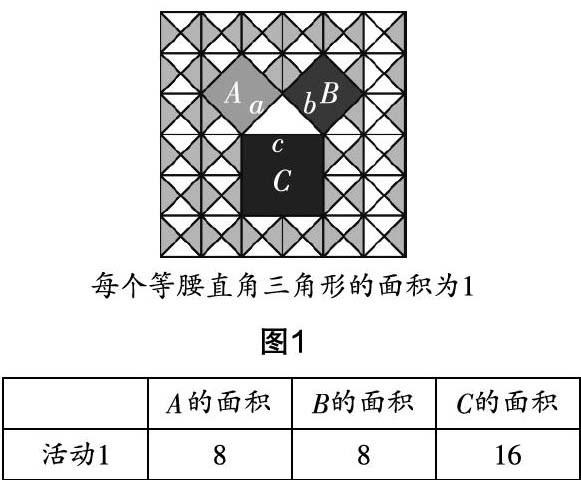
1. 活動1：觀察圖形探究等腰直角三角形三邊的關系

師：你們是怎么求正方形的面積的？

生：數它含有幾個等腰直角三角形.

2. 活動2：觀察圖形并探究一般直角三角形三邊的關系

師：你們是怎么求正方形的面積的？

生：A，B可以通過數格子（或者數邊長），C的面積可以采用割或補的方法來求. （學生上臺展示，割和補的方法求面積是本節課的一個難點）

師：前面我們通過數格子、割或補的方法求出了正方形的面積，那要是沒有網格圖你還能求出正方形的面積嗎？根據前面的觀察和猜想，完成下面的練習.

練習1 求下列各圖中未知數x，y，z的值.

評析 教學情境是為教學服務的，它是聯系現實生活與數學邏輯之間的重要橋梁. 圖1其實就是古希臘數學家畢達哥拉斯有一次在朋友家吃飯的時候，看到的朋友家的地磚圖形. 這引起了他的注意，并對此展開了研究，最終發現了勾股定理. （通過創設情境，讓學生重溫科學家的發現之旅）當然，在創設情境時，我們從最特殊的等腰直角三角形到一般直角三角形，再到沒有網格的一般直角三角形，體現了數學從特殊到一般的數學思想.

師：通過以上的實驗、操作、計算，我們發現以直角三角形的各邊為邊所作的正方形的面積之間有什么關系呢？直角三角形的三邊又有怎樣的數量關系？同學們自己總結結論.

生：較小的兩個正方形的面積和等于較大的正方形的面積；直角三角形兩條直角邊的平方的和等于斜邊的平方.

點評 這一環節只是引導學生通過前面的觀察進而得出猜想，既然是猜想，那么即使猜錯了，也不要急于否定，而是要充分肯定學生的“研究成果”. 至于它的正確性，可以留到后面進行驗證.

環節二：動手操作，驗證結論

師：但這些僅僅是我們的猜想，還需要進行驗證. 請同學們一起來做個數學小實驗. 以小組為單位，請同學們用桌上4個全等的直角三角形拼出一個正方形（可以有空隙），然后把它貼到白紙上. 聽清楚要求后再開始動手操作. （學生動手操作，下面是他們的部分作品）

師：對于圖6，從整體來看，這個大正方形的面積如何表示？從局部看，大正方形的面積又可以怎么表示？

生：大正方形的面積從整體看是c2，從局部看是4個小直角三角形的面積加上中間空白的正方形的面積.

師：對于圖7，從整體和局部兩個角度來看，也能得出a2+b2=c2.

評析 動手實踐、自主探究與合作交流是新課程積極倡導的學習方式，它與傳統的學習方式最大的不同在于，教師要更多地讓學生自主學習，通過教師的組織和引導，讓學生親歷操作實驗、觀察現象、提出猜想、推理論證等活動，獲得知識、活動經驗，感悟數學思想.

師：其實早在公元3世紀，我國的數學家趙爽就用這4個相同的直角三角形拼成了圖6，驗證了我們的猜想，這個圖被稱為“弦圖”. 西方的畢達哥拉斯用4個相同的直角三角形拼成了這樣一個正方形（圖7）進行了驗證. 所以我們現在可以總結歸納了，即直角三角形兩直角邊的平方和等于斜邊的平方.

師：在古時候，人們把較短的直角邊稱為勾，較長的直角邊稱為股，斜邊稱為弦，所以這個定理被稱為勾股定理. 在西方，也被稱為畢達哥拉斯定理. （引出今天的課題）這就是我們今天要學習的“勾股定理”.

師：我們回過頭來看看我們課前的練習和猜想是否正確.

環節三：學以致用，解決問題

師：接下來我們來簡單應用一下.

練習2 求下列直角三角形中未知邊的長.

評析 能應用勾股定理求直角三角形中未知邊的長，這是本節課的基本目標.

師：其實勾股定理在我們現實生活中的用途非常大，它可以幫助我們解決很多實際問題，接下來我們來看看下面三個練習.

練習3 地震中，一座鐵塔在離地40 m的地方被攔腰折斷了，鐵塔的頂部落到離架子底部30 m的地方，你能求出這個鐵塔原來的高度嗎？（圖10）

評析 在研究了勾股定理在數學應用的基礎上進一步研究其在實際生活中的應用，能讓學生感受到數學源于生活，又應用于生活，并積累利用數學知識解決日常生活實際問題的經驗和方法.

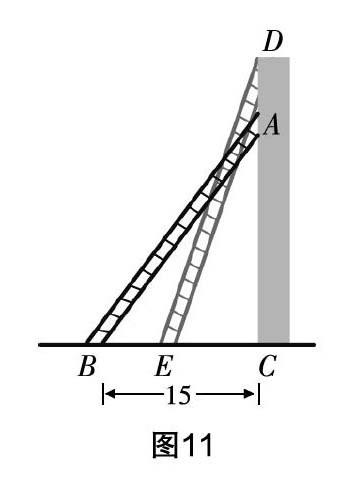
練習4？搖 火災中，一架救援梯子長25 m，梯子的底部離建筑物15 m，此時，梯子最高能到多少米？如果每層樓高4 m，要想救上一層的人，梯子的底部要向樓的方向推進多少米？（圖11）

評析 難度有所提升，特別是第2小問，進一步發展學生有條理思考和有條理表達的能力，體會數學的應用價值.

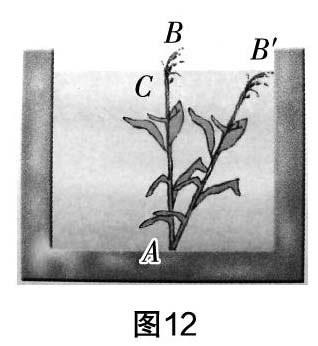
練習5 《九章算術》中的引葭赴岸問題：“今有池方一丈，葭生其中央. 出水一尺，引葭赴岸，適與岸齊. 問水深、葭長各幾何. ”題意是：有一個邊長為10尺的正方形池塘，一棵蘆葦AB生長在它的中央，高出水面部分BC為1尺. 如果把該蘆葦沿與水池邊垂直的方向拉向岸邊，那么蘆葦的頂部點B恰好碰到岸邊的B′處. 問水深和蘆葦長各多少. （圖12）

評析 三個生活實際問題難度層層遞進，如何把實際問題轉化成數學問題，并用數學方法解決，體現了數學應用的本真性. 在運用勾股定理解決實際問題的過程中，感受數學的“轉化”思想.

環節四：師生小結，共同進步

1. 說說本節課發現勾股定理的過程.

特殊情況研究→一般情況研究→猜想→驗證→歸納定理

2. 你對直角三角形中邊、角之間的關系有何全新的認識？

角：∠C=90°，∠A+∠B=90°.

邊：任意兩邊之和大于第三邊；兩直角邊的平方和等于斜邊的平方.

教學反思

本節課通過觀察、猜想、操作、歸納，還原了勾股定理發現、驗證的過程. 在教師的組織、引導下，讓學生積極主動地參與到教學活動中，通過小組合作探索、交流、歸納，由淺入深，由特殊到一般，提出問題，自主探索，合作交流獲得知識，學生真正成為學習的主人. 在這個過程中，無論是基礎知識、基本技能這些顯性知識，還是數學思想、數學活動經驗這些隱性知識，都會得到進一步的強化. 于是乎，學生個體的數學素養隨之提升.

列寧曾經說過，教學的藝術，是人類最偉大的藝術. 在數學課堂這片廣闊的藝術天地中，如果能通過“數學化”的途徑進行教學，讓數學課堂“回歸本真”，那么一定會使我們的數學課堂散發出無窮的數學魅力.