有關折弦定理的幾個推論
吳文龍
摘 要:折弦時常應用于初中數學競賽試題中,對數學競賽的輔導與學習具有良好的作用,證明了著名的“阿基米德折弦定理”的逆定理及幾個推論,以后可直接運用。
關鍵詞:折弦;定理;推論
在同一圓上有公共點的兩條弦組成一條折弦。折弦時常應用于初中數學競賽試題中,對數學競賽的輔導與學習具有良好的作用,值得研究和探討。下面討論幾個有關折弦的命題。
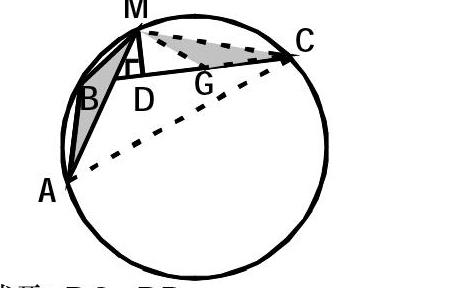
命題1:如圖,若弦AB、BC組成⊙O的一條折弦,BC>AB,D是弧ABC的中點,DE⊥BC,垂足為E,則E是折弦ABC的中點,即CE=BE+AB.
此命題即著名的“阿基米德折弦定理”。此命題的證明是不難理解的,有此定理的11種證法。
該定理常規的證明方法有以下幾種:
阿基米德折弦定理證法1:補短法
如圖,延長DB至F,使BF=BA
∵M是弧ABC的中點
∴∠MCA=∠MAC=∠MBC
∵MBAC四點共圓
∴∠MCA+∠MBA=180°
∵∠MBC+∠MBF=180°
∴∠MBA=∠MBF
∵MB=MB,BF=BA
∴△MBF≌△MBA
∴∠F=∠MAB=∠MCB
∴MF=MC
∵MD⊥CF
∴CD=DF=DB+BF=AB+BD
阿基米德折弦定理證法2:截長法
如圖,在CD上截取DG=DB
∵MD⊥BG
∴MB=MG,∠MGB=∠MBC=∠MAC
∵M是弧ABC的中點
∴∠MAC=∠MCA=∠MGB
即∠MGB=∠MCB+∠BCA=∠MCB+∠BMA
又∠MGB=∠MCB+∠GMC
∴∠BMA=∠GMC
∵MA=MC
∴△MBA≌△MGC
∴AB=GC
∴CD=CG+GD=AB+BD
阿基米德折弦定理證法3:垂線法
如圖,作MH⊥射線AB,垂足為H
∵M是弧ABC的中點
∴MA=MC
∵MD⊥BC
∴∠MDC=90°=∠H
∵∠MAB=∠MCB
∴△MHA≌△MDC
∴AH=CD,MH=MD
又∵MB=MB
∴Rt△MHB≌Rt△MDB
∴HB=BD
∴CD=AH=AB+BH=AB+BD
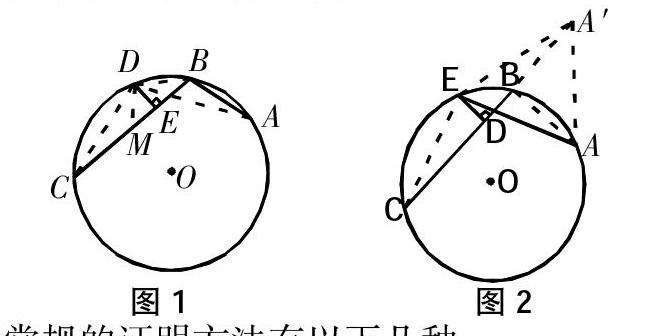
命題2:如圖,若弦AB、BC組成⊙O的一條折弦,BC>AB,D是折弦ABC的中點,DE⊥BC,垂足為E,則E是弧ABC的中點,即CE=AB+BE.
此命題是命題1的逆命題,就稱“阿基米德折弦逆定理”。證明也不難理解,延長CB到A′,使BA′=BA,連接CE、EA′、AA、EA即可得證。
這兩個定理體現了數學的和諧美,由這兩個定理不難聯想到以下兩個有用命題。
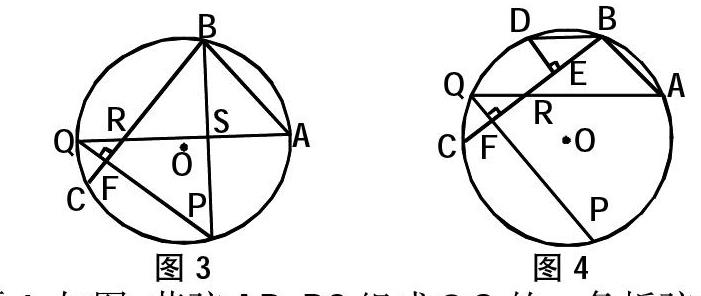
命題3:如圖,若弦AB、BC組成⊙O的一條折弦,BC>AB,P是弧AC的中點,PQ⊥BC,垂足為F,交⊙O于Q,AQ交BC于R,則
(1)CF=RF;
(2)PB垂直平分AR;
(3)AB=BR.
證法:連接CQ,先證△CQF≌△RQF,得到CF=RF;
再證△ABS≌△PBS,得到PB垂直平分AR,AB=BR.
命題4:如圖,若弦AB、BC組成⊙O的一條折弦,BC>AB, D是弧ABC的中點,P是弧AC的中點,DE⊥BC,垂足為E, PQ⊥BC,垂足為F,交⊙O于Q,AQ交BC于R,則
(1)BE=CF;
(2)AB=EF;
(3)DE∥QF, DE=QF;
(4)DB∥AQ.
此命題可由命題1和命題3加以證明,證明過程略。
參考文獻:
[1]周春荔,張寧生.數學奧林匹克教材(普及版)[M].北京:首都師范大學出版社,1994.
[2]張昕.一道初中競賽題的證法探討[J].中學數學教學參考,1999(3):32-33.
?誗編輯 孫玲娟

