基于二部圖匹配的數獨求解程序

張贊波

摘要：數獨游戲是一個具有組合數學背景的智力游戲。在本文中，我們設計一個基于圖論的數獨求解程序。我們將數獨的狀態對應為二部圖，數獨的求解對應為二部圖的匹配求解。運用二部圖的匹配理論和算法解決數獨問題。從網絡上搜集的一些數獨題目作為算法的試驗數據。對于一些初始狀態中含有比較多的數字的題目，我們的程序能夠解答出最終答案。

關鍵詞：匹配 二部圖 數獨

中圖分類號：TP3-0 文獻標識碼：A 文章編號：1007-9416（2016）07-0046-02

Abstract：Sudoku is a combination of mathematical background of the intelligence game. In this paper， we design a Sudoku solver based on graph theory. We will state for the two corresponding Sudoku Sudoku for solving the corresponding graph， matching to solve the two plans. Using the matching theory and algorithm of the two plans to solve Sudoku problem. Some Sudoku collected from the network as the experimental data of the algorithm. For some of the initial state of the problem contains a number of numbers， our program can answer the final answer.

Key Words：matching two figure Sudoku

1 背景和基本定義

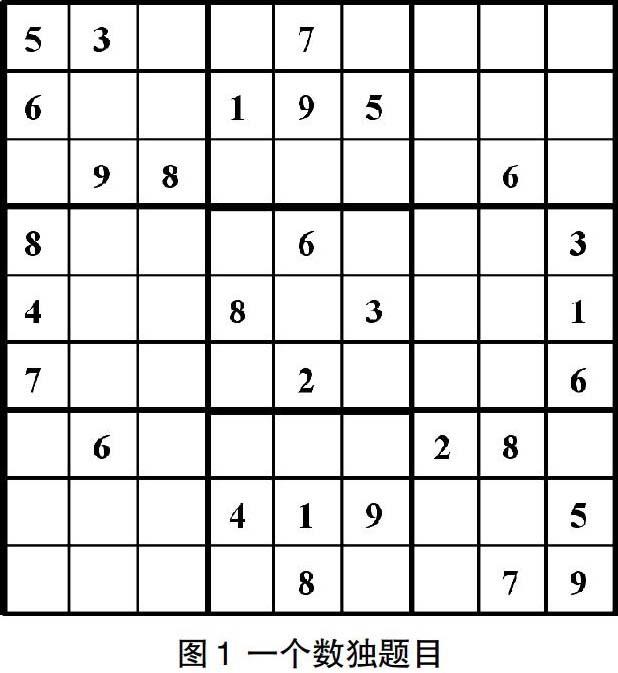
數獨游戲是一個具有組合數學背景的智力游戲。一個數獨題目在一個9 9的方陣上設計和解答。該方陣被劃分成9個3 3的稱為盒子（box）的小方陣，如圖1中粗線所示。方陣的每一個格子恰好可以填入1到9的某一個數字。在游戲的最開始，一部分方格已經填上了數字，如圖1。游戲的目標是把方陣余下的每一個格子也填上數字，使得每行，每列和每個盒子的9個格子中都恰含有數字1到9。

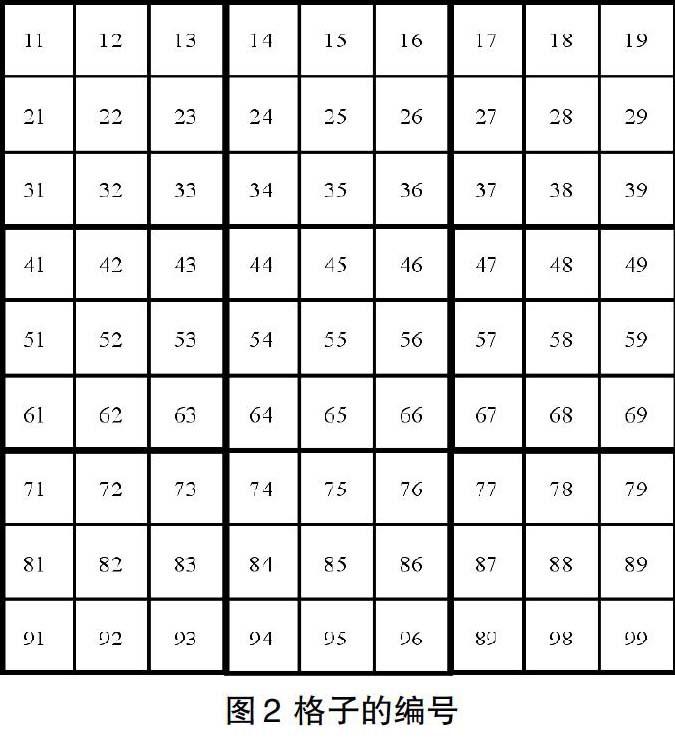
我們對方陣的格子如圖2進行編號。首先我們對方陣的行和列進行編號。方陣的行，自上而下編號為第1行至第9行。方陣的列，自左到右為編號第1到第9列。然后我們對格子進行編號。位于第r行第c列的格子編號為 （r， c），1 ≤ r， c ≤ 9。由于空間所限，在圖2中我們將格子的編號 （r， c） 簡寫成rc。

在本文中，我們運用二部圖的匹配理論來求解數獨題目。下面先給出我們將用到的一些圖論的基本概念。一個圖G=（V， E） 包含一個頂點集合V和一個邊集E，E是V的元素的二元組集合。一條邊e所包含的兩個頂點元素稱為e的端點。我們討論的圖都是簡單的，也就是不存在一條邊，它的兩個端點相同；同時，兩個端點之間最多只有一條邊。一個圖稱為二部圖，如果它的頂點集合可以分成兩個子集U和W，使得它的每一條邊的兩個端點都分別落在U和W中。或者換句話說，在U和W內部沒有邊。我們把這樣的二部圖記為G=（U， W）。若|U|=|W|，則稱此二部圖為平衡二部圖。若U中的每個點都與W中的每個點相鄰，稱此二部圖為完全二部圖。如果一個圖中的兩條邊具有公共的端點，則稱它們相鄰。一條邊的兩個端點也稱為相鄰的。與一個頂點相鄰的所有頂點的集合稱為它的鄰居。匹配是指圖的一個兩兩不相鄰的邊集。我們稱一條邊覆蓋它的端點。如果一個匹配中的邊覆蓋了圖的所有頂點，則稱此匹配為完美匹配。顯然，具有完美匹配的二部圖必須是平衡二部圖。

一條邊和它的端點稱為互相關聯。一個頂點關聯的邊的條數，或等價地它的鄰居的個數，稱為它的度數。取圖G的頂點集合V的一個子集V1，構造一個圖G1=（V1， E1），其中E1是G中所有兩個端點都落在V1中的邊的集合，圖G1稱為頂點子集合V1的導出子圖。

2 基于匹配理論的數獨求解

我們定義一個動態的二部圖G=（U， W），其中U={（1， 1）， （1， 2）， …， （9， 9）}是數獨方陣中格子的集合，而W={1， 2， 3， 4， 5， 6， 7， 8， 9}是格子中可以填入的數字的集合。在一個數獨題的最終解中，所有81個格子中的數字都已經確定。如果數字d W填入方格（r， c） U中，那么我們在G中連結d與（r， c）。這樣共產生81條邊。U中的每一個頂點恰發出一條邊到W集合中填在頂點對應的方格中的數字。從而U中頂點的度數全部為1。而W中每一個數字在方陣中恰出現9次，因此W中代表每一個數字的頂點的度數全部為9。

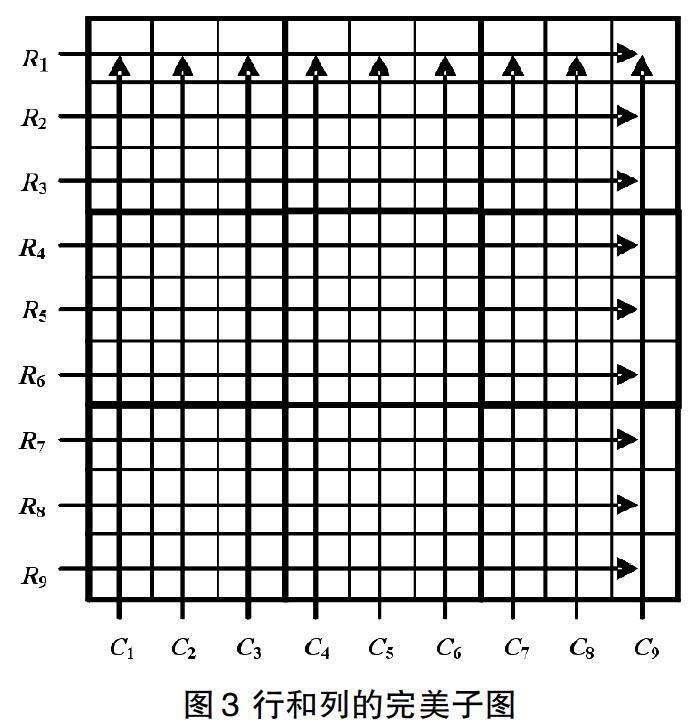
取所有位于方陣第r（1 ≤ r ≤ 9）行的格子所組成的U的子集，該子集與W的并集構成G的一個頂點集，記該頂點集的導出子圖為Rr。對于方陣的第c（1 ≤ c ≤ 9）列，我們類似定義該列的格子與W的并集在G中的導出子圖Cc。而對于方陣的第b（1 ≤ b ≤ 9）個盒子，我們也類似定義盒子中的格子與W的并集在G中的導出子圖Bb。稱上述27個子圖為完美子圖。如圖3與圖4所示。對一個數獨題的最終解而言，每行，每列和每個盒子恰含有數字1到9，意味著G的完美子圖的邊集恰好構成該子圖本身的一個完美匹配。

在G的初始狀態，我們連結所有的頂點（r， c） U與頂點d W，使得G成為一個完全二部圖。在我們解決數獨方陣的推理過程中，我們不斷通過現已填入的數字，排除其他方格中可能填入的數字。以此為根據，我們可以刪除G的邊：如果在某一步，我們排除了方格（r， c） U中填入數字d W的可能，則刪除掉（r， c）與d之間的邊。這樣圖G的邊的狀態便記錄了我們推理的中間結果。反之，我們可以從圖G的完美子圖根據匹配理論進行推導，從而排除某些方格中填上某個數的可能。當G最終剩余81條邊，U中的每一個頂點的度數為1，W中的每一個頂點的度數為9時，我們就得到了數獨問題的最終解。

我們從G為完全圖的狀態開始。當給定一個數獨題目的初始狀態，即一個填入了部分數字的9 9的方陣，我們可以根據該狀態對G進行刪邊的操作。假設方格（r， c）中已經填上了數字d，其中d W，則我們可以去掉所有與（r， c）相關聯的邊，僅保留（r， c）與d之間的邊。此外，注意到（r， c）包含于3個完美子圖Rr，Cc和Bb，其中b = [r/3]*27+（r mod 3）*3+[c/3]*9+（c mod 3），我們可以去掉子圖Rr，Cc和Bb中除了（r， c）以外其它格子與d之間的邊。對每一個已經填上數字的方格（r， c）完成了上述刪除操作以后，我們就用圖G表示出數獨題目的初始狀態。

在以圖的匹配建模以后，我們最終的目標是使得圖G剩下81條邊，而每個完美子圖的邊集恰剩下一個完美匹配。因此，解數獨題的過程，就是不斷根據現有的邊進行推理，刪去當前圖G的某一個完美子圖中所有的不可能包含于任何完美匹配的邊。我們把一個圖中不含于任何完美匹配的邊稱為禁止邊。因為一條邊包含于3個完美子圖，當我們在一個完美子圖中刪去禁止邊，便會使得其它完美子圖的邊減少。因此，我們又可以在受影響的完美子圖中重新尋找禁止邊，將其刪去。數獨題目求解的過程，就是不斷的在完美子圖中刪去禁止邊，一直到確定所有方格中的數字。

為了進一步說明求圖的匹配與求解數獨題的邏輯推理的關系，我們以圖5的數獨局部狀態為例。在圖5中，由于（1， 2）和（3， 5）都為3，我們可以推知在B3之中，數字3必然位于第二行，即三個格子（2， 7），（2， 8）或（2， 9）之一（圖中以“*”號標注）。因此其它的六個格子（1， 7），（1， 8），（1， 9），（3， 7），（3， 8）和（3， 9）與3相連的邊應該刪去，而（2， 7），（2， 8）和（2， 9）則繼續有邊發向3。從圖G中看，我們的上述推理可以由匹配理論來完成，在R1中（1， 2）和3相鄰，從而可以刪除掉3與其它格子相連的邊。因此3和（1， 7），（1， 8），（1， 9）之間沒有邊相連。同理在R3中（3， 5）和3相鄰，從而可以刪除掉3與其它格子相連的邊。因此3和（3， 7），（3， 8），（3， 9）之間沒有邊相連。上述刪除掉的邊也屬于子圖B3，因此在B3中3只能和（2， 7），（2， 8）和（2， 9）相鄰。

3 算法的實現

圖G有27個完美子圖。在某一狀態，必定能夠從一個完美子圖中找到一些禁止邊，并將它們去掉。由于去掉了一個完美子圖的一些禁止邊以后，影響了其他完美子圖的結構，因而會在其他完美子圖中產生新的禁止邊，從而又可以在其他完美子圖中進一步尋找新產生的禁止邊。因此，我們算法的思路，就是循環地對圖G的27個完美子圖進行考察，刪掉它們的禁止邊。直到圖G剩下81條邊為止。

要求出一個二部圖的禁止邊，可以使用現有的算法，目前速度最快的算法（O（VE））可參見參考文獻[1]。但是，我們處理的僅僅是一個18個點的平衡二部圖，因此可以直接使用所謂蠻力（brute force）算法。Brute force算法對每一條邊執行以下操作：從圖中刪掉該邊及其兩個端點，驗證余下的子圖是否有完美匹配，從而判斷該邊是否禁止邊。而判斷二部圖是否有完美匹配則采用經典的匈牙利算法[2]。求二部圖所有禁止邊的集合的算法流程圖見算法1。求解數獨的主算法見算法2。

算法1：求二部圖G的禁止邊的集合。

輸入：二部圖G。

輸出：圖G的禁止邊的集合。

1對于每一條邊e E，執行如下操作2至4。

2從G中刪除e和e的端點。得到圖G-e。

3調用匈牙利算法判斷G-e是否有完美匹配。

4如果G-e沒有完美匹配，則標記e為G的禁止邊。

5輸出所有標記為禁止邊的邊e。

算法2：求解數獨

輸入：一個數獨游戲的初始狀態。

輸出：該數獨游戲的最終解。

1構建完全二部圖G。

2根據數獨游戲的初始狀態，刪除G的禁止邊，使得G對應于數獨游戲的初始狀態。

3重復以下步驟4至6，直到G的邊數等于81。

4對于c=1到9，調用算法1求解完美子圖Cc的禁止邊的集合，將其從Cc中刪除。

5對于r=1到9，調用算法1求解完美子圖Rr的禁止邊的集合，將其從Rr中刪除。

6對于b=1到9，調用算法1求解完美子圖Bb的禁止邊的集合，將其從Bb中刪除。

4 試驗和進一步工作

我們使用從網絡上搜集的一些數獨題目作為算法的試驗數據。對于一些初始狀態中含有比較多的數字（超過25個數字）的題目，我們的程序能夠解答出最終答案。但是對于一些比較困難的數獨題目，如西澳大學Gordon Royle教授收集的具有最小初始狀態（17個數字）的數獨題集，我們的程序不能求解出最終答案。因此，我們還需要進一步探討對算法的改進。

在文獻[3]中，作者在研究匹配覆蓋圖的過程中，定義了一個具有完美匹配的圖中的邊關于完美匹配的依賴關系（簡稱為邊的依賴關系）。對于兩條邊e和f，我們稱e依賴于f，如果每一個含有e的完美匹配一定含有f。我們認為，如果在算法中加入求解每一個完美子圖的邊依賴關系，并根據邊依賴關系作進一步推理，將很有可能提高我們的程序的求解能力，甚至有可能徹底解決所有的數獨問題實例。我們擬于下一步工作中根據這個思路對算法作進一步改進。

參考文獻

[1]Y.Li，& D.Lou.A new algorithm for determinating 1-extendable graphs： design and implementation. In IMECS，2327-2332，2007.3.

[2]L. Lovász， & M. D. Plummer，M.D.Matching theory （Vol. 367）. American Mathematical Soc.， 2009.

[3]de Carvalho， M. H.，Lucchesi，C.L.，& Murty，U.S. （2002）. On a conjecture of lovász concerning bricks：I.the characteristic of a matching covered graph. Journal of Combinatorial Theory， Series B， 85（1）94-136.