PBL模式下的高中數(shù)學微課教學研究
——以“不等式與數(shù)列求和教學”為例

☉江蘇省口岸中學高國圣

PBL模式下的高中數(shù)學微課教學研究
——以“不等式與數(shù)列求和教學”為例

☉江蘇省口岸中學高國圣

隨著新課程改革的日益深入，傳統(tǒng)的“滿堂灌”“填鴨式”教學模式已經(jīng)逐漸被“問題探究式”教學模式取代，PBL模式是一種新型教學模式，這是一種以問題為中心的教學模式，教師在“問題中心”下指導學生進行深入思考，結合自己所學知識提出新問題.微課教學與PBL模式相結合，能夠有效提高課堂教學學習效率，也有利于培養(yǎng)學生的自主學習探究能力.

一、PBL模式與微課教學形式分析

1.PBL模式

PBL模式是一種以問題為基礎的教學方法，教師圍繞教學目標，在問題指導下設計教學步驟，PBL模式下的課堂教學主要分為四個階段：課前準備階段、課堂階段、課后自學階段、課堂總結評價階段.下面我們將具體分析這種教學模式下的教學四階段：（1）課前準備階段.首先讓學生了解PBL模式有關知識、特點，教授學生學會使用這種教學模式發(fā)現(xiàn)問題并解決問題，增強其對PBL模式的認識與理解.PBL模式最突出的一個特征就是學生進行分組學習，學生分組時，應將小組規(guī)模、學生搭配及組內結構等考慮進去，小組人數(shù)最好控制在6人左右，搭配好性別、性格及成績比例，將知識與能力互補互助特點體現(xiàn)出來，小組學習討論時應明確分工.［1］教師采用PBL教學模式，需要創(chuàng)設一種學習情境，在情境中教學，引導學生在情境中發(fā)現(xiàn)問題，并圍繞問題獲取知識與能力，教學情境中問題應精心設置，最好具有實踐性、復雜性及層次性.（2）課堂階段.教師將課本中需要解決的問題蘊含到現(xiàn)象或事件描述中，并結合有關教學大綱及問題編制成案例資料，然后將這些案例資料按照小組形式分發(fā)給學生，組長檢查案例中是否有不懂的概念或術語，其次，進行案例解讀，并從案例中提取問題，接著提出假設，從問題出發(fā)提出問題解決的假設，將可能涉及的原因及方法、后果等提出來，第四步是確定需要增加的案例資料，第五步是最終確定學習目標，小組成員經(jīng)過商議后得出一致想要解決的問題，第六步是制定較詳細的學習計劃，分配給各小組學習任務，確定下一步學習內容及任務.［2］（3）課后自學階段.學生根據(jù)分配好的學習任務，通過查閱書籍、上網(wǎng)等方式收集資料，進行自主學習.（4）課堂總結評價階段.該階段主要是展示報告學習效果、反思并評價.

2.微課教學

微課主要是指那些以教學設計思想為基礎，利用多媒體技術在短時間內針對性講解某個知識點的視頻或者是音頻.微課在實際教學教育過程中，講授內容大多數(shù)呈現(xiàn)出“點”狀、碎片化，微課是新時期新技術的產物，是課堂教學的有效補充形式，有利于學習者進行個性化及深度化學習.教師使用微課教學形式，常常使用手機、相機或者是DV等設備進行錄制與拍攝，也可以使用有關軟件將其制作成視頻或音頻.

二、PBL模式下的高中數(shù)學微課教學實施策略分析

1.PBL模式下的高中數(shù)學微課教學實施策略陳述——以數(shù)列求和教學為例

這里以高中數(shù)學中的數(shù)列求和知識作為實例進行分析，首先，設置好要探究的課題：等差數(shù)列的前n項和，根據(jù)這一課時制定教學目標、教學重難點.然后，采用PBL教學模式：第一步設疑自探，教師在課堂教學中先創(chuàng)設一個問題情境，將17世紀莫臥兒帝國皇帝沙杰為愛妃建造的泰姬陵作為情境導入課堂，泰姬陵主要使用純白大理石砌建，是世界古建筑的七大奇跡之一，其中陵寢被寶石鑲嵌，圖案精美絕倫，陵寢是一個三角形圖案，它被大小相同的寶石鑲嵌而成，一共有100層（如圖1所示），教師這時提出問題：同學們知道這個圖案一共用了多少顆寶石嗎？

圖1

教師應使用這個情境問題引出所要講解學習的知識，吸引學生注意力，激發(fā)學生學習興趣，問題情境應采取先進多媒體手段，以微課形式展示出來，可以在正式上課前讓學生觀看有關這個建筑圖案的小視頻.［3］接著教師提問學生：看到這個問題情境，同學們能想到哪些數(shù)學問題呢？學生會就這個問題進行思考，并提出了新問題，例如，這些鑲嵌寶石有什么規(guī)律嗎？也有的想到了怎樣求1+2+3+…+100=？等差數(shù)列前n項和能使用高斯算法求解嗎？這樣教師幫助學生梳理問題，提出本課的學習目標.第二大步就是讓學生分組合作討論，小組成員先分層討論，然后再群體討論，并展示自己討論成果，明確各小組課堂任務，選派不同小組在黑板上展示問題的解決方法，通過一系列問題探討分析后，得出等差數(shù)列前n項和公式.

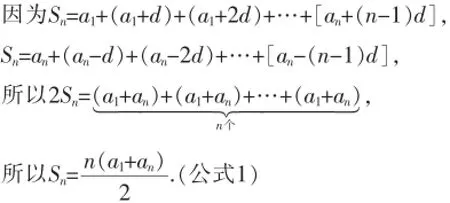
接著教師還要給學生進行有關知識補充，學生在此之前學習過an=a1+（n-1）d，因此，等差數(shù)列的另一種變形公式為

2.PBL模式下的高中數(shù)學微課教學實施策略陳述——以不等式為例

PBL教學模式以促進學生終身發(fā)展、培養(yǎng)學生創(chuàng)新能力為最終目標，因此，教師在課堂教學過程中，可以有目的、有針對性地引導學生就教師設置好的問題再提出新問題，通過改變條件、結論等形式來反復編題，培養(yǎng)學生逐漸形成良好數(shù)學思維，學生能逐漸掌握常用的數(shù)學方法解題，例如，分離常數(shù)法、配方法及數(shù)形結合法等，這里我們以高中數(shù)學中的不等式知識為例進行探討分析，將PBL模式與數(shù)學方法分離常數(shù)法應用到不等式教學及解題過程中.［4］

針對這個題目，教師向學生提出問題：這個是什么函數(shù)？如何求這個函數(shù)的最值？求值方法的靈感來源是什么？

學生會依次回答問題，并得出結果、結論：這個是分式函數(shù)，分式函數(shù)求最值要先進行變形，從而得到f（x）=示，接著教師順著學生受基本不等式啟示引導學生由等號成立，所以當x=1時，函數(shù)的最小值為9.

教師解答出答案之后，再提出這道題的變形是非常重要的，那么哪些數(shù)學題也能這樣變形呢？讓學生以小組形式進行討論，然后以微課形式在課堂上展示出來，最后進行總結得出結論.綜合上述分析及具體題目解答，能夠看出PBL模式是一種以問題促進問題的教學模式，學生只有自主探究、剖析數(shù)學知識及習題，才能提出有效問題，采取數(shù)學思維及數(shù)學方法成功解決問題.

三、結束語

PBL模式符合高中學生的認知規(guī)律及思維特征，也積極響應了新課程標準倡導的“自主”、“合作”等教學學習理念，是一種高效科學的教學方法.高中數(shù)學教師應在實際教學中就具體問題設置合理情境，引導學生提出問題，并激發(fā)學生的學習興趣與積極性，使其自主學習探究、勇于提出疑問、學會反思，從而逐漸提升自主學習能力及創(chuàng)新能力.F