“錯題”中挖潛“修正”中受益

☉山東省臨清實驗高中姚繼新

“錯題”中挖潛“修正”中受益

☉山東省臨清實驗高中姚繼新

高中數學是非常“精致”的一門學科，邏輯性強、抽象思維程度高、有嚴密的系統性，因此，不少學生談起高中數學往往是“望而生畏、敬而遠之”，平時的數學學習更是漏洞百出、顧此失彼.不僅學生如此，就是教師在命制數學試題時，有時也會因為考慮不周詳、校對不仔細等各種原因出現“錯題”.鑒于此，筆者將教學中所遇到的一些錯題進行歸類，與學生共同進行仔細推敲，既加深了同學們對數學知識的理解，增強了數學表達的規范性、準確性，同時也提高了大家思維的嚴謹性、周密性和科學性，可謂是“一舉多得”，也算是對“錯題”資源的挖掘和利用.

類型一、題目條件自相矛盾

這類問題往往是題目條件較多，彼此“牽制”，由于命題者考慮不周，忽視了各個條件之間的“兼容性”所致.

例1（2014年濰坊二模數學理10）已知定義在R上的函數y=f（x）對任意的x滿足f（x+1）=－f（x），當－1≤x＜1在［－6，+∞）上有6個零點，則實數a的取值范圍是（）.

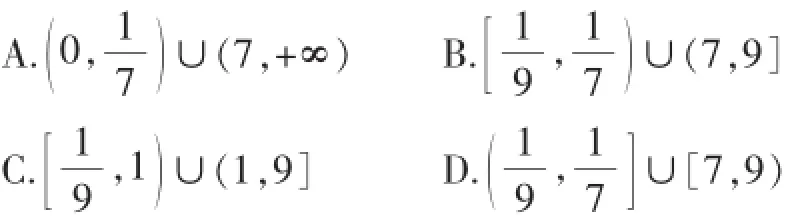
錯誤：因為定義在R上的函數y=f（x）對任意的x滿足f（x+1）=－f（x），所以令x=0，則有f（1）=0；又由當－1≤x＜1時，f（x）=x3，得f（1）=1，矛盾.

修正：“當－1≤x＜1時，f（x）=x3”應為“當－1＜x＜1時，f（x）=x3”；選項B改

例2已知偶函數y=f（x）滿足f（x+1）=－f（x），且當0≤x＜1時，f（x）=x+1，則f（x）在（1，2）上的解析式為（）.

A．f（x）=1－xB.f（x）=3－xC.f（x）=x－3D.f（x）=x－1

錯誤：因為偶函數y=f（x）滿足f（x+1）=－f（x），所以令又由當0≤x＜1時，f（x）=x+1，得

修正：去掉“偶函數”這個條件；選項B改為f（x）=－x，選B.

類型二、忽視隱含條件

這類問題往往是題設條件較多，諸多條件相互作用后有隱含性質或隱含結論產生，而這些性質或結論卻被命題人忽視所致.

例3（2005年福建高考理12）f（x）是定義在R上的以3為周期的奇函數，且f（2）=0，則方程f（x）=0在區間（0，6）內解的個數的最小值為（）.

A．2B.3C.4D.5

錯誤：因為f（x）是定義在R上的奇函數，所以f（0）= 0，進而f（3）=0；又由f（2）=0，得f（5）=0，又由f（2）=f（－1），得f（1）=f（4）=0；而且，，故方程f（x）=0在區間（0，6）內解的個數的最小值為7.

類型三、試題表述不規范

這類問題主要是表述不規范、不準確，導致在題意理解上產生歧義所致.

例4從{1，2，3，4}中隨機取一個數a，從{1，2，3}中隨機取一個數b，則事件“logba≤1”的概率是（）.

錯誤：事件“logba≤1”的表述不清楚，b=1是否可以？理解上的歧義導致答案不確定，若是b≠1，則選B；若b= 1，則選A.

修正：將事件“logba≤1”改為事件“logba≤1（b≠1）”，則選B.F