攻克一例，完解一類

☉浙江省余姚中學龔鳳

攻克一例，完解一類

☉浙江省余姚中學龔鳳

在高中平面向量的學習中，經常會遇到以三角形為載體，且涉及一串向量線性和的問題，初次接觸，使人會有無從下手的感覺.本文試圖通過對典型例題的多種解答，來揭示問題的特點和本質所在，同時找到這類問題的最佳解法.

引例△ABC的面積為12，P為△ABC所在平面內一點，且則△ABP的面積為（）.

A.3B.4C.6D.9

分析：本題的難點是如何利用所給條件來確定P點的位置，為此，可考慮用坐標法來解決.鑒于本題是選擇題，又由題意獲知，凡面積為12的三角形，只要符合條件，所得到的△ABP的面積是相等的，因此可構造特殊三角形，以簡化解題的運算過程.

解法一：如圖1，設△ABC的三個頂點為A（2，0），B（-2，0），C（0，6），又設P（x，y），則=（2-x，-y），=（-2-x，-y），2P—→C=（-2x，12-2y），3=（-12，0）.

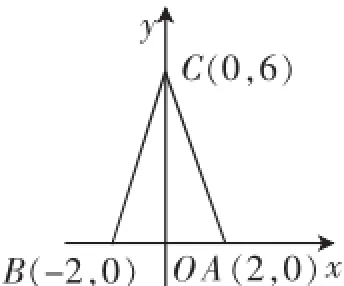
圖1

注意到P點的縱坐標為3，故可得△ABP的面積為6.

如果把本題改成證明題或解答題，解法一就不適用了，須采取如下解法.

解法二：不失一般性，如圖2，可設A（a，0），B（b，0），C（0，h），又設P（x，y），則

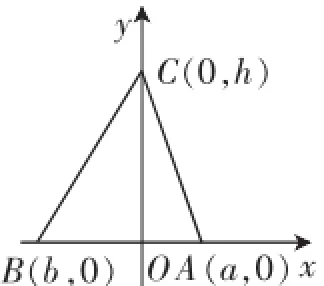
圖2

解法二較之解法一，在運算上雖麻煩了一些，但還屬于可承受的范圍；另外，讀者必須明白，當A或B是鈍角時，解法二依然是成立的.到此，讀者自然會產生這樣的一個疑問，不利用坐標法而采用向量法能否解決本題呢？回答是肯定的.

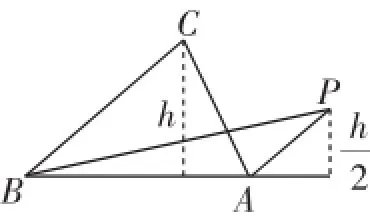
圖3

通過對上述問題的解決，不難得到兩條經驗性的結論：（1）采用坐標法解題的關鍵是坐標運算的可解性；（2）采用向量法解題的關鍵是條件等式的化簡，從中尋找向量間的關系.因此，為了獲得更佳的解法，我們需要在兩者之間做一選擇，請看下面的例題.

分析：從向量的條件等式入手去解題，似乎有較大困難，故先采用坐標法去求解.

解法一：如圖4，設A（a，0），B（b，0），C（0，h），又設P（x，y），則=（x-a，y），2=（2x-2b，2y），=（3x，3y-3h）.

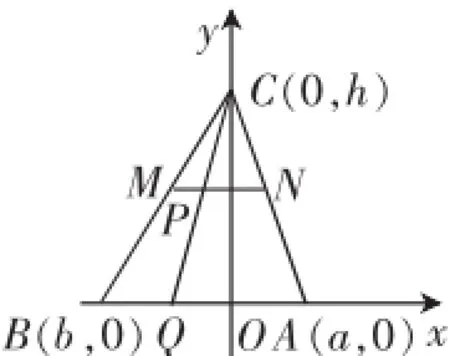
圖4

由此可知，點P在中位線MN上，此時已無需深究P點的橫坐標，立即可得C—→Q=2m.

然而，若采用向量法去求解，難度會驟然增大，不僅涉及向量的一些新知識，還要依賴于一些平面幾何的知識.

由題設知，2（P—→A+P—→B+P—

→C）=P—→A-P—

→C=C—→A，于是得到P—→G=

下面畫圖.如圖5，先畫出重心G，再畫出P點位置，CP的延長線交邊AB于點Q，PG的延長線交邊AB于點D.

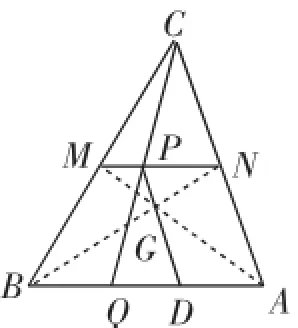
圖5

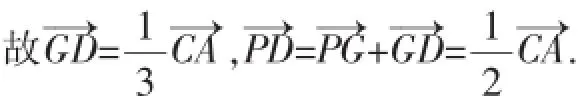
不難看出，如若變動m、n在等式中的位置或變動所求結果，并賦值予m、n，我們就能構造出許多這類問題，有興趣的讀者不妨一試.最后，必須指出，遇到此類問題，坐標法總是可行的，不過當你對條件等式的化簡確有把握時，向量法也不失是一種好方法.F