股市收益率高階矩風險的產生機制檢驗

方立兵，曾 勇

(1. 南京大學工程管理學院，江蘇 南京 210093；2. 電子科技大學經濟與管理學院， 四川 成都 611731)

?

股市收益率高階矩風險的產生機制檢驗

方立兵1，曾 勇2

(1. 南京大學工程管理學院，江蘇 南京 210093；2. 電子科技大學經濟與管理學院， 四川 成都 611731)

通過對現有理論文獻的梳理，提煉了五個較為典型的關于高階矩風險產生機制的理論假設。然后基于時變高階矩建模思想，將這五個假設統一于同一個計量框架，并進行綜合地實證檢驗，以期發掘具有“占優”作用的理論解釋。以滬深股市收益率為樣本研究發現，在這五個假設中，僅“波動率反饋”效應和“利空信息揭示”效應獲得顯著的實證支持。進一步分析指出，這兩種效應會同時引起偏度和峰度風險，因而是高階矩風險的主要產生機制。這一結果可為后續研究發展一個統一的理論框架提供實證參考。

高階矩風險；波動率反饋；限制賣空；條件密度

1 引言

近年來，高階矩風險在金融理論和實踐領域扮演著越來越重要的角色。然而，就在學術界和實務界對高階矩風險的重要性逐漸達成共識的同時，關于高階矩風險的產生機制卻一直眾說紛紜、各有側重。就偏度風險的產生機制而言，早期比較有代表性的觀點是Pindyck[1]、French等[2]以及Campbell和Hentschel[3]討論的“波動率反饋”效應，即信息沖擊會放大投資者的風險預期，從而提高風險補償，結果削弱了好消息對價格的“拉升”作用，而放大了壞消息對價格的“打壓”作用，從而引起收益率分布負偏。近期的觀點如Hong和Stein[4](下稱“HS模型”)認為，賣空限制使得悲觀投資者的利空信息難以立即揭示而逐漸累積，此后與新的利空信息同時揭示的可能性增加，即易于發生利空信息“雪崩”。但利好信息通常可以得到立即揭示，因為至少從交易機制來看，并不存在買入限制的制度約束。這就預示著，即便影響程度相同的利好和利空信息等可能到達，限制賣空的交易機制也會增加市場發生大幅下跌的機率，引起負偏風險。Xu[5]進一步引入有限理性的行為偏差，并指出(下稱“Xu模型”)，在賣空限制的作用下，市場對好消息容易出現過度反應，而對壞消息容易反應不足，后續的價格修正會將偏度“推”向相反方向，從而引起負偏。

就峰度風險的產生機制而言，早期比較有代表性觀點認為收益率的峰度風險源自波動過程的“聚集性(Clustering)”。Engle[6]提出的ARCH模型以及Bollerslev[7]發展的GARCH模型均可在理論上證明，即便收益率為條件正態分布(信息沖擊是依正態過程到達)，波動過程的(G)ARCH性質仍然預示著市場的收益率存在峰度風險。

Romer[8](下稱“Ro模型”)從信息的角度給出了峰度風險的另一個解釋：市場上每個投資者僅擁有很少的一部分有價值的信息，即信息不完全且非常分散，其結果是市場難以在短期內充分揭示所有信息，并導致部分信息因此而開始累積。隨著新信息的陸續到達并逐漸累積，投資者掌握的有價值的信息越來越多，從而導致所有信息一并揭示的可能性逐漸增加，引起峰度風險。

Abreu和Brunnermeier[9]基于投資者行為視角提出了新的觀點(下稱“AB模型”)。他們認為，投資者的有限理性行為(動量交易、趨勢追蹤等)使得市場對過去的信息存在非理性反應，從而引起價格出現大幅漲跌。更為重要的是，即便理性的套利者知道這個情況，他們仍然會順勢而為，以獲取高額回報，而不是反向操作，修正定價偏誤。這就預示著即便引起市場大漲和大跌的外生信息服從正態分布，投資者上述交易行為也會內生地引起股市頻繁出現大幅上漲和下跌，從而產生峰度風險。

對于上述理論解釋，相關的實證研究往往只針對其中的部分解釋進行檢驗。例如Campbell和Hentschel[3]檢驗了波動率反饋效應并指出，波動率反饋效應僅在市場處于高波動期間對收益率產生顯著影響。此后，陸續有經驗證據涉及波動率反饋效應，但結論不盡一致[10-13]。Engle和Mistry[14]指出市場指數作為定價因子與“波動率反饋”效應是一致的。Kinnunen[15]則指出市場指數收益率的“波動率反饋”效應的存在性隨著信息流到達水平的變化而不斷變化。Hueng和McDonald[16]以及Hueng[17]采用自回歸條件密度建模方法，分別以美國和中國股市收益率為樣本檢驗了HS模型“利空信息揭示”效應，結果發現僅在中國股市顯著存在。陳國進和張貽軍[18]運用固定效應條件Logit模型給出證據支持 “利空信息揭示”效應。Xu Jianguo[5]利用美國股市的數據為其理論模型給出了支持性的證據。

縱觀現有研究可以發現，相關理論文獻對高階矩風險產生機制的解釋各有側重，而實證文獻則大多針對其中的一到兩種解釋進行檢驗，故而容易導致“各自為政”的局面，最終難以較為確切地回答高階矩風險究竟是怎樣產生的，哪些產生機制具有“占優”作用，或者說，哪些產生機制在考慮了其他機制后仍然顯著存在，而哪些產生機制在考慮了其他機制后不再顯著？值得說明的是，波動率反饋效應屬于同質信念模型框架，反映了“加總的(Aggregated)”風險厭惡行為，而HS模型、Xu模型、Ro模型和AB模型等屬于異質信念模型，著眼于分析不同信念投資者的交易行為以及由此產生的價格發現過程。可見，這些機制解釋往往源自不同的理論框架。鑒于此，本文將上述解釋統一于同一個計量框架，從而檢驗并識別哪些機制具有“占優”作用。

本文借鑒Hansen[19]提出的自回歸條件密度建模思想，構建時變的高階矩模型，進而對上述理論解釋進行綜合地計量檢驗。以1998年1月1日至2011年5月31日滬深兩市指數收益為樣本，在控制了“周內效應”和“假日效應”后(更為保守地獲得較高的檢驗勢)，研究發現，相關理論解釋中，僅“波動率反饋”效應和“利空信息揭示”效應顯著存在。雖然這兩種效應主要用于解釋收益率負偏風險的產生機制，但進一步分析可以發現，“利空信息揭示”效應常常伴隨著較大的左尾風險，這實際上也是屬于峰度風險的范疇。另外，與“波動率反饋”效應相應的波動“聚集性”和“持續性”也可以解釋峰度風險的產生。因此，本文認為“波動率反饋”效應(包括波動過程的“聚集性”和“持續性”)和“利空信息揭示”效應是股市收益率高階矩風險的主要產生機制。

2 相關假設的提出

根據現有研究給出的理論解釋，除了波動聚集性是收益率的“典型事實”之外，對于高階矩風險的產生機制，我們可以提煉出如下五個可供實證檢驗的理論預示。首先，波動率反饋效應描述的是預期波動與預期收益之間的關系，即：

假設1：條件波動與預期收益正相關。

正是這種“波動-收益”的正相關關系造成了好消息的沖擊作用被削弱而壞消息的沖擊作用被放大。在對異質信念模型的理論預示進行實證檢驗時，以Hong和Stein[4]、Chen等[20]、陳國進和張貽軍[18]等為代表的一系列文獻建議，以交易量作為信念差異程度的代理變量。HS模型的“利空信息揭示”效應指出，投資者的信念差異程度越大，交易量越大。相應的，負偏風險越嚴重。因此，HS模型和Ro模型分別預示著：

假設2：條件偏度與前期的交易量負相關。

假設3：條件峰度與前期的交易量正相關。

Xu模型和AB模型描述的都是投資者對前期收益的過度反應行為，以及后期的價格修正與收益率高階矩風險的關系。這兩個模型預示：

假設4：條件偏度與前期的收益負相關。

假設5：條件峰度與前期收益的絕對值正相關。

3 模型方法

3.1 波動聚集與波動率反饋

描述收益率波動聚集性的標準手段是GARCH族模型框架。但為了引入“波動率反饋”效應，考慮如下模型：

rt=μt+vht+εtεt～IID(0,ht)

(1)

其中，rt表示收益率，ht=Var[rt|Ωt-1]，Var[·|Ωt-1]表示條件方差運算；Ωt-1表示t-1期及以前的信息集；μt+vht構成rt的條件均值；εt是新生量(Innovation)，刻畫的是第t期的信息沖擊。均值方程中的系數v描述了期望收益與波動之間的關系。假設1預示v>0。為刻畫收益率波動聚集性的同時，引入波動過程的杠桿效應，選擇結構簡潔、意義明確的GJRGARCH[10]模型描述條件波動ht的動態過程：

(2)

其中，系數ω是常數項，α和θ分別描述了新信息εt對預期波動的沖擊和非對稱沖擊；I{·}是示性函數，即當括號中的條件成立時取1，否則取0。聯合(1)和(2)式即為GJRGARCH-m模型。在此模型中，波動過程的持續性預示α+β是一個接近于1的正數；波動聚集性要求α>0時；杠桿效應要求γ>0。

3.2 時變高階矩建模與假設2～4

假設2～4的實證檢驗均需要刻畫收益率的時變高階矩(偏度和峰度)與過去的信息(收益率和成交量)之間的關系。因此，借鑒Hansen[19]提出的Skew-T分布：

(3)

其中，λ和η分別是偏度系數和自由度；sgn(·)是符號函數；A、B和C都是λ和η的函數；λ>0和λ<0分別表示概率分布為正偏和負偏，而且|λ|越大，偏度越高，η越小，“峰”越“尖”，“尾”越“厚”，價格發生大幅跳躍的可能性越高，峰度越大，反之亦反之。因此，Skew-T分布可以較好地反映收益率的高階矩風險。λ和η分別稱為“偏態參數”和“峰態參數”，或統稱為“形態參數”。

借鑒Hansen[19]的自回歸條件密度建模思想，假定(3)式中的偏度系數和自由度具有時變性，并重新記為λt和ηt：

(4)

(5)

(4)和(5)式分別描述了收益率的偏度系數和自由度的動態過程。這里分別稱其為“偏態方程”和“峰態方程”，或統稱為“形態方程”。其中，ai和bi分別是偏態方程和峰態方程中各項的系數，i=0,1,2,3,4；g(l,u)(x)是Logistic轉換函數，用以將x映射到區間(l,u)中，以得到合理的結果。根據SkewT的定義，-1<λt<1；ηt>3是為了確保概率分布的偏度是有限的；ηt<30是因為自由度超過30的學生t分布與正態分布具有類似的尾部。(4)和(5)式中的a1和b1分別刻畫了偏態系數(λt)和峰態系數(ηt)與前期收益率之間的關系，而a4和b4則分別刻畫了λt和ηt與前期交易量之間的關系。

3.3 控制“周內效應”和“假日效應”

“周內效應”和“假日效應”是市場中兩種常見的收益率“異象”，有時也被稱為“日歷效應”。“周內效應”指的是星期一至星期五中某個交易日，如星期一(星期五)的收益率常常顯著高于(低于)星期內的其它交易日；“假日效應”指的是收益率在長假前后的交易日常常具有顯著較高或較低的收益率。鑒于此，均值方程中的μt設為：

(6)

其中，μ是常數項，vτ是自回歸系數，滯后階數為p(由信息準則確定)，MONt、TUEt、WEDt和THUt分別是星期一到星期四的虛擬變量；BHt和PHt分別是節假日的后一個交易日和前一個交易日的虛擬變量；節假日包括元旦節、春節、清明節、勞動節等“小長假”或“黃金周”。

3.4 模型參數的估計

對應假設2預示收益率的偏態系數與過去的交易量負相關(a4<0)；假設3預示峰態系數與過去交易量負相關(b4<0)；假設4預示偏態系數與過去信息沖擊負相關(a1<0)；假設5預示峰態系數與過去的信息沖擊的絕對值負相關(b1<0)。

4 樣本描述及一些初步的結果

本文以滬深兩市綜合指數1998年1月1日至2011年5月31日的對數百分比收益為樣本(樣本量T=3239)，對假設1～5進行實證檢驗。雖然我國滬深兩市于2010年3月31日啟動了融資融券試點，但在本文的樣本期內，標的股票數量很少。更為重要的是，融券券源的缺乏使得我國的融券業務(在兩融業務中的占比不足10%)一直遠低于融資業務。因此，我們認為融資融券的推出并不會改變限制賣空的假設。正如Hong和Stein(2003)[4]所指出的，即便是美國的股票市場，賣空交易的實務中也是存在諸多約束的，其賣空機制也不是真正意義上的賣空。因此，HS模型的理論預示并不要求市場是禁止賣空的，在限制賣空的機制下HS模型仍然是適用的。表1給出了原始收益率以及標準化收益率的描述性統計結果。

表1 滬深兩市指數收益率的描述性統計

注：(1)標準化收益率是指原始收益率經正態分布假設下的GJRGARCH-m模型擬合后的標準化殘差；(2)在正態分布的假設下，樣本的偏度和峰度分別依分布收斂于N(0,6/T)和N(3,24/T)，其中T為樣本量；(3)Q(q%)表示樣本在q%水平上的經驗分位數；(4)圓括號中的數值為相應統計量p-值；(5)以粗體顯示的數值表示其p-值小于顯著性水平10%。若未做特殊說明，下同。

表2 正態分布假設下GJRGARCH-m模型的極大似然估計

從表1可以看出，上證指數和深證綜指的原始收益率均存在顯著的負偏風險。從位置參數來看，兩市指數的原始收益率和標準化收益率的均值都小于中位數，即存在負偏風險。此外，表1還顯示，原始收益率和標準化收益率均存在顯著的超額峰度。上證指數的標準化收益率未見顯著的偏度風險，而深證綜指的標準化收益率顯著負偏。

最后，Jarque-Bera統計量顯示兩市指數的原始收益率和標準化收益率均存在顯著的高階矩。另外，從95%和5%、85%和15%以及75%和25%水平上的經驗分位數來看，兩市標準化收益率均可能存在非對稱風險，且左尾風險相對較大，如兩市指數的原始收益率和標準化收益率樣本的95%分位數均小于5%分位數的絕對值。

表2給出了正態分布假設下GARCH-m模型的參數估計結果。從均值方程可以看出，兩市指數收益率均存在顯著的“周內效應”和“假日效應”，這與國內現有的相關研究是類似的。方差方程估計結果顯示，兩市指數收益率的波動過程均存在高度的持續性和波動聚集現象。γ顯著為正說明負向沖擊引起的收益率波動更大。ht顯著為正，即均值方程中的預期收益率與波動存在顯著的正相關關系。可以認為收益率序列存在顯著的“波動率反饋”效應。

另外，與其他研究類似，本文也將以交易量作為投資者信念差異程度的代理變量。但需要剔除交易量的時間趨勢和印花稅的影響。考慮如下回歸：

(7)

5 實證結果

5.1 檢驗假設1

實際上，表2給出的正態分布假設下有關收益率波動過程的參數估計結果已經初步支持了假設1。下面進一步在Skew-T分布的假設下估計GJRGARC-m模型，但先假設條件分布形態不隨時間發生改變，即λ和η均為常數。結果如表3所示。限于篇幅，且其它系數的估計結果與表2類似，這里僅給出本文關注的系數估計結果。

比較表2和表3可以看出，就“波動率反饋”效應來講，正態分布的GJRGARCH-m模型的估計結果與Skew-T分布假設下的估計結果是類似的。表3的結果也顯示，α+β平均約為0.9575，即波動過程具有高度的持續性；預期波動與預期收益率存在顯著的正相關關系(v>0)。因此，可以認為兩市指數的收益率序列存在顯著的“波動率反饋”效應，支持了假設1。負向沖擊引起的收益率波動顯著高于正向沖擊，即波動過程表現出顯著的非對稱性。表3給出的似然比檢驗結果表明，Skew-T分布的擬合優度顯著高于正態分布。從分布函數的偏態參數和峰態參數的估計結果來看，兩市標準化收益率依然存在顯著的負偏度和尖峰、厚尾性(自由度遠小于30)。

表3 Skew-T分布假設下GJRGARCH-m模型的極大似然估計

注：(1)均值方程和方差方程依然沿用表2的設定；(2)圓括號中的數值為相應統計量的p-值；(3)以粗體顯示的數值表示其p-值小于顯著性水平10%。若不做特殊說明，下同。

事實上，表3給出的結果是在收益率的條件分布形態(Skew-T分布的偏態系數和峰態系數)不隨時間發生改變的假設下得出的。這相當于對(4)和(5)式施加如下約束：

a1=a2=a3=a4=b1=b2=b3=b4=0

(8)

接下來將對上述約束采用逐個放松的方法，確定收益率的條件高階矩的動態過程，從而實現對假設2～5的檢驗。基于似然比檢驗對不同偏態方程和峰態方程設定下的擬合優度進行比較。

5.2 檢驗假設2和假設4

要檢驗假設2和假設4，需要事先確定偏態方程的結構。為此，先假定條件分布的峰態參數(η)為一個常數，即對峰態方程(5)式施加如下約束b1=b2=b3=b4=0。然后，考慮(4)式在約束a1=a2=a3=a4=0的基礎上分別逐步放松a1=0、a2=0、a3=0和a4=0等約束條件的參數估計結果。表4給出了放松a1=0的估計結果。限于篇幅，這里僅給出本文關注的系數估計結果。

從表4可以看出，當偏態系數隨時間改變時，預期收益與波動的關系以及波動過程的非對稱性、持續性特征沒有發生改變。比較表2和表3可以發現，系數v、γ以α+β的估計值也相似，即收益率序列的“波動率反饋”效應和峰度風險顯著存在。

對于這里關心的λt與前期的信息沖擊εt-1之間的關系，估計結果并非顯著異于0，即假設4并未得到支持。且似然比檢驗的結果也顯示表4所對應的模型并非由于表3的模型。

下面考慮逐個放松約束a2=0、a3=0和a4=0的情形(限于篇幅，具體結果從略)。從估計結果來看，兩市指數收益率的條件偏度都與過去的負向信息沖擊(I(εt-1<0)εt-1)和交易量(TVt-1)顯著正相關和負相關，即a2>0，a4<0。似然比檢驗也顯著拒絕了a2=0和a4=0。這說明本文的假設2在這里得到支持。對于假設4來說，這里不僅沒有給出支持性的證據，a2>0甚至意味著，如果前期存在負向沖擊，則當期收益率將更加易于發生負偏風險。由于逐個放松約束的結果顯示，僅a2和a4顯著異于0。因此，考慮對(4)式施加約束a1=a3=0并進行極大似然估計，結果再次支持了假設2。另外，與逐個放松約束的結果類似，收益率的條件偏度與前期的負向信息沖擊(I(εt-1<0)εt-1)正相關。且似然比檢驗結果顯示a1=a3=0約束下的模型優于a1=a2=a3=a4=0。因此，偏態方程(4)式將被設定為如下形式：

(9)

5.3 檢驗假設3和假設5

采用與5.2節類似的方法確定確定峰態方程的形式(具體數據從略)。結果顯示，除了系數b1、b2和b4的符號與假設3和假設5的預示一致之外，從p-值來看，這些系數均未顯著異于0。這說明收益率的峰態特征(ηt)與過去的信息沖擊(εt-1)和交易量(TVt-1)并無顯著的相關關系。因此，假設3和假設5所對應的理論預示都沒有獲得顯著的實證支持。另外，就模型的擬合優度來講，似然比檢驗的結果也顯示，放松bi=0(i=1,2,3,4)中的任何一個約束條件都難以改進模型的擬合優度。進一步考慮將偏態方程設定為5.2節給出的(9)式，并分別在各種約束條件下，再次進行極大似然估計，結果如表5所示。

表4 η為常數且(4)式在a2=a3=a4=0約束下模型的極大似然估計

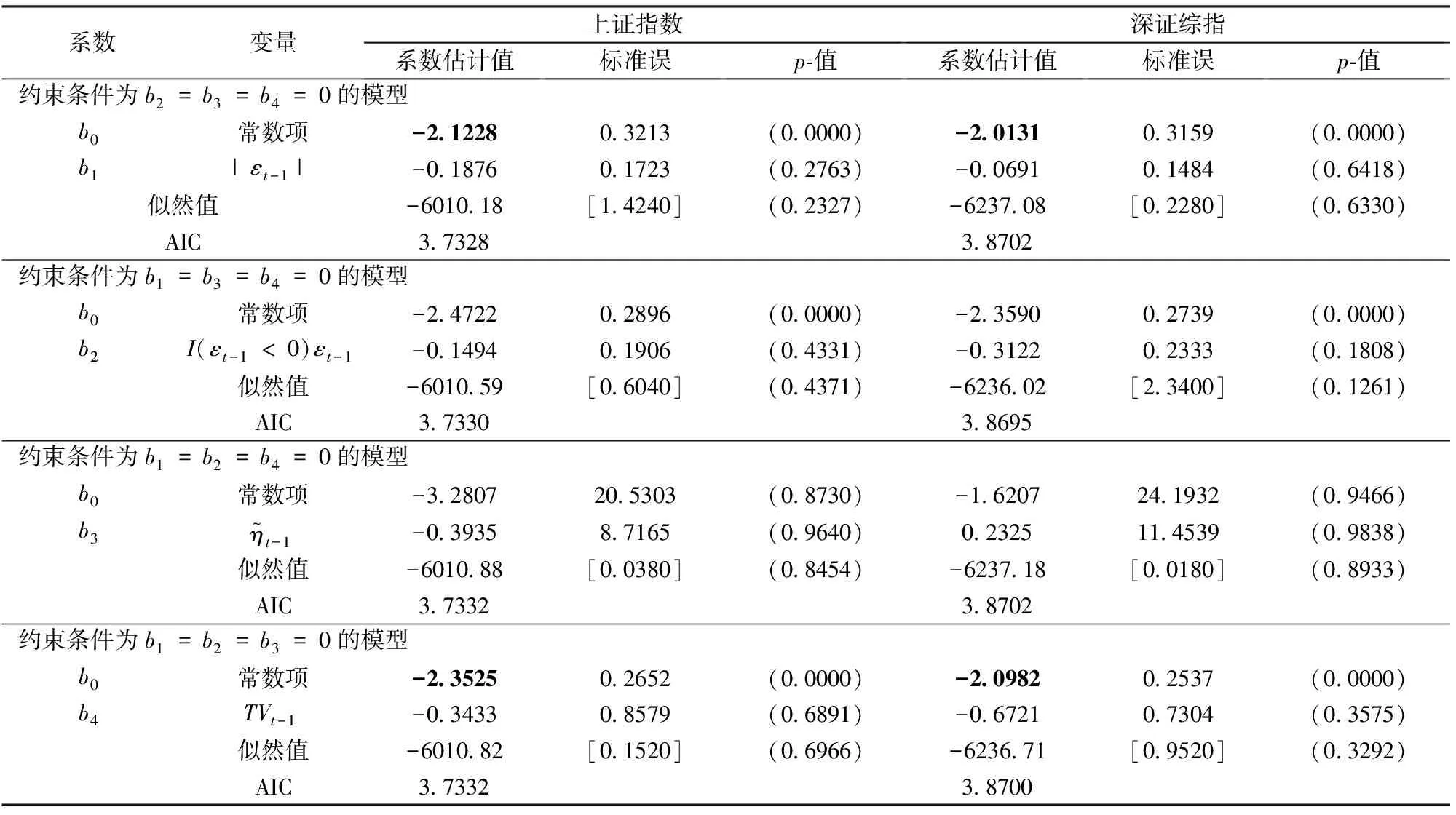
表5 偏態方程為(9)式且(5)式在各種約束條件下的極大似然估計

從表5可以看出，假設3和假設5所對應的理論預示在這里仍然難以得到實證支持，即系數b1、b2和b4均非顯著異于0的。另外，所有的似然比檢驗均沒有顯著拒絕bi=0(i=1,2,3,4)。因此，就模型的擬合優度來講，當偏態方程設定為(9)式和常數的結果類似，即放松bi=0(i=1,2,3,4)的任一約束都難以獲得更好的擬合優度。

5.4 實證結果的進一步分析

雖然本文對假設1～5的統計檢驗是分開進行的，但這些理論預示所反映的高階矩風險的產生機制彼此也有一定的聯系。“波動率反饋”效應和“利空信息揭示”效應預示的資產價格易于發生大幅下跌，意味著收益率的左尾風險相對較大。這實際上也屬于峰度風險的范疇。因此，這兩種效應的影響結果不僅僅是產生偏度風險，同時也會導致峰度風險。以Skew-T分布為例，其標準化四階中心矩(峰度)Kur(z)為：

Kur(z)=(m4-4Am3+6A2m2-3A4)/B4

圖1 Skew-T分布的偏態系數與理論峰度：以上證指數的估計結果為例

另外，從圖1(b)還可以看出這樣兩個現象：一是在“利空信息揭示”效應的影響下，收益率的偏態系數λt大多是小于0的，即收益率易于產生負偏風險；二是當收益率正偏時，λt的取值不會超過0.1，而當負偏發生時，λt最高可以達到-0.3200，即市場易于產生較為嚴重的負偏風險。因此，在“利空信息揭示”效應的影響下，收益率的高階矩特征會出現如下三個方面的結果：(1)市場產生負偏風險的可能性高于正偏；(2)負偏風險往往比正偏風險更加嚴重；(3)偏度風險產生時會伴隨峰度風險。

最后，收益率的峰度風險常常與波動過程的聚集性、非對稱性和持續性等“典型事實”(StylizedFacts)聯系在一起。本文所有模型的擬合結果也都顯示，這些典型事實是顯著存在的。從表2的描述性統計結果來看，滬深兩市指數的原始收益率和標準化收益率之間的峰度差異分別約為1.4107和1.2571。也就是說，收益率的波動過程表現出的典型事實也可以部分地解釋峰度風險。

6 與國際成熟市場的比較

我們進一步采集了美國SP500指數和英國FTSE100指數的收益率和交易量數據(數據來自Wind金融資訊終端)，重新檢驗了本文的五個假設。但結果發現(限于篇幅，具體的數據結果這里從略，但我們歡迎感興趣的讀者來信索取。)，與我們采用國內滬深指數的結果存在顯著差異：兩個成熟市場的“波動率反饋”效應(假設1)和“利空信息揭示”效應(假設2)沒有得到證據支持，而假設3(Ro模型)和假設5(AB模型)卻是得到支持的。

綜合成熟市場的結果，我們可以看出國際成熟市場的高階矩風險產生機制可能不同于我國股市。事實上，Hueng和McDonald[16]和Hueng[17]就曾分別對美國和中國股市的“利空信息揭示”效應進行了檢驗，并且也發現美國股市并無顯著的“利空信息揭示”效應，而中國股市卻顯著存在。此外，對于本文所提出的五個待檢驗的假設，SP500指數和FTSE100指數高階矩風險中，Ro模型和AB模型的理論預示具有占優作用。這與本文基于中國股市為樣本得出的結論也明顯不同。直觀上來講，不同市場在投資者行為特征、交易機制設計等諸多方面往往都是存在顯著差異的，而成熟市場和新興市場之間的差異往往會更大，例如美國股市的賣空限制程度顯然弱于國內市場。這一點從兩個市場的賣空交易活躍性便可見一斑。美國股市中20%以上交易量由賣空者發起[21]，而我國股市中，融券賣空的交易額在兩融業務中的占比都不到10%，相對于整個市場的交易量而言，則少于1%。更重要的是，在本文的樣本中，1998年1月至2010年3月這段時間里我國股市甚至是禁止賣空的。因此，本文基于國內股市所得到的結果與國際市場的結果存在顯著差異也就是顯然的了。

7 結語

股市收益率高階矩風險的重要性已經得到普遍認同，但對于其產生機制的解釋，依然眾說紛紜。本文在對相關研究提出的理論解釋進行較為系統地梳理后，提煉了五個可供實證檢驗的假設；然后，以中國滬深兩市的指數收益為樣本，采用自回歸條件密度的建模思想，將這五個假設統一于同一個計量框架，進而考察高階矩風險的產生機制，以及哪些產生機制具有“占優”作用？為了使得檢驗的結果較為可靠，模型還控制了收益率可能存在的“周內效應”和“假日效應”等收益率“異象”。

研究結果表明，這五個理論預示中，僅“波動率反饋”效應(假設1)和“利空信息揭示”效應(假設2)顯著存在。除此之外，未發現顯著的證據支持其它的三個理論預示。需要說明的是，雖然“波動率反饋”效應和“利空信息揭示”效應主要用于解釋市場收益率的偏度風險，但進一步分析可以發現，“利空信息揭示”效應在引起偏度風險的同時，也會引起峰度風險，而“波動率反饋”效應中與波動過程相關的“聚集性”和“持續性”等典型事實(StylizedFacts)也是峰度風險的重要產生機制。因此，可以認為，“波動率反饋”效應(包括其中的波動“聚集性”和“持續性”)與“利空信息揭示”效應是股市收益率高階矩風險的主要產生機制。

作為比較，我們還以美國的SP500指數和英國的FTSE100指數為樣本對本文提出的五個假設進行了檢驗，但并未發現與滬深指數一致的證據。進一步分析后，我們認為不同市場在投資者行為特征、交易機制設計等諸多方面往往存在較大差異，在這樣的背景下，不同市場的高階矩風險具有不同的產生機制也是可能的。特別的，新興市場和成熟市場的高階矩風險的產生機制往往具有各自不同的特點。

雖然如此，本文以我國滬深指數為樣本，通過構建一個統一的計量框架，從眾多高階矩風險產生機制的解釋中，經驗性地識別出具有“占優”作用的兩種解釋——“波動率反饋”效應和“利空信息揭示”效應。這至少為進一步深入探求我國股市高階矩風險的產生機制理出了頭緒，也為構建一個統一的理論框架提出了可供參考的研究方向。例如，將“波動率反饋”效應引入限制賣空(現實的股市總是限制賣空的)的異質信念模型(HS模型)，沿著價格發現過程存在“利空信息揭示”效應邏輯主線，構建一個統一的理論框架，以期為充分揭示股市收益率高階矩風險的產生機制，提供新的理論解釋。當然，最終目的是為了發展一個較為完備的理論框架，突破現有的理論模型各有側重的不利局面。

[1]PindyckRS.Risk,inflation,andthestockmarket[J].AmericanEconomicReview, 1984, 74(3): 335-351.

[2]FrenchKR,SchwertGW,StambaughRF.Expectedstockreturnsandvolatility[J].JournalofFinancialEconomics, 1987, 19(1): 3-29.

[3]CampbellJY,HentschelL.Nonewsisgoodnews:Anasymmetricmodelofchangingvolatilityinstockreturns[J].JournalofFinancialEconomics, 1992, 31(3): 281-318.

[4]HongH,SteinJC.Differencesofopinion,short-salesconstraints,andmarketcrashes[J].ReviewofFinancialStudies, 2003, 16(2): 487-525.

[5]XuJianguo.Priceconvexityandskewness[J].JournalofFinance, 2007, 62(5): 2521-2552.

[6]EngleRF.AutoregressiveconditionalheteroscedasticitywithestimatesofthevarianceofUnitedKingdominflation[J].Econometrica, 1982, 50(4): 987-1007.

[7]BollerslevT.Generalizedautoregressiveconditionalheteroskedasticity[J].JournalofEconometrics, 1986, 31(3): 307-327.

[8]RomerD.Rationalasset-pricemovementswithoutnews[J].AmericanEconomicReview, 1993, 83(5): 1112-1130.

[9]AbreuD,BrunnermeierMK.Bubblesandcrashes[J].Econometrica, 2003, 71(1): 173-204.

[10]GlostenLR,JagannathanR,RunkleDE.Ontherelationbetweentheexpectedvalueandthevolatilityofthenominalexcessreturnonstocks[J].JournalofFinance, 1993, 48(5): 1779-1801.

[11] 王春. 投資者情緒對股票市場收益和波動的影響——基于開放式股票型基金資金凈流入的實證研究. 中國管理科學, 2014, 22(9): 49-56.

[12]BrandtMW,WangLeping.Measuringthetime-varyingrisk-returnrelationfromthecross-sectionofequityreturns[R].Workingpaper,DukeUniversty, 2010.

[13]YuJianfeng,YuanYu.Investorsentimentandthemean-variancerelation[J].JournalofFinancialEconomics, 2011, 100(2): 367-381.

[14]EngleR,MistryA.Pricedriskandasymmetricvolatilityinthecrosssectionofskewness[J].JournalofEconometrics, 2014, 182(1): 135-144.

[15]KinnunenJ.Risk-returntrade-offandserialcorrelation:Dovolumeandvolatilitymatter?[J].JournalofFinancialMarkets, 2014, 20: 1-19.

[16]HuengCJ,McDonaldJB.Forecastingasymmetriesinaggregatestockmarketreturns:Evidencefromconditionalskewness[J].JournalofEmpiricalFinance, 2005, 12(5): 666-685.

[17]HuengCJ.Short-salesconstraintsandstockreturnasymmetry:evidencefromtheChinesestockmarkets[J].AppliedFinancialEconomics, 2006, 16(10): 707-716.

[18] 陳國進, 張貽軍. 異質信念、賣空限制與我國股市的暴跌現象研究[J]. 金融研究, 2009, (4): 80-91.

[19]HansenBE.Autoregressiveconditionaldensityestimation[J].InternationalEconomicReview, 1994, 35(3): 705-730.

[20]ChenJ,HongH,SteinJC.Forecastingcrashes:Tradingvolume,pastreturns,andconditionalskewnessinstockprices[J].JournalofFinancialEconomics, 2001, 31(3): 345-381.

[21]BoehmerE,WuJuan.Shortsellingandthepricediscoveryprocess[J].ReviewofFinancialStudies, 2013, 26(2): 287-322.

TestingtheGenerationMechanismofHigher-Order-MomentRiskinStockMarketReturns

FANG Li-bing1, ZENG Yong2

(1. School of Management and Engineering, Nanjing University, Nanjing 210093,China; 2. School of Management and Economics,University of Electronic Science and Techonology of China, Chengdu 611731,China)

Five pieces of theoretical prediction on the generation of higher order moment risk are refined and thus the corresponding hypotheses are formed after reviewing the existed literature. Employing the idea of modeling time variant higher-order-moment, these five pieces of hypothesis are involved in a unified econometric framework. An empirical analysis is conducted based on such model to find some dominated theoretical explanations. Sampling daily returns from Shanghai and Shenzhen stock market composite index, the results show that there are two hypotheses relevant to volatility feedback effect and bad news revelation effect are significantly supported but the other three are not. Further analysis indicates that these two effects can generate both skewness and kurtosis risk. Therefore, they are implied as the main generation mechanism of higher-order-moment risk. These results get out of the mess of opinions on the generation mechanism of higher-order-moment risk and thus can benefit further exploration of such topic under a unified theoretical framework.

higher-moment risk; volatility feedback; short-sale constraint; conditional density

1003-207(2016)04-0027-10

10.16381/j.cnki.issn1003-207x.2016.04.004

2014-10-19；

2016-01-09

國家自然科學基金青年資助項目(71401071)；教育部人文社會科學研究青年資助項目(14YJC790025)；江蘇省自然科學基金青年資助項目(BK20130589)

方立兵(1980-)，男(漢族)，安徽舒城人，南京大學工程管理學院講師，研究方向：金融市場計量與金融工程研究，E-mail:lbfang@nju.edu.cn.

F830.91

A