不公平厭惡下VMI供應鏈的批發價格契約與協調

劉云志，樊治平

(東北大學工商管理學院，沈陽 110169)

?

不公平厭惡下VMI供應鏈的批發價格契約與協調

劉云志，樊治平

(東北大學工商管理學院，沈陽 110169)

供應鏈契約是影響VMI供應鏈整體績效的重要因素，這是近年來關注的重要研究課題。本文著重研究了由供應商與零售商組成的二級VMI供應鏈協調問題，在供應商存在不公平厭惡的假設下，依據Cui等提出的不公平厭惡模型刻畫了供應商的不利與有利不公平厭惡，通過分析得到了分散VMI供應鏈情形下供應商的最優策略，同時分析了二級VMI供應鏈在批發價格契約下的協調情況。通過分析得到的主要結論是：在供應商存在不利不公平厭惡的情形下，供應商存在唯一的最優產品生產量，其不高于傳統供應商的最優產品生產量且為不利不公平厭惡系數或零售商勢力外生參數的嚴格減函數或減函數，批發價格契約無法使二級VMI供應鏈達到協調；在供應商存在有利不公平厭惡的情形下，供應商存在唯一的最優產品生產量，其不低于傳統供應商的最優產品生產量且為有利不公平厭惡系數或零售商勢力外生參數的嚴格增函數或增函數，批發價格契約在一定條件下可使二級VMI供應鏈達到協調。最后，通過數值實驗分析驗證了本文得出的結論。

VMI；供應鏈協調；不公平厭惡；批發價格契約

1 引言

供應商管理庫存(VMI,Vendor Managed Inventory)是一種供應鏈戰略，其是指上級供應方管理下級訂貨方的庫存。從廣義上來說，VMI可以在供應鏈上的任何兩個節點之間實現，并使得供應方能夠監視訂貨方的庫存水平，并承擔必須的庫存補給責任，確保一定的庫存周轉目標和顧客服務水平，增強供應鏈的運作效率[1]。由于VMI作為一種集成化的庫存管理方法，能夠促進信息分享、降低牛鞭效應和提高供應鏈協作水平[2]，所以其受到了許多學者的關注[3-5]。通常，通過VMI不能使供應鏈達到協調，即不能消除雙重邊際化效應對供應鏈所帶來的負面影響，而供應鏈契約是實現供應鏈協調的主要方法，通過合理的契約設計以及相應的參數設置，有助于消除雙重邊際化效應、提高供應鏈的整體利潤，從而使供應鏈達到協調[6]。供應鏈契約主要包括批發價格契約、回購契約、收益共享契約、數量折扣契約等，其中批發價格契約作為供應鏈契約中形式最為簡單的契約，因其執行起來較為便捷且管理成本較低，故在現實中被廣泛采用。因此，近年來針對VMI模式下供應鏈的批發價格契約與協調的研究越來越受到學術界的關注[7-9]。目前，可以看到一些學者針對VMI模式下供應鏈的批發價格契約與協調的研究成果[7-9]，例如，Gerchak和Wang[7]針對由多個供應商與單一零售商(裝配商)組成的二級供應鏈協調問題，研究了VMI模式下二級供應鏈在收益共享與批發價格契約下的協調情況，并指出在雙參數契約下供應鏈可達到協調，且有利于供應鏈成員利潤的增加，VMI模式下供應鏈在單一收益共享契約下的運作效率要優于在單一批發價格契約下的運作效率；唐宏祥[8]針對由一個零售商和一個供應商組成的二級供應鏈，建立了分散式供應鏈和VMI模式供應鏈的模型，比較了兩種模式供應鏈的性能，并進一步給出了提高VMI模式供應鏈性能的有效途徑；劉鵬飛[9]考慮需求與零售商努力水平滿足相乘型時，研究了集成VMI和分散VMI決策下的最優努力水平，并提出了采用零售商承擔供應商部分滯銷成本，供應商分擔零售商部分努力成本的VMI模式下的改進批發價格契約來協調供應鏈，同時說明了該契約可使VMI供應鏈達到完美協調，且零售商和供應商獲得集成VMI收益的比例等于供應商和零售商各自在VMI中承擔的努力水平和滯銷成本的比例。

從上述研究可以看出，現今針對VMI模式下供應鏈的批發價格契約與協調的研究均假定供應鏈參與人是完全自利的，即只追求自身利益最大化，而對其它供應鏈參與人的利益漠不關心。而Camerer和Thaler[10]通過研究最后通牒博弈，揭示了人們會放棄一定收益來懲罰對其不公的人。Rabin[11]則最先定義了公平關切，并認為人們往往會傾向于懲罰對其不公的人。此后，Fehr和Schmidt[12]提出了不公平厭惡模型來刻畫公平關切，并認為無論自身利益高于或低于他人利益均會感到不公平厭惡，同時會產生效用損失；Bolton和Ockenfels[13]則提出了ERC公平偏好模型，同樣指出了收益差異會產生不公平厭惡，但認為人們產生不公平厭惡源于自身利益與群體平均利益的差異，而不是與其他個人利益的差異。Cui等[14]最先將不公平厭惡的概念引入到傳統的二級供應鏈中，并對供應鏈的協調問題進行了研究，說明了當零售商的不公平厭惡系數滿足一定條件時合適的批發價格契約可使供應鏈達到協調。此后，一些國內外學者針對傳統供應鏈庫存管理模式下考慮不公平厭惡(或公平關切)的供應鏈協調問題開展了相關的研究工作[15-20]。需要指出的是，目前針對VMI模式下考慮不公平厭惡的供應鏈的批發價格契約與協調的研究成果尚不多見。鑒于此，本文則是依據傳統供應鏈庫存管理模式下考慮不公平厭惡(或公平關切)的供應鏈協調問題研究的基本思路[15-20]，針對由單一供應商與單一零售商組成的二級VMI供應鏈協調問題，在供應商存在不公平厭惡的假設下，運用文獻[14]提出的不公平厭惡模型來刻畫供應商的不利與有利不公平厭惡，通過分析得到分散VMI供應鏈情形下供應商的最優策略，并進一步分析此二級VMI供應鏈在批發價格契約下的協調情況，最后通過數值實驗分析驗證相關研究結論。

2 問題描述與基本模型

考慮一個經營單一時令性產品的VMI模式下的二級供應鏈，其由一個供應商與一個零售商構成。假定此二級供應鏈的信息是完全共享的，且供應商與零售商簽訂批發價格契約合同。

在銷售季前，供應商依據批發價格契約生產相應的產品，且單位生產成本為c，產品生產量為q。在銷售季中，零售商銷售產品給顧客，且單位銷售價格為p，單位批發價格為w；該產品的市場需求量D∈[0,+∞)為一個隨機變量，并假定隨機需求量D的分布函數與概率密度函數分別為F(x)和f(x)，其期望為E(D)=μ，且F(x)是連續、可微及嚴格遞增的，F(0)=0；若在銷售季中出現缺貨的情形，則零售商所承擔的單位缺貨成本為gr，供應商所承擔的單位缺貨成本為gs；若在銷售季中出現產品生產過量的情形，由于VMI模式下供應商自主管理產品庫存，則供應商需承擔相應的庫存費用，且供應商所承擔的單位庫存成本為h。在銷售季末，若仍有剩余的產品未被銷售，則供應商將對剩余產品進行季末處理，且單位剩余產品的凈殘值為v。依據客觀現實的合理性，則有p>w>c>v>0，gr,gs,h>0。

分散VMI供應鏈情形下，零售商的利潤πr(q)可被表示為:

πr(q)=pmin{D,q}-wmin{D,q}-grmax{D-q,0}

(1)

進一步地，依據式(1)，可計算得到零售商的期望利潤E(πr(q))，即:

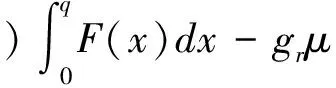
(2)

分散VMI供應鏈情形下，供應商的利潤πs(q)可被表示為:

πs(q)=wmin{D,q}+vmax{q-D,0}-hmax{q-D,0}-cq-gsmax{D-q,0}

(3)

進一步地，依據式(3)，可計算得到供應商的期望利潤E(πs(q))，即:

(4)

依據式(1)和(3)，集中VMI供應鏈情形下供應鏈的總利潤π(q)可被表示為:

π(q)=pmin{D,q}+vmax{q-D,0}-hmax{q-D,0}-(gr+gs)max{D-q,0}-cq

(5)

進一步地，可計算得到集中供應鏈情形下供應鏈的總期望利潤E(π(q))，即:

(6)

針對式(6)求關于q的一階與二階導數，即：

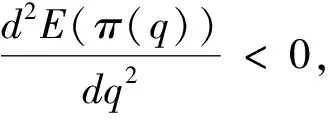
3 不公平厭惡下批發價格契約與協調

若供應商存在不公平厭惡，其進行決策時不僅要考慮自身利潤πs(q)，同時還要考慮分配是否公平。依據Cui等[14]提出的不公平厭惡模型，不公平厭惡供應商的效用函數可被表示為：

U(πs)=πs(q)+us(q)

(7)

其中，us(q)為分配不公平所產生的負效用，us(q)可進一步地展開為：

us(q)=-αmax{λπr(q)-πs(q),0}-βmax{πs(q)-λπr(q),0}

(8)

其中，α∈[0,+∞)為不利不公平厭惡系數，即供應商對不利不公平的厭惡程度，且當α=0時，則表明供應商為傳統供應商(即風險中性的供應商)，當α∈(0,+∞)，則表明供應商存在不利不公平厭惡，且供應商的不利不公平厭惡隨著不利不公平厭惡系數α的增加而增強；β∈[0,1)為有利不公平厭惡系數，即供應商對有利不公平的厭惡程度，且當β=0時，則表明供應商為傳統供應商，當β∈(0,1)時，則表明供應商存在有利不公平厭惡，且供應商的有利不公平厭惡隨著有利不公平厭惡系數β的增加而增強；λ∈(0,+∞)為零售商勢力外生參數，反應零售商在供應鏈中的勢力優勢程度，若λ∈(0,1)，則表明零售商處于弱勢地位，且λ越小，零售商的弱勢地位表現的越明顯，若λ=1，則表明零售商與供應商處于同等的地位，若λ∈(1,+∞)，則表明零售商處于優勢地位，且λ越大，零售商的優勢地位表現的越明顯。Loewenstein等[21]通過實驗驗證了不利不公平厭惡系數α和有利不公平厭惡系數β的大小關系，即α≥β，其認為參與者的不利不公平厭惡程度比有利不公平厭惡程度大。

由式(7)可知，不公平厭惡供應商的效用由兩部分構成，即供應商的自身利潤πs(q)與分配不公平所產生的負效用us(q)。進一步地，由式(8)可知，供應商的公平是相對于零售商而言的，即供應商所認為的公平收益為零售商收益的一部分λπr(q)，當供應商的利潤低于其所認為的公平收益時，供應商就會感到不利不公平厭惡，而當供應商的利潤高于其所認為的公平收益時，供應商就會感到有利不公平厭惡。

下面將針對由單一供應商與單一零售商組成的二級VMI供應鏈協調問題，在供應商存在不利與有利不公平厭惡的情形下，通過分析得到分散VMI供應鏈情形下供應商的最優策略，并進一步分析此二級VMI供應鏈在批發價格契約下的協調情況。

3.1 不利不公平厭惡下批發價格契約與協調

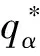
在供應商存在不利不公平厭惡的情形下，即λπr(q)-πs(q)≥0，依據式(1)、(3)、(7)和(8)，則不利不公平厭惡供應商的效用函數U(πs)可被表示為：

U(πs)=πs(q)-α(λπr(q)-πs(q))=(1+α)πs(q)-αλπr(q)，α∈[0,+∞),λ∈(0,+∞)

(9)

進一步地，計算得到不利不公平厭惡供應商的期望效用函數E(U(πs))，即：

(10)

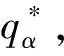
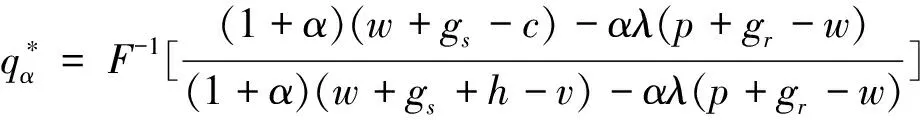
證明 針對式(10)求關于q的一階與二階導數，即：

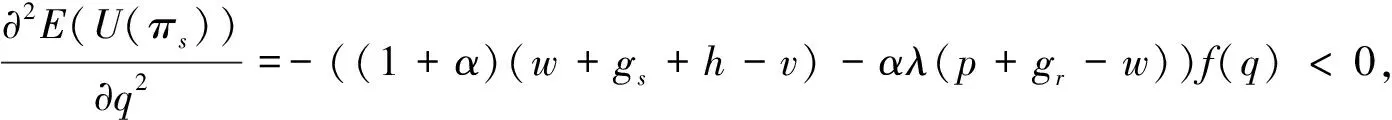
進一步整理得到：

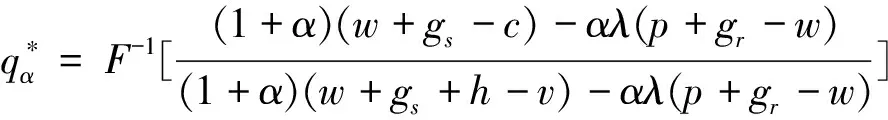
證畢。

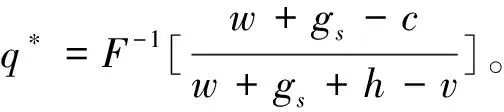
定理2 對于?λ∈(0,+∞)，不利不公平厭惡供應商的最優產品生產量不高于傳統供應商的最優產品生產量，且其為不利不公平厭惡系數的嚴格減函數。

進一步地，可知

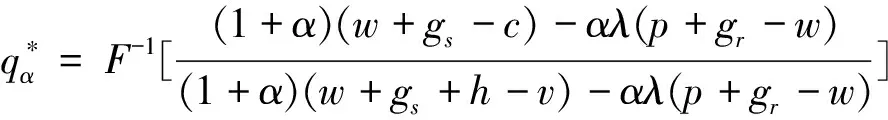
定理2揭示了在零售商勢力外生參數一定的情形下，不利不公平厭惡供應商的最優產品生產量與傳統供應商的最優產品生產量的關系，即不利不公平厭惡供應商的最優產品生產量始終不高于傳統供應商的最優產品生產量，這就說明了當供應商的利潤低于其所認為的公平收益時，不利不公平厭惡供應商會減少其最優產品生產量；同時，定理2亦說明了在零售商勢力外生參數一定的情形下，不利不公平厭惡供應商的最優產品生產量與不利不公平厭惡系數的關系，即不利不公平厭惡供應商的最優產品生產量為不利不公平厭惡系數的嚴格減函數，這就說明了隨著供應商的不利不公平厭惡程度的增加，不利不公平厭惡供應商的最優產品生產量是減少的。

定理3 對于?α∈[0,+∞)，不利不公平厭惡供應商的最優產品生產量不高于傳統供應商的最優產品生產量，且其為零售商勢力外生參數的減函數。

進一步地，可知

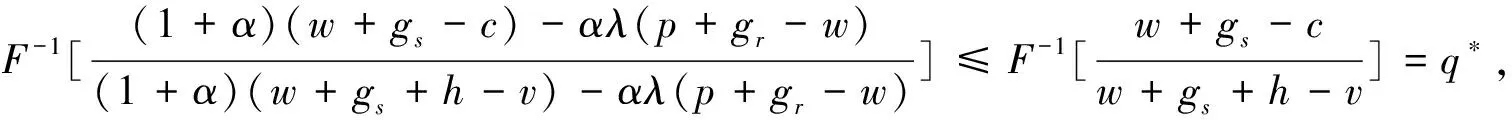
定理3揭示了在不利不公平厭惡系數一定的情形下，不利不公平厭惡供應商的最優產品生產量與傳統供應商的最優產品生產量的關系，即不利不公平厭惡供應商的最優產品生產量始終不高于傳統供應商的最優產品生產量，這就說明了當供應商的利潤低于其所認為的公平收益時，不利不公平厭惡供應商會減少其最優產品生產量；同時，定理3亦說明了在不利不公平厭惡系數一定的情形下，不利不公平厭惡供應商的最優產品生產量與零售商勢力外生參數的關系，即不利不公平厭惡供應商的最優產品生產量為零售商勢力外生參數的減函數，這就說明了隨著零售商在二級VMI供應鏈中勢力優勢程度的增加，不利不公平厭惡供應商的最優產品生產量是減少的。

定理4 在供應商存在不利不公平厭惡的情形下，批發價格契約不能協調二級VMI供應鏈。

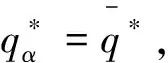
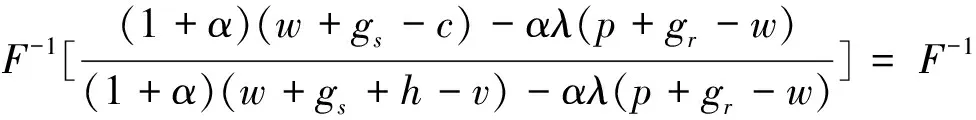
若α+αλ≠-1，則有w=p+gr或v=c+h。由于p>w，gr>0，c>v，h>0，則w≠p+gr或v≠c+h恒成立，故在供應商存在不利不公平厭惡的情形下，批發價格契約不能協調二級VMI供應鏈。

若α+αλ=-1，則有：

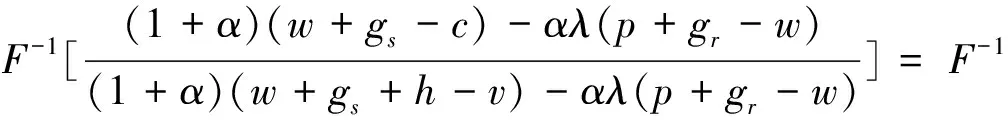
定理4表明：在供應商存在不利不公平厭惡的情形下，二級VMI供應鏈在批發價格契約下是無法達到協調的，即當供應商的利潤低于其所認為的公平收益時，不利不公平厭惡供應商的最優產品生產量始終達不到集中VMI供應鏈情形下供應鏈的最優產品生產量，從而不能使二級VMI供應鏈達到協調。定理4的管理啟示是：供應商的不利不公平厭惡對二級VMI供應鏈是不利的，即供應商的不利不公平厭惡使得二級VMI供應鏈在批發價格契約下無法達到協調，故在現實的二級VMI供應鏈管理中，應盡可能避免引起供應商的不利不公平厭惡。

3.2 有利不公平厭惡下批發價格契約與協調

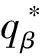
在供應商存在有利不公平厭惡的情形下，即πs(q)-λπr(q)≥0，依據式(1)、(3)、(7)和(8)，則有利不公平厭惡供應商的效用函數U(πs)可被表示為：

U(πs)=πs(q)-β(πs(q)-λπr(q))=(1-β)πs(q)+βλπr(q),β∈[0,1),λ∈(0,+∞)

(11)

進一步地，計算得到有利不公平厭惡供應商的期望效用函數E(U(πs))，即：

(12)

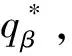
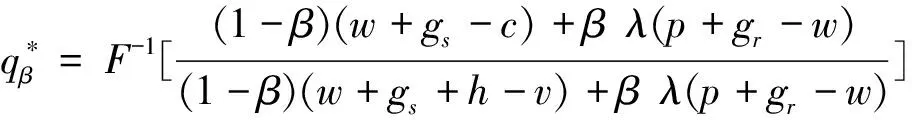
證明 針對式(12)求關于q的一階與二階導數，即：

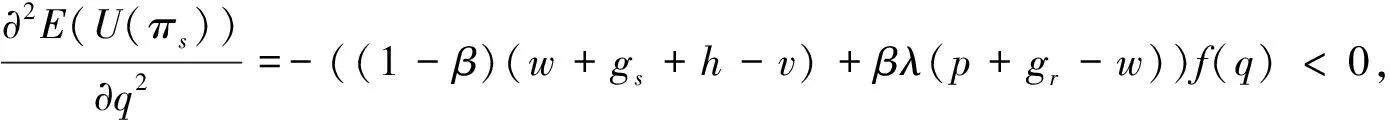
進一步整理得到：

證畢。

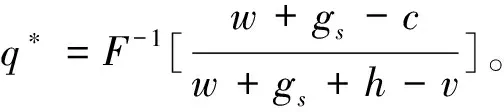
定理6 對于?λ∈(0,+∞)，有利不公平厭惡供應商的最優產品生產量不低于傳統供應商的最優產品生產量，且其為有利不公平厭惡系數的嚴格增函數。

進一步地，可知

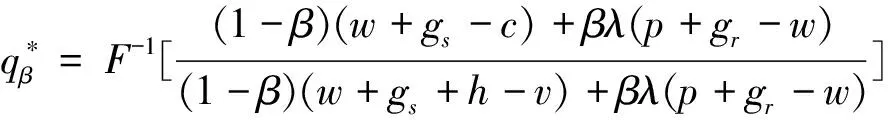
定理6揭示了在零售商勢力外生參數一定的情形下，有利不公平厭惡供應商的最優產品生產量與傳統供應商的最優產品生產量的關系，即有利不公平厭惡供應商的最優產品生產量始終不低于傳統供應商的最優產品生產量，這就說明了當供應商的利潤高于其所認為的公平收益時，有利不公平厭惡供應商會增加其最優產品生產量；同時，定理6亦說明了在零售商勢力外生參數一定的情形下，有利不公平厭惡供應商的最優產品生產量與有利不公平厭惡系數的關系，即有利不公平厭惡供應商的最優產品生產量為有利不公平厭惡系數的嚴格增函數，這就說明了隨著供應商的有利不公平厭惡程度的增加，有利不公平厭惡供應商的最優產品生產量亦是增加的。

定理7 對于?β∈[0,1)，有利不公平厭惡供應商的最優產品生產量不低于傳統供應商的最優產品生產量，且其為零售商勢力外生參數的增函數。

進一步地，可知

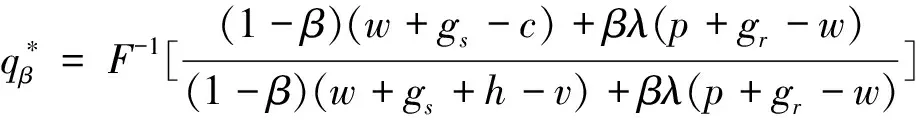
定理7揭示了在有利不公平厭惡系數一定的情形下，有利不公平厭惡供應商的最優產品生產量與傳統供應商的最優產品生產量的關系，即有利不公平厭惡供應商的最優產品生產量始終不低于傳統供應商的最優產品生產量，這就說明了當供應商的利潤高于其所認為的公平收益時，有利不公平厭惡供應商會增加其最優產品生產量；同時，定理7亦說明了在有利不公平厭惡系數一定的情形下，有利不公平厭惡供應商的最優產品生產量與零售商勢力外生參數的關系，即有利不公平厭惡供應商的最優產品生產量為零售商勢力外生參數的增函數，這就說明了隨著零售商在二級VMI供應鏈中的勢力優勢程度的增加，有利不公平厭惡供應商的最優產品生產量亦是增加的。

定理8 在供應商存在有利不公平厭惡的情形下，若β+βλ=1，則批發價格契約可使二級VMI供應鏈達到協調。

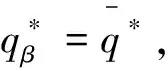
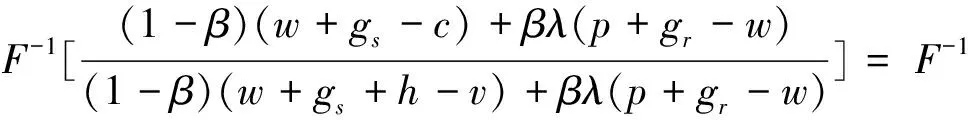
若β+βλ=1，則有

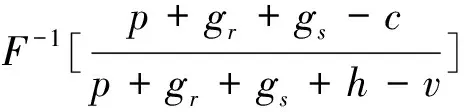
定理8表明：在供應商存在有利不公平厭惡的情形下，批發價格契約在一定條件下可使二級VMI供應鏈達到協調，即當供應商的利潤高于其所認為的公平收益時，有利不公平厭惡供應商的最優產品生產量在一定條件(β+βλ=1)下可達到集中VMI供應鏈情形下供應鏈的最優產品生產量，進而使二級VMI供應鏈達到協調。定理8的管理啟示是：若現實中零售商在二級VMI供應鏈中的優勢地位越明顯(即零售商勢力外生參數λ越大)，則供應商的有利不公平厭惡程度越低(即有利不公平厭惡系數β越小)，越有利于二級VMI供應鏈在批發價格契約下的協調；若現實中零售商在二級VMI供應鏈中的弱勢地位越明顯(即零售商勢力外生參數λ越小)，則供應商的有利不公平厭惡程度越高(即有利不公平厭惡系數β越大)，越有利于二級VMI供應鏈在批發價格契約下的協調。

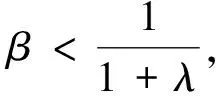
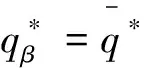
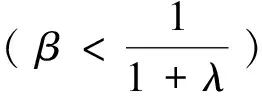
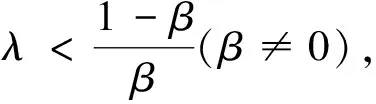
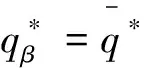
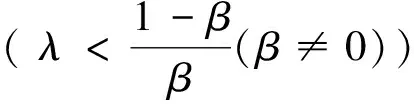
4 數值實驗

本節針對由單一供應商與單一零售商組成的二級VMI供應鏈，在供應商存在不利與有利不公平厭惡的情形下，通過數值實驗分析批發價格契約下不利不公平厭惡系數、有利不公平厭惡系數及零售商勢力外生參數對最優產品生產量及利潤(零售商的期望利潤、供應商的期望利潤和供應鏈的總期望利潤)的影響，從而驗證本文得出的相關結論。

4.1 不利不公平厭惡系數及零售商勢力外生參數對最優產品生產量及利潤的影響

設市場需求服從正態分布D～N(400,1002)，并依據客觀現實的合理性，即p>w>c>v>0，gr,gs,h>0，將二級VMI供應鏈的參數設置如下：p=60，w=45，c=30，v=15，gr=5，gs=h=10，α=0.5，λ=1。

1)在上述參數設置前提下，將不利不公平厭惡系數α視為變量，當不利不公平厭惡系數α=0時，分散VMI供應鏈情形下傳統供應商的最優產品生產量為400，且小于集中VMI供應鏈情形下的最優產品生產量437。同時，當不利不公平厭惡系數α∈[0,+∞)從0增加到10時，最優產品生產量與供應鏈的總期望利潤均是減少的(如表1所示)，且分散VMI供應鏈情形下的最優產品生產量始終不高于傳統供應商的最優產品生產量。因此，在供應商存在不利不公平厭惡的情形下批發價格契約無法協調二級VMI供應鏈。

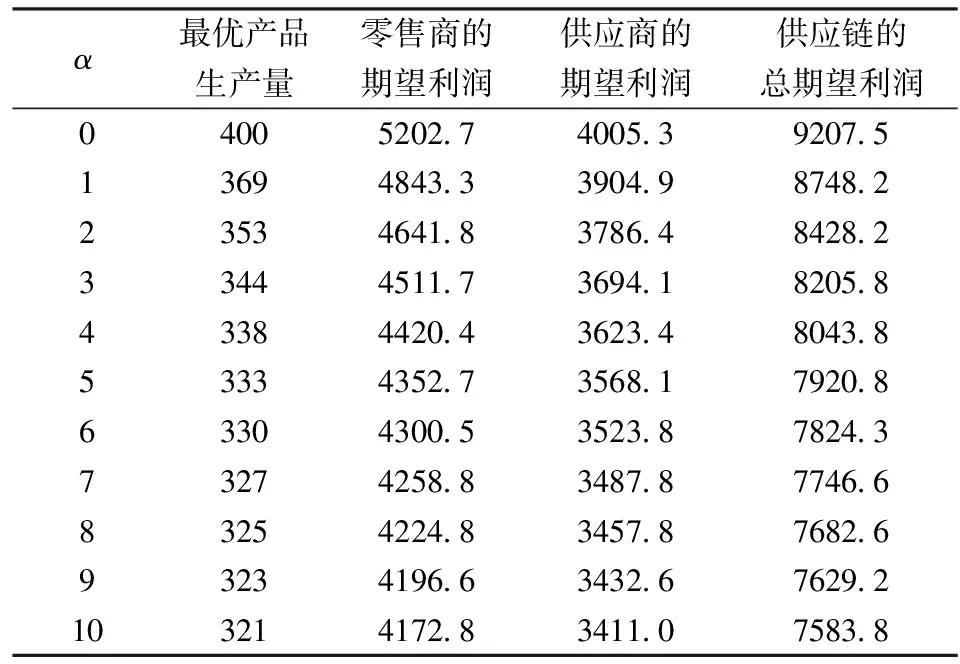
表1 α對最優產品生產量及利潤的影響

2)當不利不公平厭惡系數α=0時，分散VMI供應鏈情形下傳統供應商的最優產品生產量為400，且小于集中VMI供應鏈情形下的最優產品生產量437。在上述參數設置前提下，將零售商勢力外生參數λ視為變量，當零售商勢力外生參數λ∈(0,+∞)從0.3增加到3時，最優產品生產量與供應鏈的總期望利潤均是減少的(如表2所示)，且分散VMI供應鏈情形下的最優產品生產量始終不高于傳統供應商的最優產品生產量。因此，在供應商存在不利不公平厭惡的情形下批發價格契約無法協調二級VMI供應鏈。

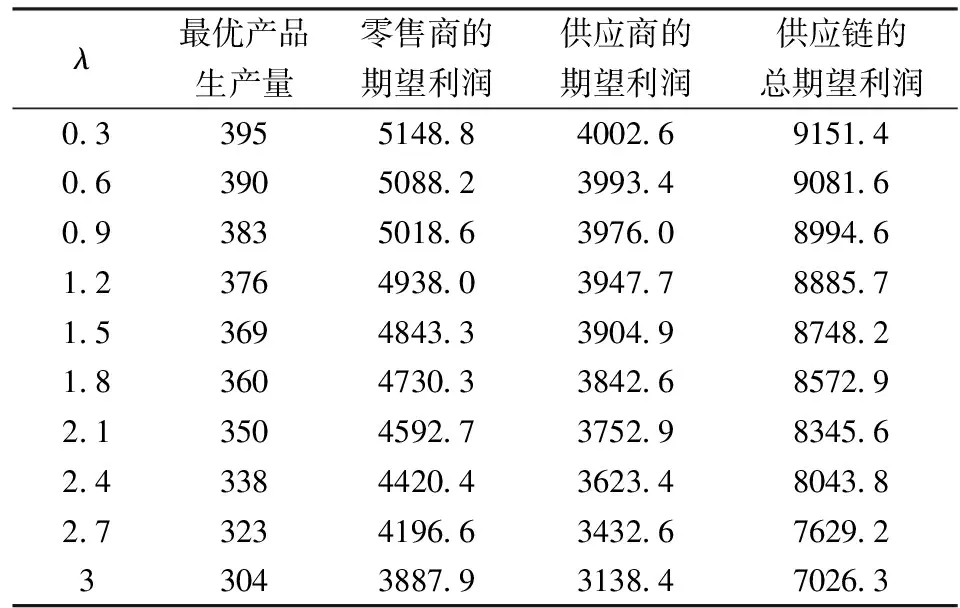
表2 λ對最優產品生產量及利潤的影響

4.2 有利不公平厭惡系數及零售商勢力外生參數對最優產品生產量及利潤的影響

設市場需求服從正態分布D～N(400,1002)，并依據客觀現實的合理性，即p>w>c>v>0，gr,gs,h>0，將二級供應鏈的參數設置如下：p=50，w=45，c=30，v=15，gr=5，gs=h=10，β=0.2，λ=1。

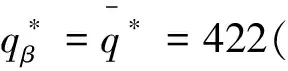
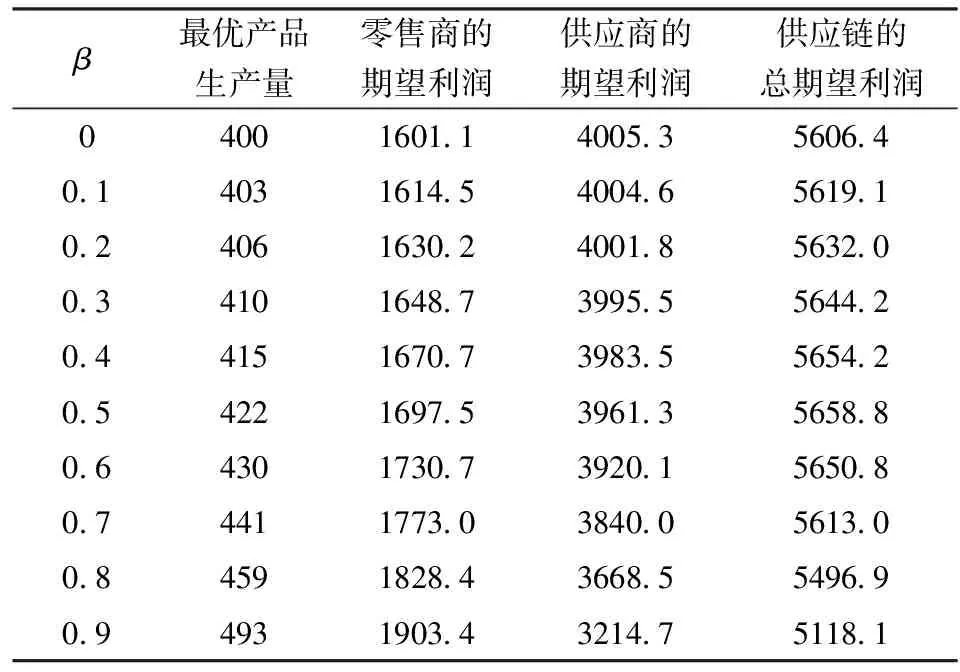
表3 β對最優產品生產量及利潤的影響

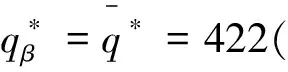
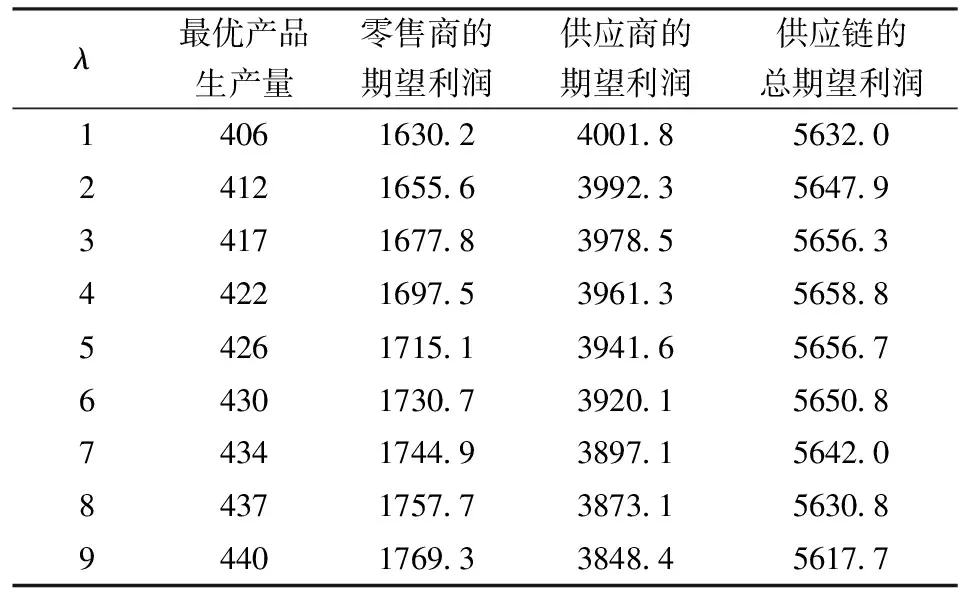
表4 λ對最優產品生產量及利潤的影響

5 結語

本文針對由單一供應商與單一零售商組成的二級VMI供應鏈協調問題，在供應商存在不利與有利不公平厭惡的情形下，運用文獻[14]提出的不公平厭惡模型來刻畫供應商的兩種不公平厭惡，通過分析得到了分散VMI供應鏈情形下供應商的最優策略及其相關性質，并針對此二級VMI供應鏈在批發價格契約下的協調情況進行了分析，最后通過數值實驗分析驗證了相關研究結論。與已有相關研究不同的是，本文著重考慮了VMI模式下二級供應鏈中供應商存在不公平厭惡的情形，并分析了此二級VMI供應鏈在批發價格契約下的協調情況。通過本文的研究，得到以下主要結論：1) 在供應商存在不利不公平厭惡的情形下，供應商存在唯一的最優產品生產量，其不高于傳統供應商的最優產品生產量且為不利不公平厭惡系數或零售商勢力外生參數的嚴格減函數或減函數，批發價格契約無法使二級VMI供應鏈達到協調；2) 在供應商存在有利不公平厭惡的情形下，供應商存在唯一的最優產品生產量，其不低于傳統供應商的最優產品生產量且為有利不公平厭惡系數或零售商勢力外生參數的嚴格增函數或增函數，批發價格契約在一定條件下可使二級VMI供應鏈達到協調。

進一步地，通過本文的研究，得到對供應鏈管理的一些管理啟示如下：1) 在現實的二級VMI供應鏈管理中，應盡可能避免引起供應商的不利不公平厭惡；2) 若現實中零售商在二級VMI供應鏈中的優勢地位越明顯，則供應商的有利不公平厭惡程度越低，越有利于二級VMI供應鏈在批發價格契約下的協調；若現實中零售商在二級VMI供應鏈中的弱勢地位越明顯，則供應商的有利不公平厭惡程度越高，越有利于二級VMI供應鏈在批發價格契約下的協調；3) 若現實中零售商在二級VMI供應鏈中的優勢地位越明顯，則供應商的有利不公平厭惡程度越低，越有利于供應鏈的總期望利潤的最大化；若現實中零售商在二級VMI供應鏈中的弱勢地位越明顯，則供應商的有利不公平厭惡程度越高，越有利于供應鏈的總期望利潤的最大化；4) 若現實中供應商的有利不公平厭惡程度越高，則零售商在二級VMI供應鏈中的弱勢地位越明顯，越有利于供應鏈的總期望利潤的最大化；若現實中供應商的有利不公平厭惡程度越低，則零售商在二級VMI供應鏈中的優勢地位越明顯，越有利于供應鏈的總期望利潤的最大化。

本文進一步的拓展研究方向為：考慮不公平厭惡下VMI供應鏈的收益共享契約與協調等。

[1] 蔡建湖, 黃衛來, 周根貴. 基于收益分享契約的VMI模型研究[J]. 中國管理科學, 2006, 14(4): 108-113.

[2] Waller M, Johnson M E, Davis T. Vendor-managed inventory in the retail supply chain[J]. Journal of Business Logistics, 1999, 20(1): 183-204.

[3] Cetinkaya S, Lee C Y. Stock replenishment and shipment scheduling for vendor-managed inventory systems[J]. Management Science, 2000, 46(2): 217-232.

[4] Yu Yugang, Chu Feng, Chen Haoxun. A stackelberg game and its improvement in a VMI system with a manufacturing vendor[J]. European Journal of Operational Research, 2009, 192(3): 929-948.

[5] Darwish M A, Odah O M. Vendor managed inventory model for single-vendor multi-retailer supply chains[J]. European Journal of Operational Research, 2010, 204(3): 473-484.

[6] 李績才, 周永務, 肖旦, 等. 考慮損失厭惡一對多型供應鏈的收益共享契約[J]. 管理科學學報, 2013, 16(2): 71-82.

[7] Gerchak Y, Wang Y. Revenue-sharing vs. wholesale-price contracts in assembly systems with random demand[J]. Production and Operations Management, 2004, 13(1): 23-33.

[8] 唐宏祥. VMI對供應鏈性能的影響分析[J]. 中國管理科學, 2004, 12(2): 60-65.

[9] 劉鵬飛. 需求依賴零售商努力水平的VMI協調[J]. 系統工程學報, 2012, 27(5): 679-684.

[10] Camerer C, Thaler R H. Anomalies: Ultimatums, dictators and manners[J]. The Journal of Economic Perspectives, 1995, 9(2): 209-219.

[11] Rabin M. Incorporating fairness into game theory and economics[J]. Advances in Behavioral Economics, 1993, 83(5): 1281-1302.

[12] Fehr E, Schmidt K M. A theory of fairness, competition, and cooperation[J]. The Quarterly Journal of Economics, 1999, 114(3): 817-868.

[13] Bolton G E, Ockenfels A. ERC: A theory of equity, reciprocity, and competition[J]. American Economic Review, 2000, 90(1): 166-193.

[14] Cui T H, Raju J S, Zhang Z J. Fairness and channel coordination[J]. Management Science, 2007, 53(8): 1303-1314.

[15] Caliskan-Demirag O, Chen Youhua, Li Jianbin. Channel coordination under fairness concerns and nonlinear demand[J]. European Journal of Operational Research, 2010, 207(3): 1321-1326.

[16] 杜少甫, 杜嬋, 梁樑, 等. 考慮公平關切的供應鏈契約與協調[J]. 管理科學學報, 2010, 13(11): 41-48.

[17] 丁川, 王開弘, 冉戎. 基于公平偏好的營銷渠道合作機制研究[J]. 管理科學學報, 2013, 16(8): 80-94.

[18] 畢功兵, 翟安民, 梁樑. 不公平厭惡下供應鏈的批發價格契約與協調[J]. 系統工程理論與實踐, 2013, 33(1): 134-140.

[19] 李建斌, 劉鳳, 雷東. 基于公平參數的供應鏈柔性合同優化策略[J]. 系統工程理論與實踐, 2013, 33(7): 1791-1800.

[20] 馬利軍, 曾清華, 邵新建. 冪函數需求模式下具有公平偏好的供應鏈協調[J]. 系統工程理論實踐, 33(12): 3009-3019.

[21] Loewenstein G F, Thompson L, Bazerman M H. Social utility and decision making in interpersonal contexts[J]. Journal of Personality and Social Psychology, 1989, 57(3): 426-441.

[22] Cachon G P. Supply chain coordination with contract[J]. Handbooks in Operation and Managements Science,2003,11: 229-339.

VMI Supply Chain Coordination with Wholesale Price Contract Incorporating Unfair Aversion

LIU Yun-zhi, FAN Zhi-ping

(School of Business Administration, Northeastern University, Shenyang 110169, China)

Supply chain contract is an important factor in affecting the overall performance of VMI supply chain, so the supply chain contract has become a noteworthy research topic recently. In this paper the two-stage VMI supply chain coordination problem is investigated with a single supplier and a single retailer. Based on unfair aversion supplier assumption, the supplier’s disadvantageous unfair aversion and advantageous unfair aversion are portrayed by the unfair aversion model. Then, the supplier’s optimal strategies are analyzed at the distributed VMI supply chain. And the two-stage VMI supply chain coordination problem with wholesale price contract is studied. By the analysis, the main conclusions can be obtained as follows: for a disadvantageous unfair-averse supplier, there is a unique optimal production quantity which is less than the traditional supplier’s optimal production quantity and strictly decreases (decreases) with the disadvantageous unfair-averse coefficient (retailer’s exogenous-force parameter), the wholesale price contract cannot coordinate the two-stage VMI supply chain; for a advantageous unfair-averse supplier; there is a unique optimal production quantity which is more than the traditional supplier’s optimal production quantity and strictly increases (increases) with the advantageous unfair-averse coefficient (retailer’s exogenous-force parameter), the wholesale price contract can coordinate the two-stage VMI supply chain under certain conditions. Finally, numerical examples are used to prove the findings.

VMI；supply chain coordination；unfair aversion；wholesale price contract

1003-207(2016)04-0063-11

10.16381/j.cnki.issn1003-207x.2016.04.008

2014-07-21；

2015-04-13

國家自然科學基金資助項目(71271051)；中央高校基本科研業務經費資助項目(N140607001, N130606001)

劉云志(1985-)，男(漢族)，遼寧遼陽人，東北大學工商管理學院，博士研究生，研究方向：運作管理與決策分析,E-mail:yunzhi_liu@126.com.

F274; C931

A