配額-交易機制下動態批量生產和減排投資策略研究
黃 帝, 陳 劍, 周 泓
(1. 北京交通大學經濟管理學院,北京 100044;2. 清華大學經濟管理學院,北京 100084;3. 北京航空航天大學經濟管理學院,北京 100191)
?
配額-交易機制下動態批量生產和減排投資策略研究
黃 帝1, 2, 陳 劍2, 周 泓3
(1. 北京交通大學經濟管理學院,北京 100044;2. 清華大學經濟管理學院,北京 100084;3. 北京航空航天大學經濟管理學院,北京 100191)
隨著我國碳排放交易市場的建立和發展,在碳排放約束下逐步降低單位產出的碳排放水平成為企業生產經營管理中的中長期約束性目標。本文在一個多周期決策模型中研究了配額-交易機制下企業的最優動態批量生產、碳排放權交易和減排投資聯合決策問題。生產商在整個決策周期期初決定是否進行減排投資以及投資規模,根據每個周期的生產計劃決定減排設備的運行計劃。根據節能減排技術的特點,本文假設生產商運行減排設備時不僅降低了產品的單位生產碳排放量,而且降低了產品的單位生產成本。本文基于廣義Benders分解法對模型進行了最優性分析,得到了最優生產決策和最優減排投資決策的一些基本性質,并通過數值實驗分析了碳排放配額和碳排放權價格對生產商總成本、總排放以及減排投資決策的影響。本文的數值實驗分析結果發現:(1)當碳交易市場上的碳排放權充足時,減少碳排放配額或改變碳排放配額的分配方式并不能影響生產商的碳排放水平;(2)碳排放權價格是影響生產商的碳排放水平和減排投資規模的關鍵因素;(3)隨著碳排放權價格的上升,即使擁有足夠的碳排放配額,生產商仍會不斷提高減排投資規模以獲得減排收益。研究結果對碳排放交易體系下生產企業進行減排技術投資具有較強的管理啟示。
動態批量;減排投資;配額-交易;廣義Benders分解
1 引言
近年來,環境保護和經濟發展之間的矛盾愈加突出。一方面,全球氣候變暖使人們認識到經濟、社會和環境協調發展的重要性,以低能耗、低污染為理念的低碳經濟成為人類社會可持續發展的必然選擇。另一方面,隨著經濟的發展,全球能源需求仍在繼續增加。國際能源署(IEA)預測,全球能源需求量到2035年將至少增長三分之一。工業是國民經濟的重要組成部分,是推動經濟增長的主要動力,也是能源消費及二氧化碳等溫室氣體排放的主要領域。為實現經濟持續健康發展,降低工業生產中的二氧化碳排放量成為國民經濟發展中的長期約束性指標,也成為當前學術研究的熱點。
碳排放規則是指國際社會為應對全球氣候變暖給人類生存和發展帶來的嚴峻挑戰而采取的一系列控制二氧化碳等溫室氣體排放的政策措施。配額—交易機制作為一種二氧化碳排放總量控制手段,被中國、美國、澳大利亞和歐盟等國家和地區廣泛使用。它通過總量控制和市場調節相結合的手段,引導和鼓勵企業在節能減排技術和可再生能源領域進行投資,實現經濟社會的總體減排。在碳排放權交易市場中,碳排放權被賦予特定的產權,可以在市場上進行轉讓、交換等交易活動,通過碳排放權價格的調節來實現環境資源的合理配置。1997年12月制定的國際公約《京都議定書》提出了旨在減排的三個靈活合作機制:聯合履約、清潔發展和碳排放權交易機制。此后,美國、澳大利亞、歐盟和中國等國家和地區都相繼建立起了碳排放權交易市場。以配額—交易機制為核心的歐洲碳排放權交易體系(EU-ETS)自2005年至今已運行三個階段,在減少二氧化碳等溫室氣體排放方面取得了初步成效。我國自2012年以來在北京、天津、上海、重慶、深圳、廣東和湖北等七個省市逐步開展碳排放交易試點工作。截止2014年6月19日,七個碳排放權交易試點省市已全部開始實際交易。目前,廣東碳交易市場已發展成為僅次于歐盟、韓國的全球第三大碳交易市場。
碳排放規則的實施給企業帶來了諸多管理挑戰,逐步降低碳排放水平成為企業生產經營管理中的中長期約束性指標。本文在一個多周期決策模型中研究配額—交易機制下企業的最優生產計劃和減排計劃,分析減排投資成本、碳排放價格、產品需求等參數對企業生產和減排決策的影響,著力解決以下幾個企業運營管理中的關鍵問題:(1) 企業何時投資減排設備?(2) 企業何時運行減排設備?(3) 企業如何安排生產計劃?這些都是在企業管理實踐中迫切需要解決,但目前又尚未進行深入研究的管理問題。對于這些問題的研究無論是從理論層面還是從企業運作層面都具有非常重要的意義
目前對于低碳背景下企業生產和減排投資問題的研究主要集中在兩個方向。第一個研究方向是碳排放約束下的批量生產問題研究。Hua Guowei等[1]研究了配額—交易機制下碳排放權交易價格和碳排放權配額對企業的經濟訂貨批量、總排放和總成本的影響。Benjaafar等[2]在動態批量生產模型中研究了碳稅、配額—交易、配額—抵消等不同的碳政策下單個企業及供應鏈的多周期生產庫存決策問題。他們還通過數值實驗分析了碳排放權配額、碳政策、節能減排技術和供應鏈聯合減排等因素對企業總排放和總成本的影響。Absi等[3]研究了動態批量模型在周期性單位生產碳排放約束、累積周期單位生產碳排放約束、滾動周期單位生產碳排放約束和全周期單位生產碳排放約束等約束條件下的算法時間復雜度。他們證明只有周期性單位生產碳排放約束下的動態批量模型存在多項式時間算法。胡海菊和李勇建[4]利用系統動力學仿真工具對考慮再制造和產品需求可替代的動態批量生產問題進行了建模分析。戴道明[5]研究了產品動態定價與批量生產的聯合決策問題,分析了不同碳政策情形下碳排放配額、碳排放交易價格和碳稅對企業利潤和碳排放水平的影響。
第二個研究方向是企業碳減排投資決策問題研究。王明喜等[6]指出,企業在生產環節可以通過減排設備投資、減排研發投資和能源投入結構調整三個方面來降低其單位產值的二氧化碳排放量。趙道致和張學強[7]研究了考慮總成本和總排放量兩個優化目標的供應鏈網絡設計和優化問題。他們假設生產商有多種可供選擇的技術手段,分別對應不同的單位產品碳減排量和減排投資額。謝鑫鵬和趙道致[8-9]研究了單周期兩級供應鏈的定價和減排決策,但他們在研究中假設減排投資對產品的單位生產成本沒有影響。杜少甫等[10]認為企業的碳減排來自于對排放物的凈化處理,他們分別研究了確定的凈化水平和可變的凈化水平下企業的生產決策和碳排放權交易決策。此后,杜少甫等[10]的工作被何大義和馬洪云[11]和侯玉梅等[12]分別擴展到不確定性需求情形下和雙寡頭企業情形下。陳伯成和李英杰[13]對杜少甫等[10]的工作進行了補充研究,豐富了對企業最優決策結果的分析和參數敏感性分析。Islegen等[14]對碳捕捉與存儲技術的投資決策進行了經濟性分析。Jiang Yan等[15]對比分析了不同碳政策下企業的總利潤、總排放量、減排投資額及投資時機等決策。駱瑞玲等[16]在一個兩級供應鏈中研究了配額—交易機制下供應鏈減排技術投資決策問題,分析了不同決策情形下消費者碳足跡敏感系數、碳排放配額和碳減排成本系數對供應鏈碳排放總量、供應鏈利潤、碳減排投資水平等的影響。王明喜等[17]給出了碳排放約束下我國企業在生產技術、清潔能源和節能管理三條減排路徑上的最優減排投資決策,分析了“強制減排”和“自愿減排”兩種措施下不同的碳排放配額分配方式和企業間碳交易模式對企業實施最優減排投資的影響。陳伯成等[18]假設政府對企業排放凈化量進行補貼、對企業排放量進行懲罰,給出了不同碳政策情形下的最優凈化水平和最優產量。周艷菊等[19]在一個兩級供應鏈中研究了減排成本分擔契約對產品訂貨量和銷售價格的影響,以及消費者低碳認知和低碳情感變化對最優決策的影響。
本文與前述文獻的主要區別在于:1)研究碳排放約束下企業的多周期生產、碳排放交易和減排聯合決策問題。而已有文獻或者只考慮碳排放約束下企業的多周期生產決策問題[2-3,5],或者只考慮單周期的生產和減排聯合決策問題[10-13,16,18-19],少有兩者兼顧。2)結合國內實踐,主要研究企業的減排投資通過降低單位產出的耗能量來實現降低單位產出的碳排放量,即技術減排路徑[17]。而已有文獻認為企業的減排投資僅僅降低單位碳排放量,不影響產品的單位生產成本(包含能耗成本)[8-13,16,18-19]。3)考慮企業在某一周期的減排投資會在后續周期發揮減排效果[17,20]。而大多數文獻在研究中假設企業的減排投資僅在當前決策周期產生減排效果[10-13,16,18-19]。
鑒于此,本文在確定需求環境下研究多周期情形下的動態批量生產、碳排放權交易和減排投資聯合決策問題。生產商在整個決策周期期初決定是否進行減排投資和投資規模,根據每個周期的生產計劃決定減排設備的運行計劃。根據節能減排技術的特點,本文假設生產商運行減排設備時不僅降低了產品的單位生產碳排放量,而且降低了產品的單位生產成本。本文與Benjaafar等[2]的研究不同之處在于,本文在模型中額外考慮了生產商的減排投資決策,而且基于廣義Benders分解得到了生產和減排投資決策的最優性質。分析發現,配額—交易機制下同時考慮碳排放權交易和減排投資時的最優生產決策與經典批量生產問題的最優決策相似,即若生產商在某個周期生產產品,則其生產量必定滿足前后若干個周期的總需求。此外,本文的數值實驗還得到一些與Benjaafar等[2]的數值實驗不同的觀察結果:(1)當碳排放配額固定時,隨著碳價格的升高生產商的碳排放水平不斷下降,而總成本先增加后減少。(2)當碳排放權價格固定時,生產商的減排投資規模不受碳排放配額的影響;當碳排放配額固定時,生產商的減排投資規模隨碳排放權價格的增加不斷上升。(3)當碳排放權價格與碳排放配額呈負相關關系時,隨著碳排放權價格的上升,生產商的碳排放水平不斷下降,而總成本先減少后增加。(4)碳排放配額按周期平均分配與一次性分配的結果相同,即碳排放權的初始分配方式并不影響生產商的決策。
2 問題描述和建模
2.1 問題描述和符號定義
在一個含有T個周期的決策問題中,生產商在第t(t=1,…,T)個周期的市場需求為dt,固定生產成本為St。第t個周期的生產量為Qt,產品的單位生產成本為ct,yt為一個二進制變量,第t個周期生產時為1,不生產時為0。第t個周期期末的庫存水平為It,單位庫存成本為ht。第t個周期期末的延期交貨量為Bt,延期交貨的單位成本為bt。

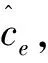
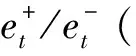
2.2 模型的數學表示
生產商的批量生產、碳排放權交易和減排投資聯合決策模型如下:
(1)
s.t.It-1+Qt+Bt-Bt-1-It=dt,t=1,…,T
(2)
(3)
(4)
yt∈{0,1},t=1,…,T
(5)
0≤xt≤min(Qt,a),t=1,…,T
(6)
(7)
Qt,It,Bt≥0,t=1,…,T
(8)
目標函數(1)中第一項是生產啟動成本;第二項是生產成本;第三項是延期交貨成本;第四項是庫存成本;第五項是碳排放權交易成本(負值表示收益);第六項是減排設備運行成本;第七項是運行減排設備節約的生產成本;最后一項是減排設備投資成本。約束條件(2)是庫存平衡方程;約束條件(3)是整個決策周期內的碳排放平衡約束;約束條件(4)表示產量Qt和yt之間的邏輯關系;約束條件(5) 表示yt是0-1變量;約束條件(6)表示每周期的減排處理量不得超過其投資規模和該周期的生產量;約束條件(7)和(8)是變量的非負性約束。
3 模型的廣義Benders分解
碳排放約束下的動態批量模型及其擴展模型一般都是NP難問題[3],一般的處理方法是將原問題進行分解,以降低求解規模和求解難度。魯奎等[21-22]提出了一種約束松弛的模型分解方法:對耦合約束條件進行拉格朗日松弛,然后將原問題直接拆分為兩個獨立的子問題。但其缺點是被松弛的約束條件對應的拉格朗日乘子被拆分到不同的子問題中,影響了解的質量。有鑒于此,本文使用廣義Benders分解法對原問題進行模型分解,以分析最優解的性質。
由于碳排放權的市場價格在整個決策周期內是固定不變的,不存在投機套利的機會,因此生產商的最優碳排放權交易數量應等于其短缺或剩余的碳排放權數量。故約束條件(3)等價于:
(9)
將約束條件(9)代入到(1)中,可得
(10)
s.t. (2), (4), (5), (6), (8)
廣義Benders分解法[23]的基本思想是,對于給定的復雜變量的每一組值,容易找出剩下的優化問題(子問題)的最優解,在這些最優解中使主問題目標函數值最大的那一組最優解及其對應的復雜變量值即為原問題的最優解。其中,復雜變量是指當其給定時會使原問題的優化變得非常容易的那些變量。根據廣義Benders分解法,將問題(10)分解為一個主問題和一個子問題,其中復雜變量定義為生產商的減排投資決策變量a。
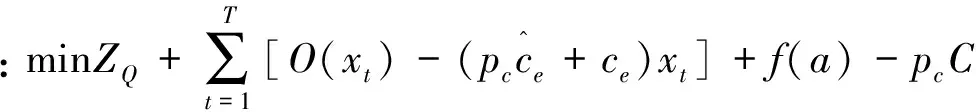
(11)
s.t. (6)
其中,ZQ是下列子問題的最優值:
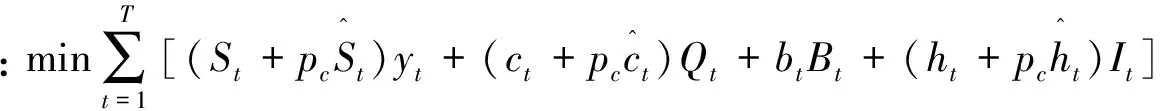
(12)
s.t. (2), (4), (5), (8)
子問題(12)是一個考慮碳排放成本的允許缺貨的動態批量生產模型,它是Wager和Whitin[24]提出的動態經濟批量訂貨模型的擴展形式[25],可以在O(T2)時間內找出問題的最優解[26]。子問題(12)以其最優目標函數值ZQ反饋到主問題(11)的目標函數中,以其最優解Qt反饋到主問題(11)的約束條件(6)中。
值得注意的是,子問題(12)的最優解不受復雜變量a取值的影響。因此,子問題(12)的最優解即為原問題(1)的最優解。子問題(12)的目標函數是線性的,約束條件(2), (4), (5), (8)組成的可行域是封閉的凸集,所以其最優解必在該凸集的頂點處達到。
定理1 子問題(12)的最優解滿足如下性質:
(1)It-1Qt=It-1Bt=ItBt=QtBt=0,t=1,…,T;
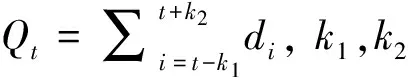
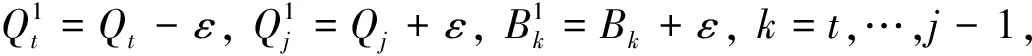
(2)同樣使用反證法:若最優解不滿足(2),易知其必定不滿足(1),則其不是最優解。
證畢。
定理1說明,生產商的最優生產策略應該遵循以下原則:
(1) 庫存水平為0時才進行生產;
(2)有庫存時不允許缺貨;
(3) 若在某個周期進行生產,則該周期不應存在缺貨,即產量至少應該滿足當期需求和該周期之前的所有缺貨;
(4) 一次生產的產量應該等于該周期前后若干個周期的總需求。
定義1 如果Qt>0,則稱周期t為生產周期;如果It>0,則稱周期t為庫存周期;如果Bt>0,則稱周期t為缺貨周期。特別地,如果It=0且Bt=0,則稱周期t為再生周期。
在定理1給出的最優生產策略中,任意兩個連續的再生周期之間存在且僅存在一個生產周期以及若干個庫存周期和缺貨周期。由此,可以給出子問題(12)的動態規劃遞推公式[27]:
(13)
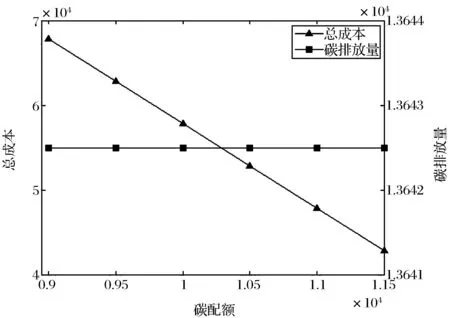
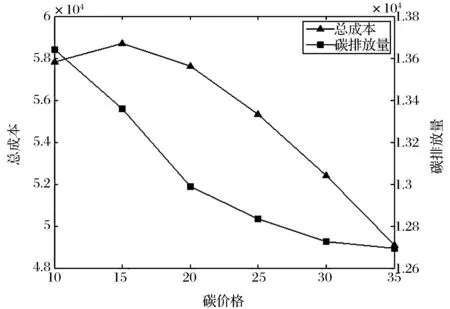
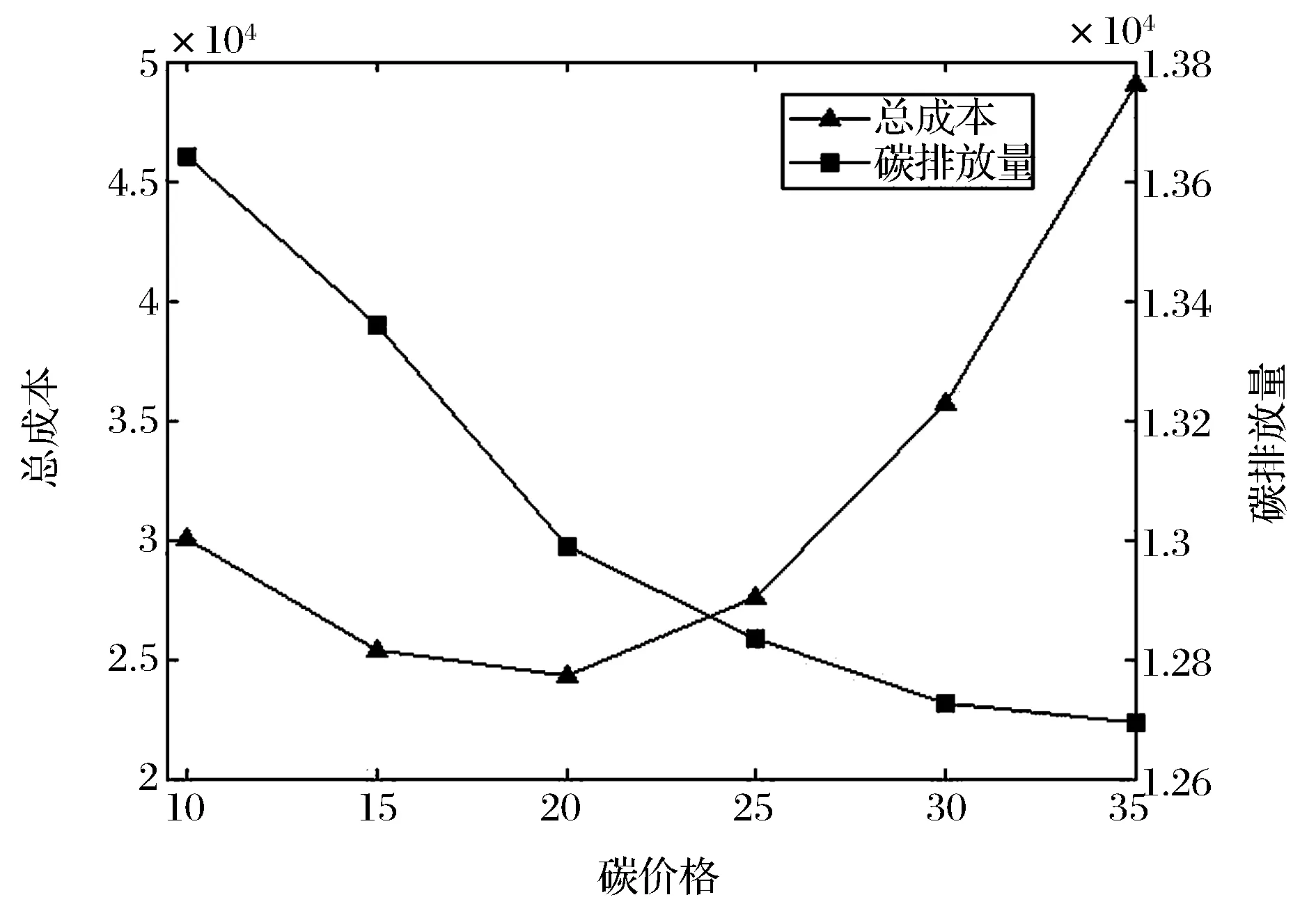
其中,E(j)表示從周期1到周期j的最小總成本,周期i和j表示兩個連續的再生周期(i 一般來說,生產商獲得碳排放權的來源有三種方式:政府分配配額、碳排放權市場交易和生產商投資減排技術[8,10,11,12]。其中,碳排放權配額是由政府管理部門分配的外生變量,其它兩項是由生產商決定的決策變量。當問題(1)的最優生產決策變量由子問題(12)確定后,主問題(11)中生產商的最優減排投資和運行決策滿足如下性質: 生產商在某個決策周期內進行減排設備投資決策時,需要在減排投資和運行總成本與減排總收益之間進行權衡。其中,減排投資和運行總成本包括減排投資成本和每個周期的減排設備運行成本,減排總收益包括每個周期運行減排設備節約的碳排放成本和能耗成本。定理3的管理意義是,當減排投資的邊際收益小于邊際成本時,生產商不進行減排投資。 為了分析配額—交易機制下碳排放權價格pc和碳排放權配額C對企業生產和減排投資決策的影響,在數值實驗中分別對其取不同的值,其中pc={10, 15, 20, 25, 30, 35},C={9000, 9500, 10000, 10500, 11000, 11500}。下列數值實驗結果均通過對隨機生成的25組需求數據進行運算并求其平均值得到。 圖1 碳排放配額對總成本和碳排放量的影響 (1)固定碳排放權的市場價格pc=10,逐漸變化碳排放權配額C發現,生產商的碳排放水平不受碳排放配額的影響,而總成本隨著碳排放權配額的減少不斷上升(圖1)。這是因為從(10)中可以看出, 碳排放權配額C不影響生產商的決策, 與生產商的總成本之間是遞減關系。這個結果說明當碳交易市場上的碳排放權充足時,減少碳排放配額并不能降低生產商的碳排放水平。 圖2 碳價格對總成本和碳排放量的影響 (2)固定碳排放配額C=10000,逐漸變化碳排放權的市場價格pc發現,生產商的碳排放水平隨著碳排放權價格的增加不斷下降,而總成本隨著碳排放價格的增加先增加后減少(圖2)。這是因為隨著碳排放權價格的上升,生產商的碳排放水平不斷下降,減排投資規模不斷上升(表2),生產商由碳排放權不足(支付碳排放權買入成本)逐漸轉變為碳排放權剩余(賣出碳排放權獲得收益)。從圖2中可以看出,當碳排放權價格大于15時,生產商的總成本和碳排放水平隨著碳價格的升高同時降低。 (3) 當碳排放權價格固定時,生產商的減排投資規模不受碳排放配額的影響(表1);當碳排放配額固定時,生產商的減排投資規模隨碳排放權價格的增加不斷上升(表2)。表1-2給出了兩種情況下生產商的實際生產量,減排處理量和最大減排處理能力的統計平均值。從表1可以看出,約96.4%的生產量經過了減排處理,但同時約6.4%的減排能力被閑置。從表2可以看出,雖然在pc=20時生產商的減排投資規模已基本實現對生產量的100%減排處理,但是隨著碳價格的增加,生產商的減排投資規模仍在繼續增加,使得減排能力閑置率由5.9%增加至8.4%。這說明過低的碳排放權價格會抑制減排投資,而過高的碳排放權價格則會引起減排投資過度,減排能力閑置。 表1 不同碳排放配額下的實際生產量,減排處理量和最大減排處理能力(統計平均值) 注:“實際生產量”指整個決策周期內生產商累計生產的數量,它等于總需求量;“減排處理量”指整個決策周期內減排設備累計運行處理的數量;“最大減排處理能力”指減排設備滿負荷運行時處理的數量,它等于減排投資規模乘以生產周期個數。 表2 不同碳排放權價格下的實際生產量,減排處理量和最大減排處理能力(統計平均值) 注:“實際生產量”, “減排處理量”和“最大減排處理能力”的定義同表1。 (4) 當碳排放權價格與碳排放配額呈負相關關系(如pc=125-0.009C)時,生產商的碳排放水平隨著碳排放權價格的增加不斷下降(圖3),生產商的減排投資規模隨著碳排放權價格的增加不斷上升(參見表2)。生產商的總成本隨著碳排放權價格的增加先減少后增加(圖3)。從圖3中可以看出,當碳排放權價格小于20時,生產商的總成本和碳排放水平隨著碳價格的升高同時降低。將pc=125-0.009C代入(10)中可以看出,這是因為生產商的總成本函數(14)中最后一項是關于pc的凸二次函數: (14) s.t. (2), (4), (5), (6), (8) 圖3 碳價格與碳配額負相關時碳價格對總成本和碳排放量的影響 (5)當碳排放配額按周期平均分配給生產商時,與一次性分配碳排放配額的結果相同,生產商的碳排放水平和減排投資規模不受碳排放配額的影響(參見圖1),而總成本隨著碳排放權配額的減少而不斷上升(參見表1)。 假設生產商每個周期得到CT的碳排放配額,則問題(1)中的約束條件(3)調整為 (15) 同樣,生產商每周期的最優碳排放權交易數量應等于其短缺或剩余的碳排放權數量。故約束條件(15)等價于: (16) 代入到(1)中,生產商的總成本函數為: (17) s.t. (2), (4), (5), (6), (8) 從(17)中可以看出,碳排放權的周期配額CT同樣不影響生產商的決策。也就是說,當存在穩定的碳交易市場時,碳排放權配額的分配方式并不影響生產商的決策。 本文研究了一個多周期動態需求下企業生產和減排投資聯合優化決策問題,提出了一個考慮碳排放總量約束、碳排放交易和減排投資的動態批量優化模型。基于廣義Benders分解法對模型進行了分解分析,得到了最優生產決策和最優減排投資決策的一些性質,并通過數值實驗分析了碳排放配額和碳排放權價格對生產商總成本和總排放以及減排投資決策的影響。本文的研究結果揭示了配額—交易機制的幾個特點:(1)當碳交易市場上的碳排放權充足時,減少碳排放配額或改變碳排放配額的分配方式并不能影響生產商的碳排放水平;(2)碳排放權價格是影響生產商的碳排放水平和減排投資規模的關鍵因素;(3)隨著碳排放權價格的上升,即使擁有足夠的碳排放配額,生產商仍會不斷提高減排投資規模以獲得減排收益。因此,對于給定的碳排放配額,總存在一個碳排放權價格“拐點”,在此拐點價格水平之上提高碳排放權價格可以同時降低生產商總成本和碳排放水平。(4)若減少企業的碳排放配額會引起碳排放權價格的上漲,則企業從增加減排投資規模中獲得的減排收益最終會被迅速增加的碳排放成本所抵消。因此也存在一個碳排放權價格“拐點”, 在此拐點價格水平之下提高碳排放權價格可以同時降低生產商總成本和碳排放水平。這些都是在已有文獻中尚未涉及,但又對配額—交易機制的應用實踐具有重要意義的結論。 [1] Hua Guowei, Cheng T C E, Wang Shouyang. Managing carbon footprints in inventory management[J]. International Journal of Production Economics, 2011, 132(2): 178-185. [2] Benjaafar S, Li Yanzhi, Daskin M S. Carbon footprint and the management of supply chains: Insights from simple models[J]. IEEE transactions on automation science and engineering, 2013, 10(1): 99-116. [3] Absi N, Dauzère-Pérès S, Kedad-Sidhoum S, et al. Lot sizing with carbon emission constraints[J]. European Journal of Operational Research, 2013, 227(1): 55-61. [4] 胡海菊, 李勇建. 考慮再制造和產品需求可替代的短生命周期產品動態批量生產計劃問題[J]. 系統工程理論與實踐, 2007, (12): 76-84. [5] 戴道明.碳排放約束下動態定價與批量的聯合決策[J]. 合肥工業大學學報(自然科學版), 2013, 36(8): 996-1001. [6] 王明喜, 王明榮, 汪壽陽, 等. 最優減排策略及其實施的理論分析[J]. 管理評論, 2010, 22(6): 42-47. [7] 趙道致, 張學強. 面向碳減排投資優化的低碳供應鏈網絡設計及優化研究[J]. 物流技術, 2013, 32(3): 215-218. [8] 謝鑫鵬, 趙道致. 基于CDM的兩級低碳供應鏈企業產品定價與減排決策機制研究[J]. 軟科學, 2013, 27(5): 80-85. [9] 謝鑫鵬, 趙道致. 低碳供應鏈企業減排合作策略研究[J]. 管理科學, 2013, 26(3): 108-119. [10] 杜少甫, 董駿峰, 梁樑, 等. 考慮排放許可與交易的生產優化[J]. 中國管理科學, 2009, 17(3): 81-86. [11] 何大義, 馬洪云. 碳排放約束下企業生產與存儲策略研究[J]. 資源與產業, 2011, 13(2): 63-68. [12] 侯玉梅, 潘登, 梁聰智. 碳排放交易下雙寡頭企業生產與減排研究[J]. 商業研究,2013, 55(1): 176-182. [13] 陳伯成,李英杰.“考慮排放許可交易的生產優化”的補充研究[J]. 中國管理科學, 2014, 22(9):141-148. [14] Islegen O, Reichelstein S J. Carbon capture by fossil fuel power plants: An economic analysis[J]. Management Science, 2011, 57(1): 21-39. [15] Jiang Yan, Klabjan D. Optimal emissions reduction investment under green house gas emissions regulations[R]. Working paper, Northwestern University, 2012. [16] 駱瑞玲,范體軍,夏海洋. 碳排放交易政策下供應鏈碳減排技術投資的博弈分析[J]. 中國管理科學, 2014, 22(11): 44-53. [17] 王明喜,鮑勤,湯鈴,等. 碳排放約束下的企業最優減排投資行為[J]. 管理科學學報, 2015, 18(6): 41-57. [18] 陳伯成,李英杰,閆學為. 補貼及懲罰模式下的碳排放許可交易生產優化[J]. 中國管理科學, 2014, 22(SI): 774-781. [19] 周艷菊,黃雨晴,陳曉紅,等. 促進低碳產品需求的供應鏈減排成本分擔模型[J]. 中國管理科學, 2015, 23(7): 85-93. [20] Vogt-Schilb A, Meunier G, Hallegatte S. Should marginal abatement costs differ across sectors: The effect of low-carbon capital accumulation[A]. Working Paper, World Bank, 2013. [21] 魯奎, 楊昌輝, 戴道明. 能力受限批量問題的啟發式算法與CPLEX仿真優化[J]. 系統仿真學報, 2008, 20(3): 6365-6371. [22] 魯奎, 楊昌輝, 戴道明. 運輸能力受限與費用時變批量問題的拉格朗日松弛啟發式算法[J]. 系統工程理論與實踐, 2008,(10): 47-52. [23] Geoffrion A M. Generalized benders decomposition[J]. Journal of Optimization Theory and Application. 1972, 10(4):237-260. [24] Wagner H M, Whitin T M. Dynamic version of the economic lot size model[J]. Management Science, 1958, 5(1): 89-96. [25] Brahimi N, Dauzère-Pérès S, Najid N M, et al. Single item lot sizing problems[J]. European Journal of Operational Research, 2006, 168(1): 1-16. [26] Aggarwal A, Park J K. Improved algorithms for economic lot size problem[J]. Operations Research, 1993, 41(3):549-571. [27] Gade D, Kücükyavuz S. Formulations for dynamic lot sizing with service levels[J]. Naval Research Logistics, 2013, 60(2):87-101. Optimal Production and Emissions Reduction Investment Policies in a Dynamic Lot Sizing Model Under Cap-and-trade HUANG Di1,2, CHEN Jian2, ZHOU Hong3 (1.School of Economics and Management, Beijing Jiaotong University, Beijing 100044, China; 2.School of Economics and Management, Tsinghua University, Beijing 100084, China; 3.School of Economics and Management, Beihang University, Beijing 100191, China) With the establishment and development of China’s emissions trading market, the reduction of carbon emissions intensity has become a medium and long term mandatory target in companies’ production operations management. A dynamic lot sizing model is proposed to investigate the optimal production, emissions trading and abatement investment decisions of a manufacturer under cap-and-trade. At the beginning of the planning horizon, the manufacturer determines the optimal abatement investment decisions, including the timing of investment in an abatement technology and the optimal abatement capacity. In each period, the manufacturer decides the optimal emission abatement size according to the production planning. It is assumed that the abatement technology can reduce both carbon emissions and energy consumption in the production process. Based on the generalized Benders decomposition approach, the dynamic model is analyzed and some properties of the optimal solution are derived. Numerical experiments are conducted to examine the effects of emission cap and emission allowance price on the manufacturer’s total cost, total emissions level, and the optimal abatement investment decisions. It is found that: (1) when the supply of emission allowances in the market is abundant, reducing the carbon cap or changing the initial allocation rule of free emission allowances will not reduce the manufacturer’s carbon emissions level; (2) carbon emission allowance price is the key factor to control the manufacturer’s carbon emissions level and abatement capacity; (3) with the increase of carbon price, the manufacturer will expand the abatement capacity even if it has already held enough allowances to cover all its emissions. Our research provides useful managerial insights for manufacturing firms to make investment in carbon emissions abatement under the cap-and-trade system. dynamic lot sizing; abatement investment; cap-and-trade; generalized benders decomposition 1003-207(2016)04-0129-09 10.16381/j.cnki.issn1003-207x.2016.04.015 2014-06-23; 2015-12-16 國家自然科學基金資助項目(71232007, 71301082, 71471007, 71390334);中央高校基本科研業務費專項資金資助項目(2014RC032) 黃帝(1984-),男(漢族),河南南陽人,北京交通大學經濟管理學院講師,研究方向:低碳供應鏈運作管理,E-mail:huangd@sem.tsinghua.edu.cn. F253.4 A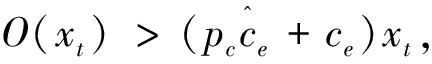

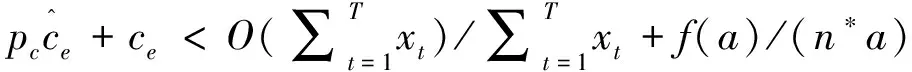
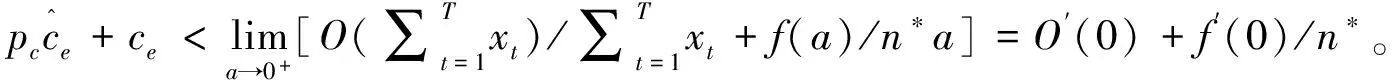
4 數值實驗與分析
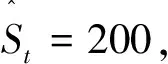


5 結語

