變分方法在時(shí)標(biāo)上一類邊值問題中的應(yīng)用?

尹 程, 蘇有慧

(徐州工程學(xué)院數(shù)學(xué)與物理科學(xué)學(xué)院，江蘇徐州 221111)

1 引言

在文獻(xiàn)[1]中，Hilger給出了一種統(tǒng)一離散分析和連續(xù)分析的新的分析理論，即時(shí)標(biāo)分析理論．因?yàn)闀r(shí)標(biāo)分析理論不但具有可以統(tǒng)一連續(xù)分析理論和離散分析理論，而且還具有可以解決那些同時(shí)包含開關(guān)和連續(xù)行為的數(shù)學(xué)模型的良好特性．所以，時(shí)標(biāo)分析理論吸引了許多學(xué)者去研究．此外，時(shí)標(biāo)分析理論還具有大量的應(yīng)用價(jià)值，這些應(yīng)用參見文獻(xiàn)[2–4]等．最近幾年，有很多文獻(xiàn)研究了時(shí)標(biāo)上動(dòng)力方程解的存在性，如文獻(xiàn)[5–9]，這些論文中所用方法主要是各種不動(dòng)點(diǎn)理論，上下界方法，重合度理論等相關(guān)知識(shí)．眾所周知，變分方法和臨界點(diǎn)理論是研究連續(xù)或者離散的邊值問題解存在性的非常重要的方法，但用變分方法研究時(shí)標(biāo)上邊值問題解存在性理論的相關(guān)論文還是較少的[10,11]，主要原因是時(shí)標(biāo)上Hilger積分加大了變分原理在時(shí)標(biāo)分析理論中應(yīng)用的難度．

為了能更好的理解變分方法和臨界點(diǎn)理論在研究時(shí)標(biāo)上邊值問題解的存在性等相關(guān)問題中的應(yīng)用，下面介紹一些相關(guān)的研究結(jié)果．在文獻(xiàn)[10]中，Agarwal等人用臨界點(diǎn)理論和變分方法研究了下述齊次Dirichlet二階邊值問題

其中u?2(t)=(u?)?(t),uσ(t)=u(σ(t))及f:T × (0,+∞) → [0,+∞)，此外，相對(duì)于每個(gè)x∈ (0,+∞),f(σ(t),x)關(guān)于任意的t在時(shí)標(biāo)T上是?-可測(cè)的，且f(σ(t),x)∈C((0,+∞))．研究者得到了邊值問題(1)存在至少一個(gè)或者兩個(gè)正解的存在性準(zhǔn)則．在不同的研究條件下，他們?cè)谖墨I(xiàn)[11]中又研究了形式如下的齊次Dirichlet邊值問題

借助于臨界點(diǎn)理論獲得了邊值問題(2)最少存在一個(gè)正解的存在性結(jié)論．

在文獻(xiàn)[10,11]的啟發(fā)下，本文研究形式如下的時(shí)標(biāo)上非自治的二階周期邊值問題

其中T是以σ(T)為周期的時(shí)標(biāo)，?代表時(shí)標(biāo)T上的導(dǎo)數(shù)，σ是向前跳躍算子．0,T∈T,σ(T)∈Tκ且f(t,x):[0,σ(T)]κT×R → R，且對(duì)任意的x∈R,f(t,x)關(guān)于任意的?-幾乎處處t∈ [0,T]Tκ是Lebesgue可積的，對(duì)每一個(gè)?-幾乎處處t∈ [0,σ(T)]κT,f(t,x)關(guān)于x連續(xù)可微．利用臨界點(diǎn)理論和變分方法，本文獲得邊值問題(3)存在至少一個(gè)周期解的存在性準(zhǔn)則．所得結(jié)果在相應(yīng)的微分方程，差分方程以及通常的時(shí)標(biāo)上都是新的．

在本文中，假設(shè)f(t,x)滿足下述條件：

(H0): 對(duì)于任意的x∈R且?-幾乎處處t∈[0,σ(T)]T，存在函數(shù)a(x)∈C(R+,R+)和b(t)∈ L1([0,σ(T)]T,R+)滿足

2 相關(guān)定義和引理

在這一節(jié)給出時(shí)標(biāo)上的一些基本定義[3,12]和相關(guān)引理．時(shí)標(biāo)上的基本特性如測(cè)度，絕對(duì)連續(xù)，Lebesgue可積和Sobolev空間等，大家可參看文獻(xiàn)[13–16]和相關(guān)文獻(xiàn)．

定義1[3]假設(shè)f:T→R,t∈Tk．如果存在一個(gè)實(shí)數(shù)θ，使得對(duì)于任意的?>0，存在t的一個(gè)開鄰域U，使得對(duì)于所有的s∈U，都有

成立，則稱f在t點(diǎn)是?-可微的，θ被稱為f在t點(diǎn)的?-導(dǎo)數(shù)，記為θ=f?(t)．若對(duì)于所有的t∈Tκ，f在t點(diǎn)都是?-可微的，則稱f在Tκ上是?-可微的．

如果T=R，則f?(t)=f′(t)；如果T=Z，則f?(t)= ?f(t)．

定義2[17]一種性質(zhì)對(duì)任意的?-幾乎處處t∈A?T或者?-幾乎處處A?T成立是說存在一個(gè)測(cè)度為0的Lebesgue?-可測(cè)子集E?A，使得這種性質(zhì)對(duì)任意的t∈AE上成立．

引理1[15]函數(shù)f2:[a,b]T→R，在[a,b]T上是絕對(duì)連續(xù)的充分必要條件是f2在[a,b)T是?-幾乎處處可微的，∈([a,b)T,R)且

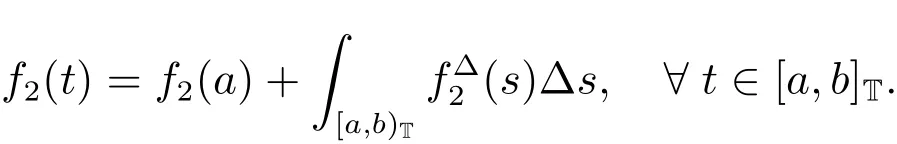
對(duì)p∈R且p≥1，設(shè)空間

主要結(jié)論的證明需要Rabinowitz在文獻(xiàn)[18]中給出的廣義山路引理．

引理6[18]設(shè)E=V⊕X，其中E為實(shí)的Banach空間，V?={0}且為有限維的．假設(shè)I∈C1(E,R)滿足(P.S.)條件以及下面條件：

(I1): 存在一個(gè)常數(shù)α和V中0點(diǎn)的一個(gè)有界領(lǐng)域D，使得I|?D≤α;

(I2): 存在一個(gè)常數(shù)β>α，使得I|X≥β．

3 主要結(jié)論

這一節(jié)，我們列出并證明二階非自治的周期邊值問題(3)周期解存在的主要結(jié)論．設(shè)

那么φ(u)是連續(xù)可微的，且

這意味著{un}是空間一個(gè)Cauchy列．根據(jù)引的緊性，可得序列{un}是空間中的收斂子列．

現(xiàn)在，列出并證明主要結(jié)論．

定理1 假設(shè)下面的條件成立：

(H1): 存在一個(gè)有界可測(cè)函數(shù)g:[0,T]T→ R滿足：對(duì)任意的x∈R及?-幾乎處處t∈[0,T]T，有

成立．那么邊值問題(3)在空間中至少有一個(gè)周期解．

證明 首先證明φ滿足(P.S.)條件．

根據(jù)(H1)，存在λ<0和M>0，使得：對(duì)任意的滿足|x|>M的實(shí)數(shù)及?-幾乎處處t∈[0,T]T，有

所以有

另一方面，根據(jù)范數(shù)的下半連續(xù)性可得

這推出了矛盾，所以假設(shè)不成立，σn}是Hiltert空間的有界數(shù)列，根據(jù)引理4，{在Hiltert空間中有收斂的子列，從而φ滿足(P.S.)條件．

其次，將證明φ在R上是逆強(qiáng)制的，也就是說

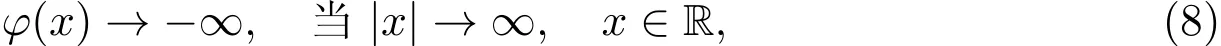
這意味著引理6中的條件(I1)被證明了．

為了證明(8)的正確性，首先證明存在δ1>0,ρ1>0，使得

這和式子(H2)矛盾，所以，(9)成立．

對(duì)任意的x∈R且|x|>ρ1，可得

從(10)–(12)可知，(8)是正確的．所以，φ在R上是逆強(qiáng)制的．

最后，證明φ在上是強(qiáng)制的，這意味著引理6的條件(I2)是成立的．

如果存在常數(shù)c?和一個(gè)序列{}?，使得∥∥→ ∞且φ()≤c?,n=1,2,···，那么，根據(jù)引理7，公式(7)，λ <0和時(shí)標(biāo)上的H¨older不等式[3]，可得

其中c3,c4,c5是正的常數(shù)，B=u(σ(t))．這跟∥un∥→ ∞矛盾，所以φ在空間內(nèi)是強(qiáng)制的．

綜上所述，引理6的所有條件都被證明了．所以，根據(jù)引理6，邊值問題(3)在Hilbert空間中至少有一個(gè)解．

4 例子

在這一節(jié)，我們給出一個(gè)例子來驗(yàn)證所得結(jié)論．設(shè)

其中n∈N,k∈Z．顯然T是以2為周期的時(shí)標(biāo)．

考慮如下的周期時(shí)標(biāo)T上的邊值問題

其中F(σ(t),uσ)=?σ2(t)uσ．容易證明(H0)定理1所有的條件成立．根據(jù)定理1可得邊值問題(13)至少有一個(gè)解．

參考文獻(xiàn)：

[1]Hilger S.Analysis on measure chains—a unifi ed approach to continuous and discrete calculus[J].Results in Mathematics,1990,18(1-2):18-56

[2]Atici F M,Biles D C,Lebedinsky A.An application of time scales to economics[J].Mathematical and Computer Modelling,2006,43(7-8):718-726

[3]Bohner M,Peterson A.Dynamic Equation on Time Scales:An Introduction with Applications[M].Boston:Birkh¨auser,2001

[4]Spedding V.Taming nature’s numbers[J].New Scientist,2003,179:28-32

[5]范進(jìn)軍，孫茂菁.時(shí)間測(cè)度上二階多點(diǎn)邊值問題正解的存在性[J].工程數(shù)學(xué)學(xué)報(bào)，2014,31(3):381-386 Fan J J,Sun M J.Existence of positive solutions to multi-point boundary value problem of second-order diff erential equations on time measure[J].Chinese Journal of Engineering Mathematics,2014,31(3):381-386

[6]Khan R A,Nieto J J,Otero-Espinar V.Existence and approximation of solution of three-point boundary value problems on time scales[J].Journal of Diff erence Equation and Application,2008,14(7):723-736

[7]Sun H,Li W T.Existence theory for positive solutions to one-dimensional p-Laplacian boundary value problems on time scales[J].Journal of Diff erential Equations,2007,240(2):217-248

[8]Wang D B,Sun J P,Guan W.Multiple positive solutions for functional dynamic equations on time scales[J].Applied Mathematics and Computation,2010,59(4):1433-1440

[9]袁曉紅，周德高，許方，等.非線性項(xiàng)帶導(dǎo)數(shù)的p-Laplacian邊值問題解的存在性[J].徐州工程學(xué)院學(xué)報(bào)，2010,25(1):1-5 Yuan X H,Zhou D G,Xu F,et al.Existence of solution of BVPs for p-Laplacian dynamic equations involving derivative[J].Journal of Xuzhou Institute of Technology,2010,25(1):1-5

[10]Agarwal R P,Espinar V O,Perera K,et al.Multiple positive solutions of singular Dirichlet problems on time scales via variational methods[J].Nonlinear Analysis,2007,67(2):368-381

[11]Agarwal R P,Espinar V O,Perera K,et al.Existence of multiple positive solutions for second order nonlinear dynamic BVPs by variational methods[J].Journal of Mathematical Analysis and Applications,2007,331(2):1263-1274

[12]Lakshmikantham V,Sivasundaram S,Kaymakcalan B.Dynamic Systems on Measure Chains[M].Boston:Kluwer Academic Publishers,1996

[13]Agarwal R P,Espinar V O,Perera K,et al.Basic properties of Sobolev’s spaces on bounded time scales[J].Advance in Diff erence Equation,2006,2006(1):1-14

[14]Aulbach B,Neidhart L.Integration on measure chains[C]//Proceedings of the Sixth International Conference on Diff erence Equations,CRC,Boca Raton,FL,2004:239-252

[15]Cabada A,Vivero D R.Criterions for absolutely continuity on time scales[J].Journal of Diff erence Equation and Application,2005,11(11):1013-1028

[16]Guseinov G.Integration on time scales[J].Journal of Mathematical Analysis and Applications,2003,285(1):107-127

[17]Rynne B P.L2spaces and boundary value problems on time-scales[J].Journal of Mathematical Analysis and Applications,2007,328(2):1217-1236

[18]Rabinowitz P H.Minimax method in critical point theory with applications to diff erential equations[C]//CBMS Regional Conference Series in Mathematics,American Mathematical Society,Providence,RI,1986

Received:07 May 2015. A ccep ted:06 Nov 2015.

Found ation item:The National Natural Science Foundation of China(11361047);the Natural Science Foundation of Jiangsu Province(BK 20151160);the Natural Science Foundation of Qinghai Province(2012-Z-910);the Six Talent Peaks Project of Jiangsu Province(2013-JY-003);the Key Project of Xuzhou Institute of Technology(2013102).

?Cor r esp ond ing author:Y.Su.E-mail address:suyh02@163.com