橡皮筋發動機

閔逸萌，高文莉，周子恒,杜　立，王思慧

(南京大學 a.匡亞明學院; b.物理學院,江蘇 南京 210093)

?

橡皮筋發動機

閔逸萌a，高文莉b，周子恒b,杜立b，王思慧b

(南京大學 a.匡亞明學院; b.物理學院,江蘇 南京 210093)

摘要：研究了通過扭轉橡皮筋作為驅動力的“發動機”的能量存儲與輸出. 根據觀察定義了橡皮筋形變的多階纏繞，在此基礎上建立模型模擬了橡皮筋解旋的能量輸出過程. 定義了該發動機的各項參量，包括總的旋轉時間、有效旋轉時間、效率等，探究了能量的分布情況. 實驗結果表明：橡皮筋發動機的大部分能量轉化為螺旋槳的動能和空氣動能.

關鍵詞：橡皮筋發動機；多階纏繞；應變能；有效旋轉時間；效率；CUPT/IYPT

本文是2014年“CUPT/IYPT”題目“Rubber Motor”的解答，原題為：經過扭轉的橡皮筋可以儲存能量，例如可以用來驅動模型飛機. 請研究該能量來源的特性，以及能量輸出隨時間變化的規律.

橡皮筋動力飛機是常見的玩具和簡易飛機模型. 本文以玩具橡皮筋飛機作為發動機模型，研究其扭轉過程中能量的存儲，以及通過釋放螺旋槳如何將應變能轉換成空氣動能、螺旋槳動能及摩擦耗散. 通過預實驗發現在扭轉圈數較大時，橡皮筋會發生多階纏繞，為此將建立了數學模型，導出了多階纏繞下存儲應變能的公式. 根據能量守恒原理，考慮螺旋槳能量釋放過程中各項功率與應變能的瞬時關系，得到了釋放過程中螺旋槳轉速隨時間變化的微分方程，從而與實驗結果做了對比.

1預實驗

為了記錄螺旋槳釋放過程中轉速的變化，采用如圖1(a)所示的裝置，先將模型飛機的“發動機”部分固定，將螺旋槳旋轉一定圈數后釋放，用高速相機(240幀/s)記錄整個釋放過程.

當初始轉動螺旋槳時，橡皮筋會卷曲并均勻纏繞，纏繞到一定圈數時，橡皮筋已經纏滿了1層. 此時如果繼續轉動螺旋槳，纏繞過一遍的皮筋將再次卷曲盤繞，稱之為二階纏繞；隨著轉動圈數的增加，還將出現三階纏繞，等等，如圖2所示. 在重復做了幾次實驗后，得到多階纏繞的數據如表1中所示. 實驗所用的橡皮筋參量為：截面2 mm×2 mm，長度30 cm，由2根并聯而成.

(a)

(b)圖1　實驗裝置

(a)一階纏繞

(b)二階纏繞

(c)三階纏繞圖2　3種纏繞情況

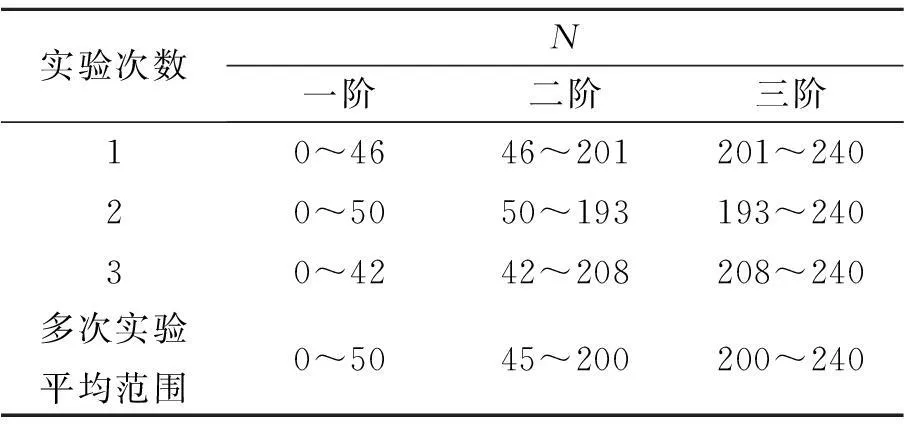
實驗次數N一階二階三階10～4646～201201～24020～5050～193193～24030～4242～208208～240多次實驗平均范圍0～5045～200200～240

旋轉不同圈數后釋放螺旋槳，此時葉片開始轉動，利用圖1中的裝置獲得轉速與時間的關系，得到的結果如圖3所示. 通過預實驗， 觀察到以下現象：

1)隨著纏繞圈數的增加，螺旋槳解旋的總時間增長.

2)隨著纏繞圈數的增加，螺旋槳的最大轉速也會增加.

3)螺旋槳具有在一段時間內保持角速度不變的狀態.

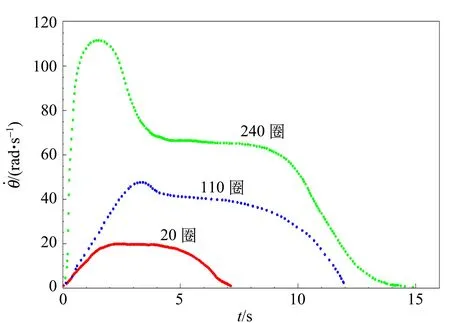
圖3　螺旋槳轉速曲線

2能量儲存與釋放的理論模型

2.1應變能與機械功

在螺旋槳被釋放前，輸入的機械功首先會以應變能的形式儲存在扭曲的橡皮筋中. 先給出這部分能量所對應的公式.

引入x,y和z方向的拉伸比λ1,λ2和λ3. 對于不可壓縮材料的單軸拉伸，有：λ1=λ和λ2=λ3=λ-0.5. 利用Mooney Rivlin模型[1]， 橡皮筋的應變能可以表示為

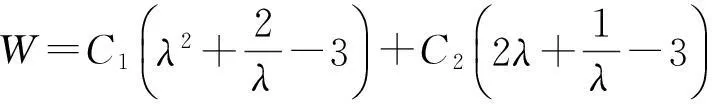
(1)

其中參量C1和C2是與材料有關的常量. 假定輸入的機械功全部轉變為橡皮筋的應變能，通過測量伸長量(拉伸比)與拉力做的功的關系[2]，由式(1)可擬合得到本實驗中C1=0.190 J，C2=0.081 J.

為了建立轉動的圈數與拉伸比λ之間的關系，建立如下模型. 假設模型發動機兩端(固定橡皮筋用)的距離是l0， 當螺旋槳轉動θ角度時，橡皮筋的長度從l0拉伸到lθ. 假設扭曲的橡皮筋可以看成是等距螺旋線，如圖4(a)所示，最終長度lθ與初始長度l0的關系如圖4(b)所示. 其中Rg是引入的有效纏繞半徑. 因此，橡皮筋的拉伸比可以表示為

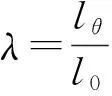
(2)

則三階纏繞的拉伸比λ可分別為

(3)

其中λi是每一階纏繞前的初始拉伸比，例如第一階纏繞，λi是橡皮筋被固定到模型飛機上的初始拉伸比. 由于僅考慮三階纏繞，根據實驗數據，取N1=50，N2=200.

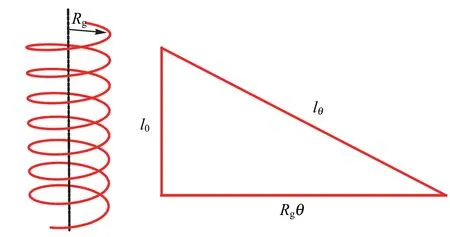
(a)　　　　(b)圖4　等距螺旋線模型及最終長度lθ和　　　初始長度l0間的關系

顯然在三階纏繞的情況下，Rg不同.Rg的值可以從實驗中獲得.

在橡皮筋發動機的能量存儲階段，輸入的機械功可以由橡皮筋的扭矩與旋轉角度(圈數)的關系推算. 通過實驗，測量得到扭矩與旋轉圈數的關系，扭矩Mf=fd， 其中d是螺旋槳的半徑，f為緩慢推動螺旋槳外端所使用的推力. 實驗中每隔5圈測量1次螺旋槳上的扭力，其測量結果如圖5所示. 圖中曲線下方的面積S與機械功成正比，即W′=2πdS. 實際計算時假設每旋進5圈的扭力不變， 那么總的輸入功可以表示為

圖5　螺旋槳旋轉的圈數N與受力f的關系

(4)

假設應變能與輸入的機械功相等，即W=W′. 由實驗測得的輸入的機械功的值可以倒推拉伸比以及有效纏繞半徑Rg的值.

2.2能量釋放與分配

當螺旋槳解旋后，橡皮筋中儲存的應變能將主要轉換成螺旋槳的動能、空氣動能及與螺旋槳軸之間的摩擦耗散. 根據能量守恒，可以得到：

(5)

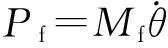
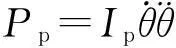
(6)

Ip為螺旋槳的轉動慣量.

Pair是螺旋槳推動空氣的功率，其形式為[3]

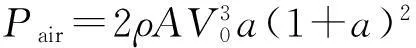
(7)

其中，ρ為來流的氣體密度，A是槳盤的面積，V0是未受螺旋槳擾動的軸向速度，對于通常的螺旋槳，a為8%～15%，取a=10%. 實驗所用螺旋槳槳葉長度為8.70 cm.

本實驗中，假設風速和螺旋槳的轉速存在線性關系，即

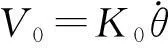
(8)

則式(7)可變為

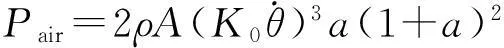
(9)

這代表了推動空氣運動對應的功率. 至此，給出了式(5)中每一項與轉速或者角位移的關系. 由實驗確定各項系數后，就可以通過求解微分方程得到解旋過程中角速度與時間的關系，并由此計算在此過程中能量的分配情況.

3實驗結果

3.1風速與螺旋槳轉速的關系

利用如圖1(b)的裝置，測量了風速與螺旋槳轉速的值，見圖6. 實驗驗證了風速和轉速之間存在線性關系，得到了比例系數K0=0.042 m/rad.

3.2解旋過程

以三階纏繞為例分析轉速隨時間的變化情況. 圖7為螺旋槳旋轉240圈后釋放的轉速隨時間的變化曲線. 顯然三階解旋的時間相對最短，在此階段中轉速以加速為主;在二階解旋過程中，轉速先下降，后趨于平穩，在相當一段時間內保持不變;最后經過一階解旋，轉速最終下降到0. 如果定義在最大速度Vmax到Vmax/e之間的時間為有效輸出時間，則有效輸出時間約10 s.

圖6　風速V0與轉速的實驗圖線

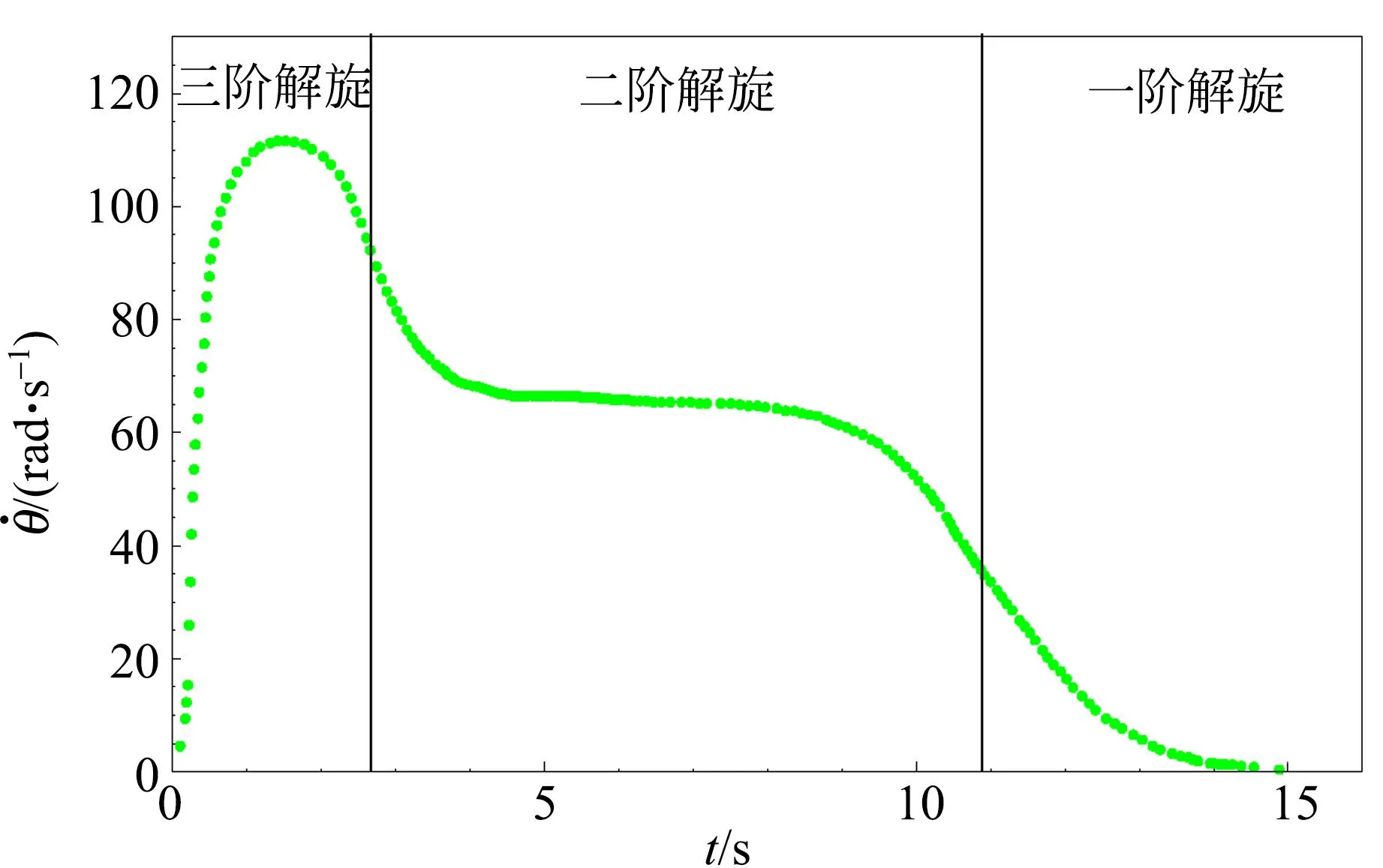
圖7　三階纏繞下的轉速隨時間的變化曲線

3.3發動機輸出性能

由于從實驗上已經得到了轉速的變化曲線，按照式(9)，容易求出空氣動能或相應功率隨時間的變化曲線，如圖8(a)所示. 實驗中螺旋槳的轉動慣量為Ip=8.56×10-5kg·m2，橡皮筋推動螺旋槳的機械功率見圖8(b)，由圖可知，在最初很短時間內(1 s左右)轉速達到極大值，橡皮筋對螺旋槳做正功，Pp>0. 此后螺旋槳減速，對外釋放能量，Pp<0.

推動空氣運動的這部分功率被視為有用功率，空氣運動的動能與輸入功相比，可以得到發動機的效率. 空氣運動的動能可以由圖8的陰影面積求得. 而總的輸入功可以從圖5中得到，即W′=∑10πdfi.

由旋槳旋轉240圈后釋放的數據，可得到總的空氣動能占輸入能量的56.6%. 多次實驗，在一階、二階和三階纏繞條件下得到的結果如表2所示，表中Pmax為最大有用功率，t總為總持續時間，t有為有效時間.

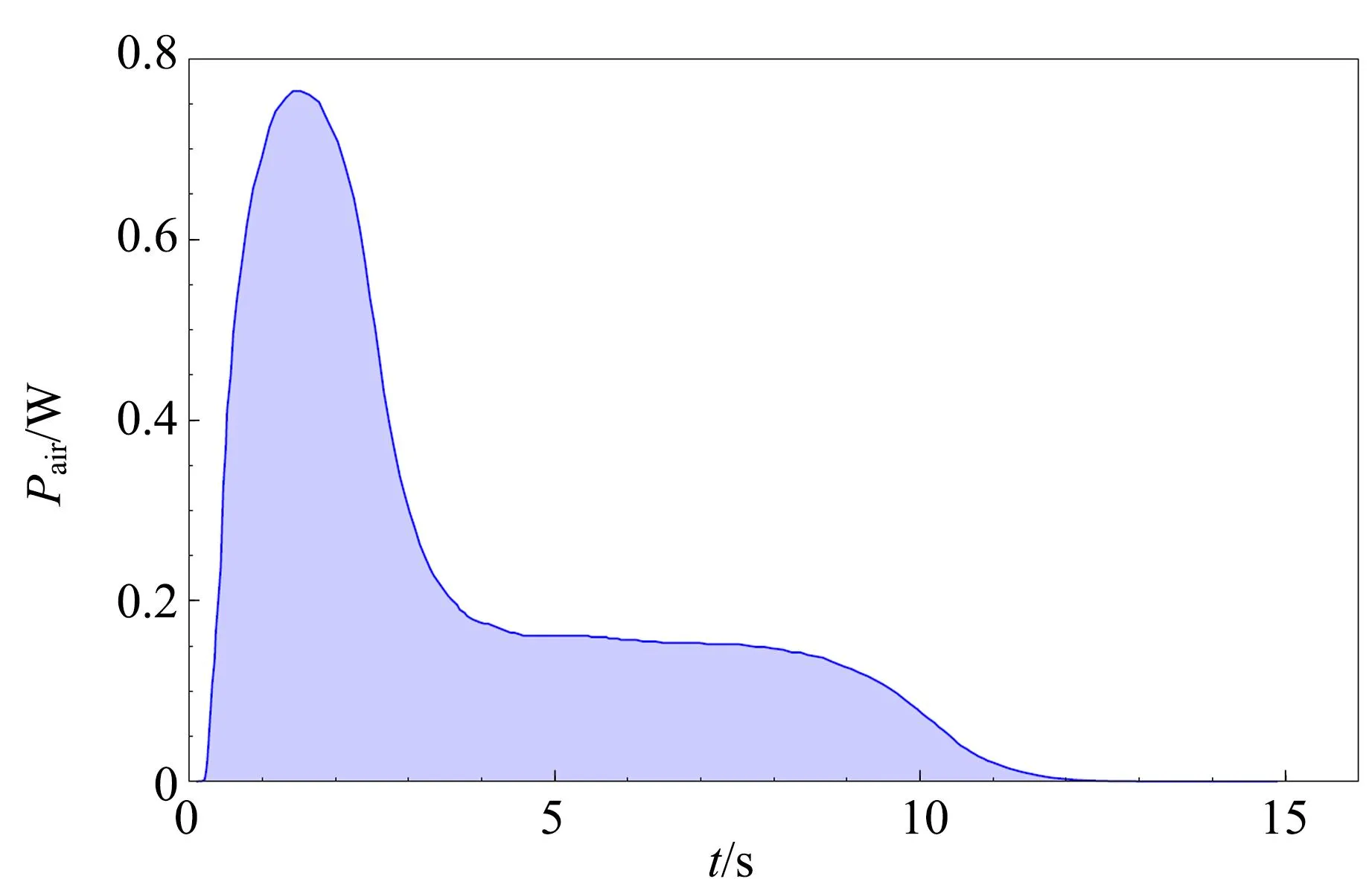
(a)

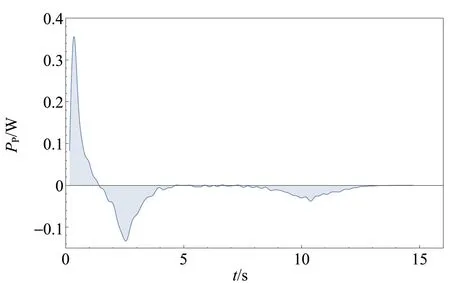
(b)圖8　推動空氣的功率以及推動螺旋槳的　　　機械功率隨時間的變化

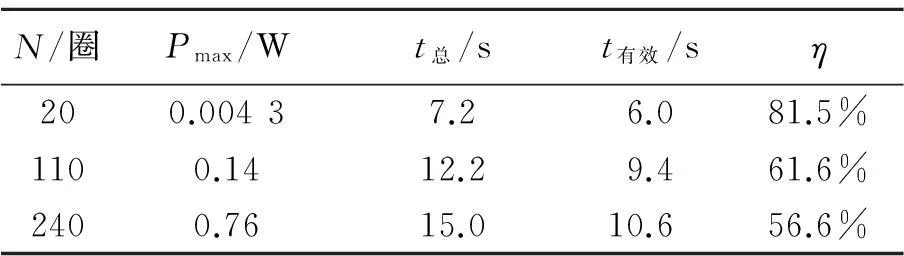
N/圈Pmax/Wt總/st有效/sη200.00437.26.081.5%1100.1412.29.461.6%2400.7615.010.656.6%

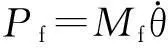
4理論與實驗對比

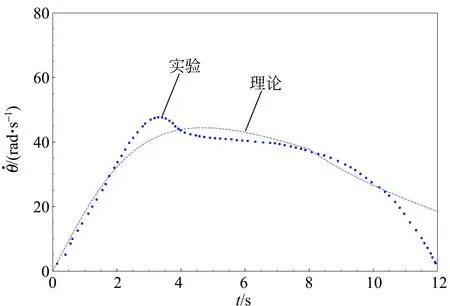
根據實驗條件確定式(5)中的各項系數后，就可以通過求解微分方程，得到解旋過程角速度與時間的關系. 通過計算得到螺旋槳在旋轉20，110，240圈后釋放的角速度與時間關系，見圖9.

(a)20圈

(b)110圈

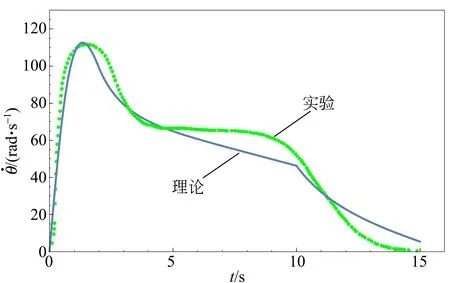
(c)240圈圖9　角速度與時間關系

經對比發現，理論結果與實驗值基本吻合，但在實驗中沒有明顯地出現轉速穩定的平臺階段 (尤其在一級纏繞中存在轉速穩定的平臺，提示模

型過于簡化，可能由于忽略了拉伸和釋放過程的非線性和摩擦導致的).

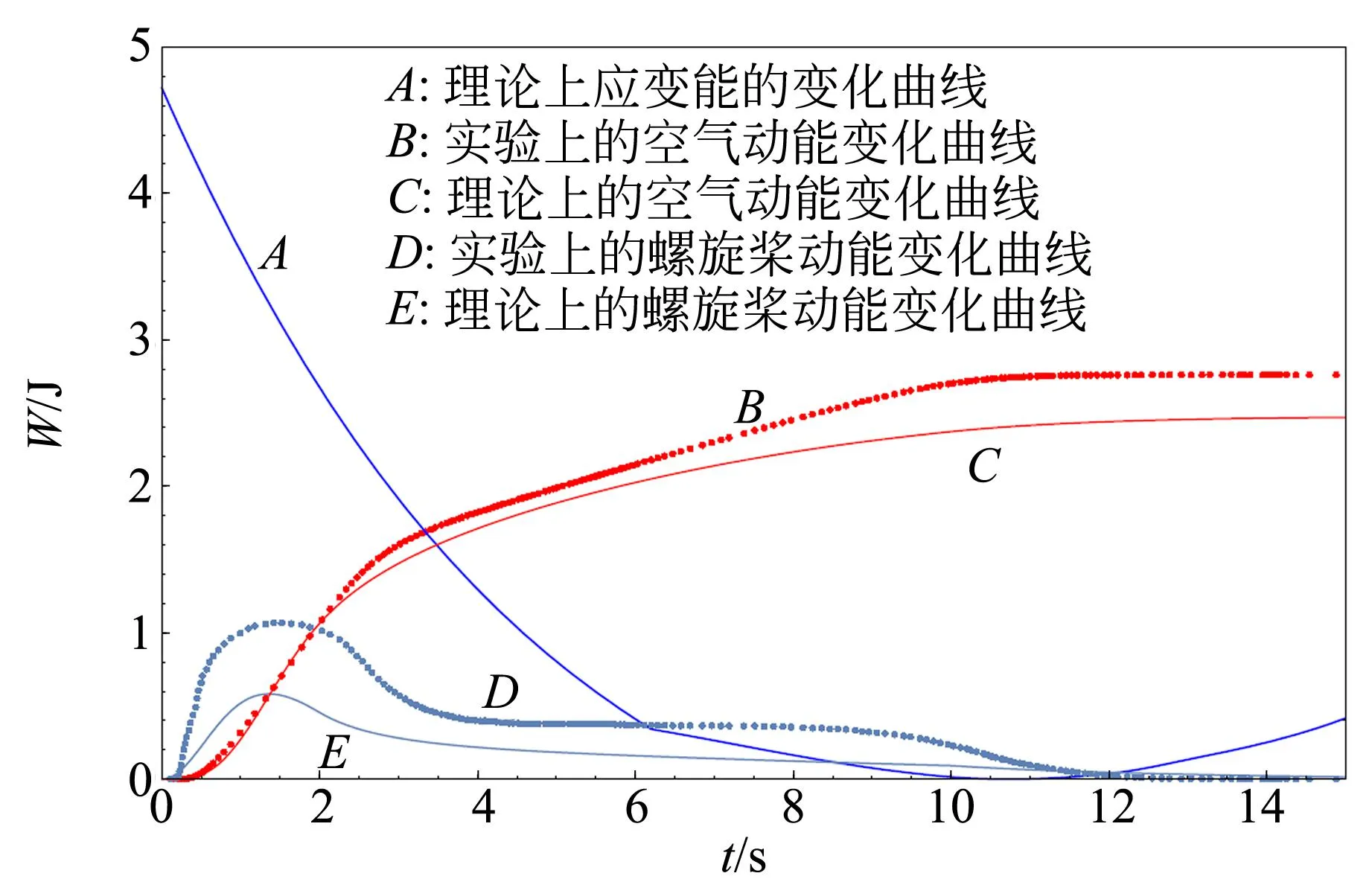
圖10　發動機能量隨時間的變化(240圈)

5結束語

研究了橡皮筋發動機性質，結合多階纏繞的實驗現象，給出了儲存應變能的公式. 經過實驗測量和理論分析，給出了螺旋槳轉速與時間的變化關系，空氣動能、螺旋槳動能以及總能量的變化情況. 定義了該發動機的各項參量，包括總的旋轉時間、有效旋轉時間、效率等. 理論模型與實驗結果對比符合較好.

致謝：感謝楊王飛同學無私的幫助和鼓勵.

參考文獻：

[1]James H M, Guth E. Theory of the elastic properties of rubber [J]. Journal of Chemical Physics, 1943,11(10):455-481.

[2]左亮，肖緋雄. 橡膠Mooney-Rivlin模型材料系數的一種確定方法[J]. 機械制造，2008,46(7)：38-40.

[3]劉沛清. 空氣螺旋槳理論及其應用[M]. 北京：北京航空航天大學出版社，2006:56-62.

[責任編輯：任德香]

Rubber band motor

MIN Yi-menga, GAO Wen-lib, ZHOU Zi-hengb, DU Lib, WANG Si-huib

(a. Kuang Yaming Honors School; b. Physics School, Nanjing University, Nanjing 210093, China)

Abstract:The properties of a rubber band motor, a toy motor that stores mechanical energy in a twisted rubber band and releases the energy through an aircraft propeller in an unwinding process, was systematically studied. The strain energy stored in the winded band was converted into three parts: kinetic energy of air, kinetic energy of propeller, frictional dissipation of propeller. For each one of them, a mathematical model was built to account for its contribution to the motor performance. Particularly, configurations of a twisted rubber band were classified into three types: the primary winding, the secondary winding and the tertiary winding. Various properties revealed by the experiment were clarified by our theory.

Key words:rubber motor; kink configurations; strain energy; effective spinning time; efficiency; CUPT/IYPT

中圖分類號：O344.1

文獻標識碼：A

文章編號：1005-4642(2016)04-0027-05

作者簡介：閔逸萌(1995-)，男，江蘇蘇州人，南京大學匡亞明學院2013級本科生.指導教師：王思慧(1964-)，女，北京人，南京大物理學院教授，博士，從事基礎物理理論與實驗教學.

收稿日期：2015-12-31