一種單自由度振動系統動態載荷識別方法

武江凱，白明生，張 永（中國空間技術研究院 載人航天總體部，北京 100094）

?

一種單自由度振動系統動態載荷識別方法

武江凱，白明生，張 永
（中國空間技術研究院 載人航天總體部，北京 100094）

摘要：航天器在飛行過程中經歷了復雜的力學環境，但是目前又無法直接測量出這種復雜力學載荷函數。針對這一問題，提出了一種應用力學載荷識別方法確定航天器所經受力學載荷的新方法，針對單自由度振動系統模型，以二次多項式為基函數，推導建立了基于Duhamel積分的動態載荷識別模型。仿真分析結果表明，該方法具有很高的識別精度，且不存在誤差積累問題。該方法為下一步試驗驗證和工程應用提供了理論基礎和技術支撐。

關鍵詞：復雜力學環境；載荷識別；Duhamel積分；二次多項式

http://www.bisee.ac.cnE-mail:htqhjgc@126.comTel:(010)68116407, 68116408, 68116544

0　引言

確定載荷的方法一般有兩種，即直接測量法與間接識別法。前者直接測量載荷本身或通過測量與載荷有關的參數確定載荷的大小。比如，為了給國際空間站開展微重力環境研究做準備，NASA曾在“和平號”空間站對航天員在艙內行走所引起的載荷進行了測量。然而在工程實際中，由于結構和載荷本身的復雜性（如運載火箭在飛行中產生的震顫、海洋平臺等大型構筑物受風浪、基礎激勵作用等），很難對作用于結構的外載荷特別是沖擊載荷進行直接測量或計算。因此，由結構的動響應和結構的動態特性來間接反演動載荷是非常必要的。

載荷識別起源于20 世紀70 年代末，因研究直升機飛行時螺旋槳主軸所受到的力等軍事用途而得以發展[1-2]。到目前為止，動態載荷識別方法主要有頻域法和時域法。頻域法提出較早、發展成熟且識別精度高，其缺點是在結構固有頻率處求解方程容易出現病態，對響應信號樣本有一定長度要求，對噪聲影響也非常敏感，只適用于穩態動載荷和隨機載荷的識別[3-4]。時域法對各種載荷識別都具有較強優勢，但目前該方法大都基于待識別載荷為一階躍載荷或Wilson-θ假設，通過建立遞推連鎖計算格式進行求解，但對采樣時間和初值都很敏感，存在累積誤差[5-8]。近年還發展了計權加速度法（SWAT）、逆系統求解法、基于神經網絡法、小波變換法等[9-10]，但都處于載荷識別初步研究階段。

本文提出一種基于單自由度振動系統的動態載荷識別方法：以二次多項式為基函數，建立基于Duhamel積分的單自由度振動系統的載荷識別模型，并通過仿真分析對模型的正確性進行驗證。

1　單自由度振動系統描述

典型單自由度振動系統如圖1所示。

圖1　單自由度振動系統Fig. 1　Single-degree-of-freedom vibration system

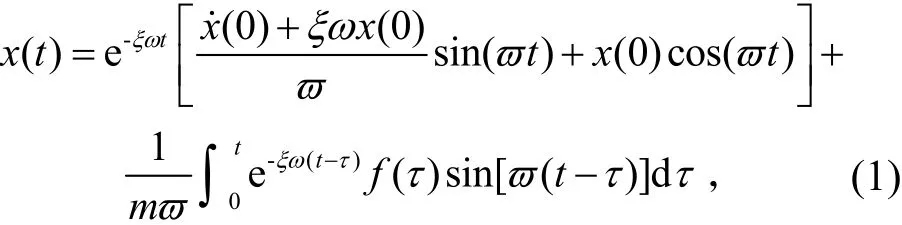
式中：x&&、x&、x分別為單自由度振動系統加速度、速度和位移信號；m、c、k分別為振動系統的質量、阻尼和剛度；為自振角頻率；為阻尼比；；x(0)、x&(0)為初始位移和初始速度；f(τ)為待識別的動態載荷[13]。

2　單自由度振動系統載荷識別方法

動態載荷識別問題，其實就是通過以上3個方程組聯立求解f(τ)的問題。由于該求解問題是一個非線性的非正定問題，對應f(τ)為一個解集，所以本文選擇二次函數f(t)=at2+bt+c作為f(τ)的基本形式，將動態載荷f(τ)的求解問題轉換為求取不同時刻參數a、b、c的問題。

動態響應的測試信號可以是動態位移、動態速度或者動態加速度等，在ti-1時刻的響應xi-1反映了在初始條件和此刻以前動態載荷綜合作用下的結果。為了減小累積誤差和消除對初始條件的敏感性，在對某一時刻動態載荷識別時，可在[ti-1, ti+1]時間段內進行，以ti-1時刻的響應為初值，即在[ti-1, ti+1]時間段內設ti-1為0時刻，由于在ti-1、ti、ti+1時刻的函數值中，ti時刻的精度最高，所以在[ti-1, ti+1]時間段內僅作fi的識別。

以ti-1時刻為初值，利用Duhamel積分求解得到ti時刻的響應為：

將載荷函數f(t)=at2+bt+c代入式(4)，則式(4)中的積分項可寫為

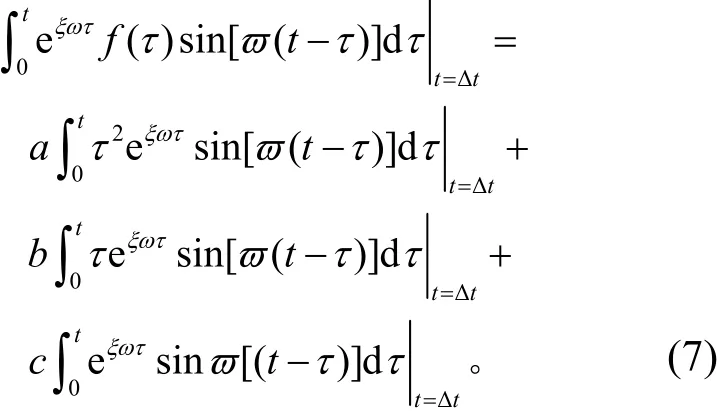
同理也可以將載荷函數代入式(5)、式(6)中的Duhamel積分項，然后對Duhamel積分參數Iu2、Iu1、Iu0、Iv2、Iv1、Iv0、Iw2、Iw1、Iw0進行如下設定：

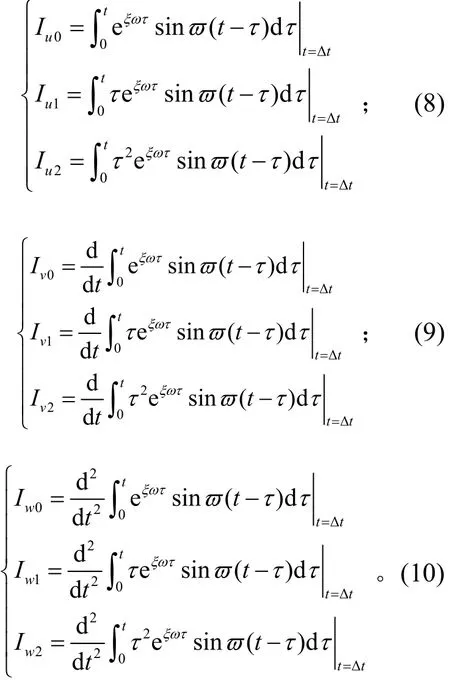
式(8)～式(10)中都有顯式結果，限于篇幅，在此處不一一列出。分別將式(8)、式(9)和式(10)代入到式(4)、式(5)和式(6)，則有：

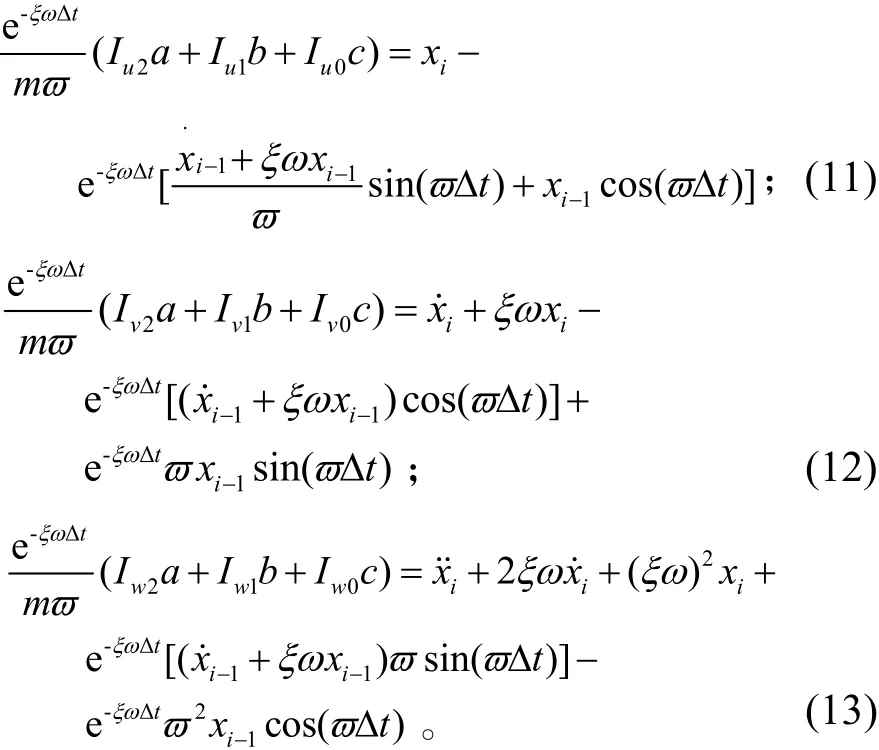
式(11)～式(13)的右端項可由ti時刻和ti-1時刻的系統位移、速度和加速度相應得到。分別令式(11)～式(13)的右端項為qi、q&i、q&i&，則可得到

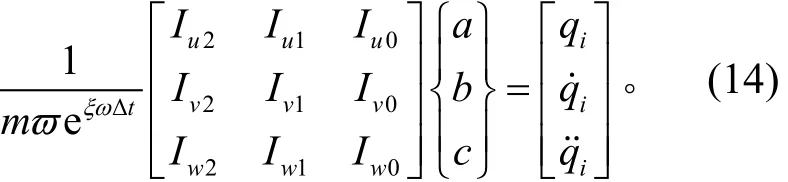
同理，分別對ti+1時刻的Duhamel積分參數Iu21、Iu11、Iu01、Iv21、Iv11、Iv01、Iw21、Iw11、Iw01進行設定，則通過對動力響應方程進行變形、簡化，可得

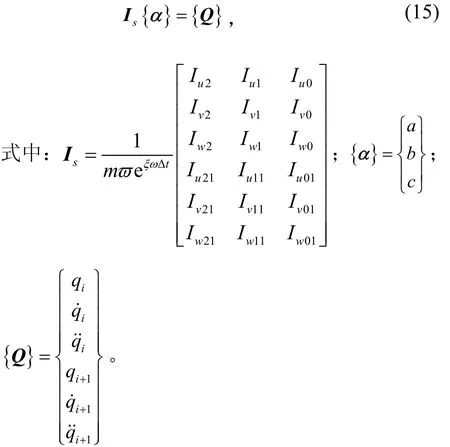
通過方程推導，將載荷識別轉化為式(15)中對{α}的求解問題。由于在信號測試中存在測量誤差和噪聲，所采用的動態載荷擬合函數與實際的動態載荷存在差異，所以，式(15)為矛盾方程組。對于矛盾方程組的求解，本文選擇構造誤差e的方程：

于是將滿足式(15)的求解問題轉化為求eTe極小值，進而轉化成求解式(16)最小二乘解[14]，即：

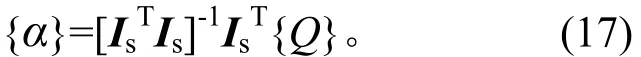
在待定參數a、b、c求得后，則可將[ti-1, ti+1]時間段內的動態載荷描述按f(t)=at2+bt+c的形式給出。但依據Gauss插值的性質，以中間點的插值精度最高，因此，在[ti-1, ti+1]時間段，取ti時刻的值為識別結果，即fi= a?t2+b?t+c，然后后移一個?t的時間間隔作下一個時刻的動態載荷識別。

3　算例仿真分析

為了驗證單自由度振動系統動態載荷識別理論的正確性，本文采用圖1所示系統對識別方法進行仿真驗證。

為不失一般性，設系統中m=1 kg；c=0.4 N·s/m；k=1 N/s；f(t)=F0sin(ωt)，F0=1 N，ω=5 rad/s，t∈[0, 20] s，分析步長Δt取為0.1 s，得到原始載荷時間歷程f(t)，如圖2所示。

圖2　原始載荷時間歷程Fig. 2　Time history of original load

依據結構動力學理論，應用Duhamel積分，單自由度系統在外界激振力作用下系統位移、速度和加速度響應如圖3所示。

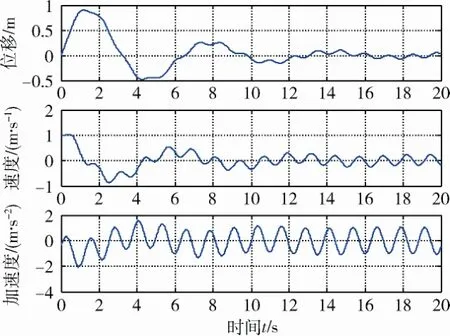
圖3　激振力作用下單自由度系統響應Fig. 3　Response of single-degree-of-freedom system with excitation force

應用本文研究的動載荷識別理論及測得的系統響應值對外加激勵載荷進行識別，識別結果及相對誤差分別如圖4和圖5所示。

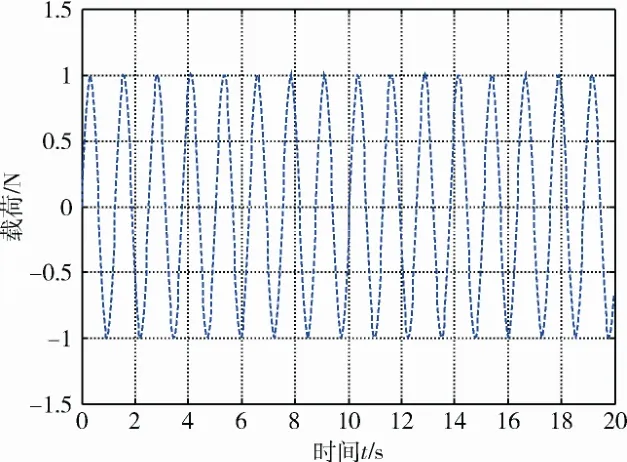
圖4　識別載荷時間歷程Fig. 4　Time history of load identification

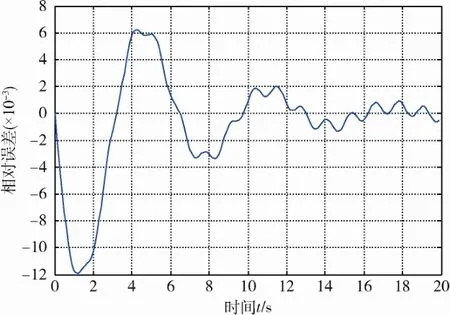
圖5　識別載荷誤差曲線（步長0.1 s）Fig. 5　Error curve of load identification(time step is 0.1 s)

從圖5可以看出：動態載荷識別穩定誤差不超過2%，且只與求解時刻及其前后時刻的振動狀態有關，而不受此前時刻載荷的影響，同時也不會對以后識別產生影響；識別過程不受初值和邊值的影響，不會帶來誤差傳遞和累積問題，即誤差不會出現擴散；識別結果都能很好地逼近原始輸入載荷，最小誤差穩定在2‰之內，說明本識別方法對測量干擾具有較強的魯棒性。

保持系統參數不變，調整分析步長Δt為0.01s情況下的系統識別誤差如圖6所示。可看出，識別精度提高了1個數量級，即系統識別精度會隨著采樣頻率的提高而提高，說明提高采樣頻率對改善載荷識別精度具有重要作用。

圖6　識別載荷誤差曲線（步長0.01s）Fig. 6　Error curve of load identification(time step is 0.01 s)

4　結束語

本文以二次多項式為基函數，基于Duhamel積分和模態分解技術推導建立了單自由度振動系統載荷識別模型，可對各種非平穩動態載荷進行實時識別，同時對樣本數據長度沒有要求；由于不進行傅里葉變換，避免了由截斷帶來的窗泄漏問題。算例仿真結果表明：該識別方法具有很高的識別精度，且不存在誤差傳遞和積累問題；提高采樣頻率對提高系統的識別精度有重要作用。

鑒于該方法的理論推導及仿真分析僅針對單自由度振動系統，且有待進一步試驗驗證，以及在復雜多自由度動態載荷識別方面還存在不確定性及局限性，因此在后續工作中有待深入研究。

參考文獻（References）

[1] Schulte H, Gerland P. A systematic load identification procedure for parallel robot manipulators[C]∥Mechanics of 21stCentury ICTAM04 Proceedings. Warsaw, Poland, 2004: 21-22

[2] Nordstrom L J L. A dynamic programming algorithm for input estimation on linear time-variant system[J]. Comput Method Appl Mech Engrg, 2006, 195: 6407-6427

[3] 胡寅寅, 率志君. 設備載荷識別與激勵源特性的研究現狀[J]. 噪聲與振動控制, 2011, 31(4): 1-5 Hu Yinyin, Shuai Zhijun. Status of study on machine’s load identification technique[J]. Noise and Vibration Control, 2011, 31(4): 1-5

[4] 智浩, 文祥榮, 繆龍秀, 等. 動態載荷的頻域識別方法[J].北方交通大學學報, 2000, 24(4): 5-10 Zhi Hao, Wen Xiangrong, Miao Longxiu, et al. Dynamic loading identification in frequency domain[J]. Journal of Northern Jiaotong University, 2000, 24(4): 5-10

[5] 趙鳳遙, 張運良, 馬震岳. 動載荷的時域識別方法及其應用[J]. 水電能源科學, 2005, 23(1): 8-11 Zhao Fengyao, Zhang Yunliang, Ma Zhenyue. Method and application of dynamic load identification in time domain[J]. Water Resources and Power, 2005, 23(1): 8-11

[6] 朱斯巖, 朱禮文. 運載火箭動態載荷識別研究[J]. 振動工程學報, 2008, 21(2): 135-139 Zhu Siyan, Zhu Liwen. Dynamic load identification on launch vehicle[J]. Journal of Vibration Engineering, 2008, 21(2): 135-139

[7] Allen M S, Carne T G. Delayed, multi-step inverse structural filter for robust force identification[J]. Mechanical Systems and Signal Processing, 2008, 22(5): 1036-1054

[8] 徐菁, 張方, 姜金輝, 等. 運用數值迭代的動載荷識別算法[J]. 振動工程學報, 2014, 27(5): 702-707 Xu Jing, Zhang Fang, Jiang Jinhui, et al. An algorithm of dynamic load identification based on numerical iteration[J]. Journal of Vibration Engineering, 2014, 27(5): 702-707

[9] 馬慶鎮. 推力終止時結構的載荷識別及瞬態響應分析[D].長沙: 湖南大學, 2014: 7-11

[10] 王慧儒, 謝曉竹, 吳淼. 基于逆傳系統法的動態載荷識別研究[J]. 裝甲兵工程學院學報, 2005, 19(3): 79-82 Wang Huiru, Xie Xiaozhu, Wu Miao. Study on the dynamic load identification based on inversion system method[J]. Journal of Academy of Armored Force Engineering, 2005, 19(3): 79-82

[11]Doyle J F. A wavelet deconvolution method for impact force identification[J]. Experimental Mechanics, 1997, 37(4): 403-408

[12]邱吉寶, 向樹紅, 張正平. 計算結構動力學[M]. 合肥: 中國科學技術大學出版社, 2009: 316-323

[13]陳祖明, 周家勝. 矩陣論引論[M]. 北京: 北京航空航天大學出版社, 1998: 175-194

（編輯：許京媛）

The danamic load identification for a single-degree-of-freedom vibration system

Wu Jiangkai, Bai Mingsheng, Zhang Yong
(Institute of Manned Space System Engineering, China Academy of Space Technology, Beijing 100094, China)

Abstract:The spacecraft is in a complicated mechanical environment, and its external load can not be measured directly. So a mechanical load identification method is proposed for spacecraft during the flight phase. Based on the Duhamel’s integration, with the second order polynomial as the base function, the dynamic load identification mode for a single-degree-of-freedom vibration system is built. The simulation results show that this method has a high identification precision and the problem of error accumulation is solved. The method can provide theoretical bases and technological supports for the test validation and engineering applications.

Key words:complicated mechanical environment; load identification; Duhamel’s integration; quadratic polynomial

作者簡介：武江凱（1987—），男，從事航天器總體設計工作。E-mail：wjk1958@126.com。

基金項目：國家重大科技專項工程

收稿日期：2015-08-17；修回日期：2016-03-04

DOI:10.3969/j.issn.1673-1379.2016.02.004

中圖分類號：V416.2

文獻標志碼：A

文章編號：1673-1379(2016)02-0136-05