幾何畫板在初中二次函數教學中的應用
姜紅
【摘要】 幾何畫板是一款優秀的教育教學軟件,適用于數學、平面幾何、物理矢量分析等. 本文首先介紹了幾何畫板軟件和二次函數的教學特征,然后探討了幾何畫板在初中二次函數教學中的應用.
【關鍵詞】 幾何畫板;二次函數;教學應用
一、幾何畫板概述
幾何畫板是最出色的教育教學軟件之一,提供了豐富而方便的創造功能,使用戶可以隨心所欲地編寫出自己需要的教學課件. 軟件提供充分的手段幫助用戶實現其教學思想,只需要熟悉軟件的簡單的使用技巧即可自行設計和編寫應用范例. 教師通過該平臺不僅可以編制數學課件,而且可以調動學生的學習主動性. 本文將重點研究幾何畫板在初中二次函數教學過程的應用.
二、幾何畫板在二次函數教學中的應用
(一)初中二次函數的教學特征
函數中,有一種多項式函數形如y = ax2 + bx + c(a,b,c是常數,a ≠ 0),最高次數是2,這種函數稱之為二次函數. 二次函數知識點總是與圖形相對應,這也是函數的特點之一,在學習二次函數的時候,一定要注重代數與幾何的雙重錘煉,做到真正的數形結合.
二次函數教學的重點在于通過畫圖像探索二次函數的性質,學生能否可以由圖像判斷函數關系或由函數關系判斷二次函數的圖像特征是二次函數教學的關鍵. 因此,二次函數的教學需要注重學生對問題的探究過程. 傳統的二次函數教學往往注重相關結論的反復運用,而這對于初中生來說,很難深層次理解二次函數各知識點之間的內在聯系. 為了彌補傳統教學的不足之處,新型的教學模式需要注重學生對二次函數知識點的探究過程. 在教學過程中通過讓學生猜想、歸納并自己總結出二次函數式與圖像的直接關系,這不僅可以加深學生二次函數知識的理解,也可以在不同程度上提高學生的數學分析能力及歸納與概括的能力.
(二)幾何畫板在二次函數教學中的應用案例
本案例主要探索二次函數y = ax2(a ≠ 0)的圖像與性質,該部分是蘇教版九年級第5章第2節第1課時的內容.
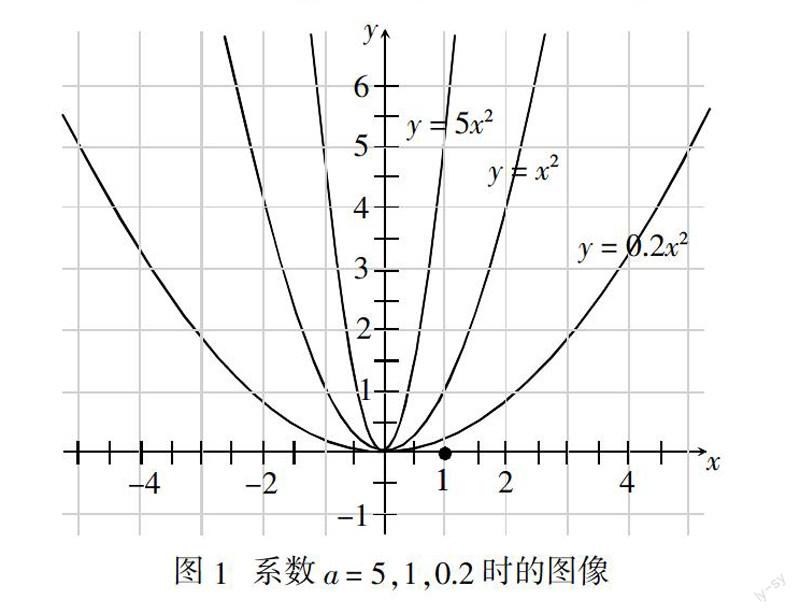
在學生初步學會畫y = x2的圖像之后,可以借助圖像,讓學生直接觀察其開口、最值以及增減性. 對于系數a取其他正數時的情況,借助幾何畫板作出y = 5x2、y = 0.2x2的圖像(如圖1). 由圖1可以總結出:當a > 0時,拋物線y = ax2開口向上,頂點在原點(0,0),是圖像最低點,
當x < 0(即對稱軸左側)時,y隨x的增大而減小;
當x > 0(即對稱軸右側)時,y隨x的增大而增大;
當x = 0時,函數有最小值,為0.
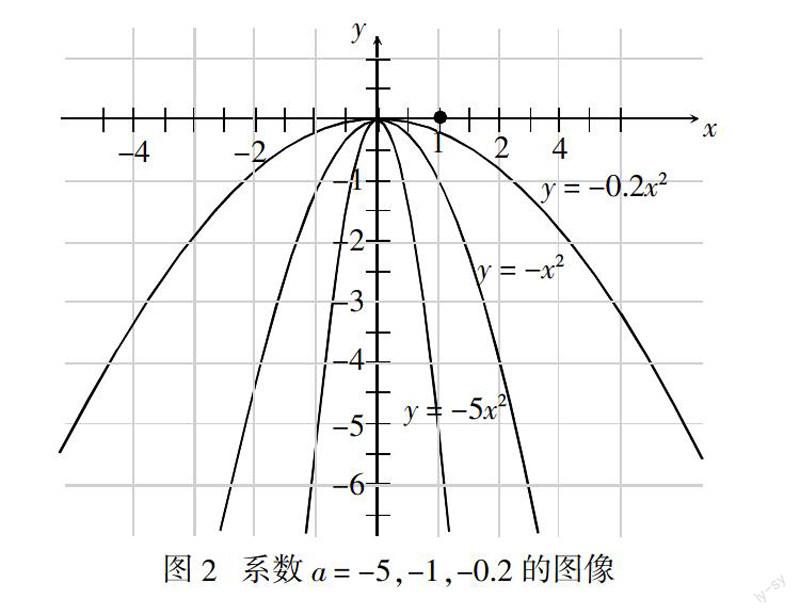
接著,對比著畫y = -x2、y = -5x2、y = -0.2x2的圖像(如圖2),由圖2可以總結出:當a < 0時,拋物線y = ax2開口向下,頂點在原點(0,0),是圖像最高點,
當x < 0(即對稱軸左側)時,y隨x的增大而增大;
當x > 0(即對稱軸右側)時,y隨x的增大而減小;
當x = 0時,函數有最大值,為0.
為了進一步探索系數a的絕對值的作用,觀察圖1和圖2可以總結出:系數a的絕對值越大,圖像越陡,拋物線開口越小;系數a的絕對值越小,圖像越平緩,拋物線開口越大;當系數a互為相反數時,圖像開口大小一樣,只是開口方向相反.
三、結束語
運用幾何畫板,在教學二次函數相關內容時,將大大提升課堂效率和容量,提升學生對圖像和二次函數性質的直觀感受. 教學實踐中適度使用,對于促進課堂質量提升,必將起著其他教學手段無法替代的重要作用.
【參考文獻】
[1]趙興文.幾何畫板在初中數學課堂教學中的應用[J].學周刊,2014(2).
[2]陳建勇.利用《幾何畫板》的測算功能解題[J].數學教學研究,2012(6).
[3]童永芳.《幾何畫板》在初中數學探究性教學中的應用[J].浙江教育技術,2014(6).
[4]張超.淺談《幾何畫板》在初中數學教學中的作用[J].基礎教育論壇,2014(4).

