基于跳擴散模型帶負債的最優資產選擇
吳安琪,舒慧生
(東華大學 理學院, 上海 201620)
基于跳擴散模型帶負債的最優資產選擇
吳安琪,舒慧生
(東華大學 理學院, 上海 201620)
摘要:構造了一個基于跳擴散帶負債的最優資產選擇模型,假設風險資產價格和累積負債的變動均由布朗運動與Poisson跳所驅動,利用均值-方差分析方法和隨機線性二次型控制理論求出最優投資組合策略和有效前沿.
關鍵詞:投資組合選擇; 跳擴散過程; 資產負債模型; 隨機線性二次型控制; 有效前沿
投資組合管理是當今金融工程中的重要研究內容,也是金融風險管理的重要技術和手段. 文獻[1]為現代投資組合理論奠定了基礎,它闡述了如何構造一個投資組合的邊界,使得在給定的風險水平下組合中的每一證券的預期收益率都達到最大化,此即為經典的均值-方差理論. 此后,均值方差框架下最優投資組合選擇的研究得到很快的發展,研究內容由最初的單周期模型推廣到多周期模型以及連續時間模型,研究方法也有很大創新. 文獻[2]采用嵌入法分析研究了多階段的均值-方差問題;文獻[3]首次引入隨機線性二次型控制方法來研究連續時間均值-方差投資組合選擇問題.
但在實際金融市場中,資產的價格過程不一定是連續過程,例如遇到重大事件突發、政策調整等問題時,股票的價格會發生大幅度的跳躍,且投資者很可能面臨負債,資產與負債的管理問題也必須考慮. 因此,這兩類問題的研究得到越來越多的關注. 文獻[4]研究了均值-方差下多階段的帶負債資產的最優投資策略和有效前沿;文獻[5]研究了在均值-方差下連續時間的資產與負債的管理問題,并采用隨機控制理論得到了最優投資策略和有效前沿;文獻[6]研究了不完備金融市場上帶有負債的投資組合選擇問題;文獻[7]研究了跳擴散過程的最優投資消費問題;文獻[8]研究了跳擴散金融市場的均值-方差投資組合選擇問題;文獻[9]研究了跳擴散市場投資組合選擇問題;文獻[10]研究了基于跳躍擴散過程的保險資金最優投資問題.
然而,現有的研究沒有既考慮資產服從跳擴散問題又考慮資產負債管理問題,實際上這兩個問題往往同時存在.源于這一情況,本文在已有研究基礎上做一推廣,研究基于跳擴散模型帶負債的最優資產選擇問題. 由于金融市場中重大信息發生的時間和產生的影響是隨機的,可以用概率空間上的Poisson過程來刻畫. 因此,本文假定風險資產的價格過程和累積負債過程均由布朗運動加Poisson跳所驅動,采用隨機線性二次型控制方法求得最優投資組合以及相應最優值函數的解析解,并利用隨機分析方法求得該最優投資組合選擇問題的有效前沿.
1問題描述
在實際的金融市場中,資產價格的變動由兩部分構成[11]:第一種變化是價格的正常波動,例如供需的暫時不平衡、經濟前景引起的變化等,這種變化可以用概率空間上的布朗運動來描述,它具有連續的樣本路徑;第二種變化是價格的不正常振動,如受到政策調整等的影響,價格會發生大起大落式的跳躍,這種變化發生的時間和產生的影響是隨機的,可以用概率空間上的Poisson過程來刻畫.
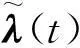
設市場上有m+1種可連續交易資產,其中一種無風險資產(債券)價格A0(t)滿足以下微分方程:
(1)
其中:α(t)為無風險資產的利率.
另外m種風險資產(股票)的價格滿足以下跳擴散隨機微分方程:
(2)

假設投資者初始資產為x0,初始負債值為l0,L(t)為投資者t時刻的累積負債值,滿足以下跳擴散隨機微分方程:
(3)
其中:μ(t)表示負債增值率;υ(t)=(υ1(t),υ2(t),…,υn(t))∈C([0,T];Rn×n)表示負債波動率;η(t)=(η1(t),η2(t),…,ηn(t))∈C([0,T];Rn×n)表示負債跳躍幅度. 上述所有方程都假定在t∈[0,T]上可測且一致有界.
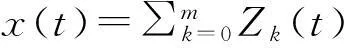
(4)
其中:
B(t)=(γ1(t)-α(t),γ2(t)-α(t),…,γm(t)-α(t))
Z(t)=(Z1(t),Z2(t),…,Zm(t))′,

由此可得
(5)
投資者希望構造一個最優的投資組合策略,使得在均值所刻畫的期望回報和方差所刻畫的風險之間達到最優的平衡. 即均值-方差框架下投資組合選擇遵從:
(6)
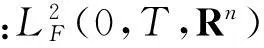

由定義可知,問題即轉為求有效前沿上的有效投資組合. 而根據標準多目標最優化理論,一個有效投資組合可以通過求解一個單目標最優化問題來獲得. 因此,上述多目標最優化問題可轉化成以下單目標最優化問題:
(7)
其中:ω>0.
由于這個目標函數在動態規劃意義下是不可分的,根據文獻[2-3]的結論,可以將其轉化為以下標準隨機線性二次型問題(輔助問題):
(8)
其中:ω>0,-∞<σ<+∞.
2最優投資組合策略求解
為了得到最優投資組合策略,類似文獻[5]的思想,先求出一般的隨機線性二次型問題的解,則基于此解即可得到所需的輔助問題的解.
2.1一般的隨機線性二次型問題
以下模型是一個一般的隨機線性二次型問題:
(9)
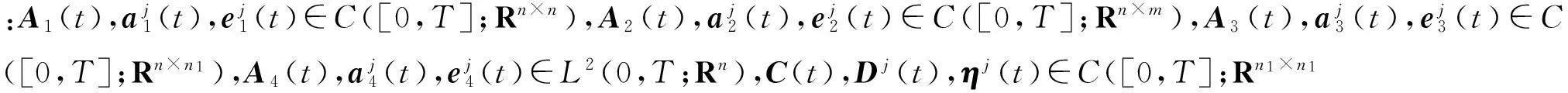
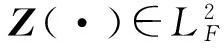
(10)
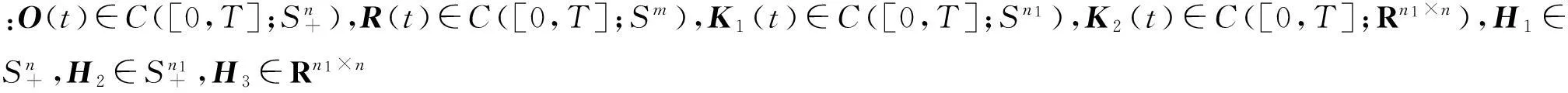
2.2跳擴散隨機線性二次型問題的解
為了求解上述隨機線性二次型問題,需要運用推廣的伊藤公式.
引理2.1[7]跳擴散過程的廣義伊藤公式.設跳擴散過程x(t)具有以下微分形式
(11)
其中:W(t)為標準布朗運動;N(t)是強度為λ的m維Poisson過程.m∈L1([0,T];R),σ,φ∈L2([0,T];Rn×n),則對任意V∈C2×1(R×R+;R)有以下等
式成立.
(12)
定義變分算子LV:R×R+→R,有
(13)
其中:M(t)是與Poisson過程N(t)相關的鞅,與W(t)相互獨立.
運用上述引理,可以得到下面這個定理,具體證明過程省略.
(14)
(15)
(16)
(17)
(18)
則隨機線性二次型問題(9)和(10)的最優投資組合策略為
Z*(t,χ,y)=-u(t)-1[ξ(t)χ+σ(t)y+θ(t)]
相應的最優值函數為
(19)
2.3輔助問題的解

對比相應的系數后,應用定理2.1,則輔助問題的最優投資組合策略為
(20)
其中:

最優投資組合策略亦可表述成總資產財富x與負債L的形式:
(21)
注:當跳躍幅度φk(t)與η(t)等于0時,模型即轉化成一般的僅由布朗運動驅動的模型,此時求出最優投資組合策略為
其中:
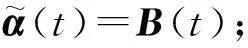
β(t)=μ(t);
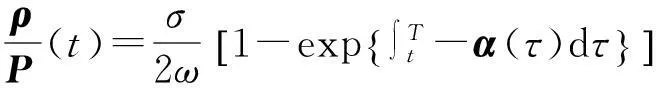
該最優投資組合策略與文獻[5]中求得的結果相一致,這也從側面印證了本文研究結果的正確性.
3有效前沿
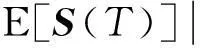
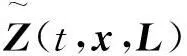
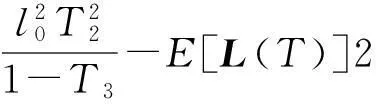
其中:
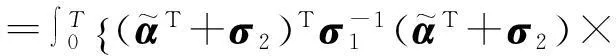
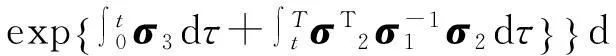
通過定理3.1很容易得到凈財富S(t)的有效前沿為
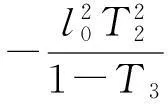
(22)
其中:
4結語
本文主要研究了均值-方差框架下,基于跳擴散模型帶負債的最優投資組合選擇問題. 采用隨機線性二次型控制方法得到了最優投資組合策略與有效前沿的解析解. 由于本文是先求出一般的隨機線性二次型問題的解,通過對比相應的系數得到實際問題的解,因此研究結果更具有一般性,便于后續進一步研究. 此外具有交易費用的跳擴散最優投資組合的選擇問題,仍值得深入探索與研究.
參考文獻
[1] MARKOWITZ H. Portfolio selection [J]. Journal of Finance, 1952, 7: 77-91.
[2] LI D, NG W L. Optimal dynamic portfolio selection: Multi-period mean-variance formulation [J]. Mathematical Finance, 2000,10(3): 387-406.
[3] ZHOU X Y, LI D. Continuous-time mean-variance portfolio selection: A stochastic LQ framework [J]. Applied Mathematics and Optimization, 2000, 42(1): 19-33.
[4] LEIPPOLD M, TROJANI F, VANINI P. A geometric approach to multi-period mean variance of assets and liabilities [J]. Journal of Economic Dynamics and Control,2004,28(6): 1079-1113.
[5] CHIU M C, LI D. Asset and liability management under a continuous-time mean-variance optimization framework [J]. Insurance: Mathematics and Economics,2006, 39(3): 330-355.[6] XIE S X, LI Z F, WANG S Y. Continuous-time portfolio selection with liability: Mean-variance model and stochastic LQ approach [J]. Insurance: Mathematics and Economics, 2008, 42(3): 943-953.
[7] JENABLANCE-PICQUE M, PONTIER M. Optimal portfolio for a small investor in a market model with discontinuous prices [J]. Applied Mathematics and Optimization, 1990, 22(2): 287-310.
[8] GUO W, XU C. Optimal portfolio selection when stock prices follow a jump diffusion process[J]. Mathematical Methods of Operation Research, 2004, 60(6): 485-496.
[9] 羅琰. 跳擴散市場投資組合研究[J]. 經濟數學,2012,29(2): 45-51.
[10] 奚曉軍. 基于跳躍擴散過程的保險資金最優投資模型研究[J].財經理論與實踐, 2013,34(185): 31-36.
[11] 趙珺. 基于跳-擴散模型的最優投資策略研究[D].南京: 南京理工大學理學院, 2010: 6.
Optimal Portfolio Selection with Liability Management and Jump-Diffusion Processes
WUAn-qi,SHUHui-sheng
(College of Science, Donghua University, Shanghai 201620, China)
Abstract:The optimal portfolio selection model with liability management and jump-diffusion processes is constructed. Assuming that the risk asset prices and the accumulated liabilities are driven by the Brownian motion and Poisson jumps, mean-variance analysis and stochastic linear quadratic control theory are used to obtain the optimal portfolio strategy and the efficient frontier.
Key words:portfolio selection; jump-diffusion process; asset-liability model; stochastic linear quadratic control; efficient frontier
文章編號:1671-0444(2016)02-0299-07
收稿日期:2014-12-29
基金項目:國家自然科學基金資助項目(60974030)
作者簡介:吳安琪(1991—),女,江西鷹潭人,碩士研究生,研究方向為概率及隨機方向. E-mail: wuanqitvxq@163.com 舒慧生(聯系人),男,教授, E-mail: hsshu@dhu.edu.cn
中圖分類號:O 211.6
文獻標志碼:A

