不同粘彈性本構模型對瀝青路面永久變形的影響分析?

李洪印

（齊魯交通發展集團有限公司，山東濟南 250101）

?

不同粘彈性本構模型對瀝青路面永久變形的影響分析?

李洪印

（齊魯交通發展集團有限公司，山東濟南 250101）

摘要：為了揭示不同粘彈性本構模型在瀝青路面永久變形數值模擬中的差異，選用兩種粘彈性本構模型表征瀝青混合料的非線性特性，基于室內單軸靜載蠕變分別獲取兩種模型的參數，運用ANSYS軟件模擬蠕變試驗過程，進而分析不同模型在數值分析中的適用性。結果表明，采用Bailey-Norton定律的非線性時間硬化蠕變模型比傳統Burgers模型更適合表征瀝青混合料高溫時的粘彈性行為，數值模擬與蠕變試驗的誤差為2.1%，小于采用Burgers模型時的誤差3.2%；且在實際應用時采用非線性時間硬化蠕變作為本構模型，輸入ANSYS軟件時更為方便，無需進行復雜的轉化，在瀝青路面車轍變形預估中的應用前景更廣闊。

關鍵詞：公路；瀝青路面；永久變形；本構模型

瀝青路面由于其無接縫、舒適性好、施工期短等優點，已成為中國高速公路的主要路面形式。當前，隨著重載交通比例和交通渠化程度的不斷提高，許多高速公路瀝青路面在遠未達到服役年限時即產生嚴重病害，如裂縫、車轍、擁包、表面松散、剝落和坑槽等，其中車轍是重載路面最主要病害形式。一般認為車轍是瀝青路面在高溫時由于面層瀝青混合料呈現顯著的粘性性質，加之受到重載交通的反復作用而產生的永久變形的累積。瀝青混合料的總變形包括瞬時彈性變形、粘彈性變形和粘性流動。在荷載作用的瞬間，由于混合料的壓縮而產生彈性形變；隨著荷載的持續作用，瀝青混合料在一定應力水平下變形不斷增加，即出現蠕變現象，反映為粘彈性變形和粘性流動。而當荷載作用的時間無限增長時，材料抗變形能力逐漸增強，即產生固結效應。另一方面，試件卸載后，其彈性壓縮立即恢復，而材料的粘彈性變形有一小部分會隨時間慢慢恢復，相當大一部分不能恢復的殘余變形最終形成車轍變形。

目前各種成熟的有限元軟件如ABAQUS和ANSYS等均開發了非線性模塊以解決瀝青路面的車轍變形模擬、車轍深度預估等問題，也有大量利用室內蠕變試驗獲取瀝青混合料粘彈性參數，然后按一定格式輸入有限元非線性模塊進行永久變形模擬的相關研究。流行的粘彈性模型有線性粘彈性本構模型如Burgers等，還有個別研究者開發了非線性模型以反映瀝青混合料的復雜流變特性。

1　常用粘彈性本構模型

根據流變學理論，將簡單力學元件如胡克彈簧、牛頓粘壺等通過并聯和串聯可形成更為復雜的組合模型，以反映瀝青混合料的粘彈性特性。常用本構模型有Maxwell模型、Kelvin模型、Burgers模型。

1.1Maxwell模型

Maxwell模型由胡克彈簧和牛頓粘壺串聯而成［如圖1（a）所示］。在應力σ作用下，彈簧、粘壺的應變分別為ε1、ε2，模型的總應變為二者之和，即：

對式（1）兩端求導，根據胡克定律和牛頓定律基本公式可得：

式（2）還可表示為：

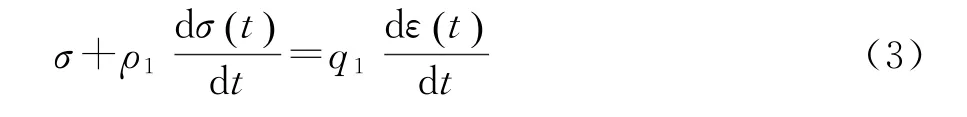
式中：ρ1=η/E；q1為導出的材料常數，q1=η。

式（3）即為Maxwell模型的本構方程。

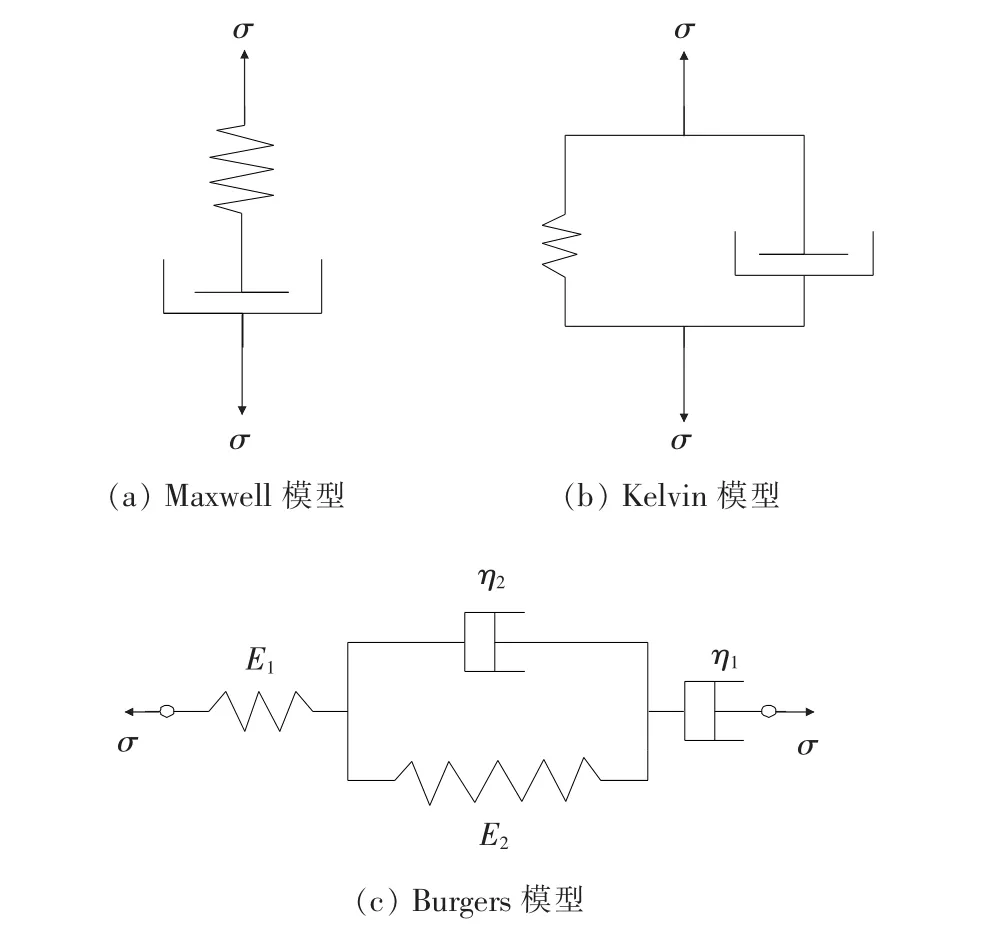
圖1　常用粘彈性本構模型示意圖

Maxwell模型中，應變被表征為隨時間的穩態流動，即變形會隨時間無限增大，且僅考慮彈性和粘性流動變形，不計粘彈性變形。此外，該模型將流動變形視作時間的線性函數，但已有研究表明瀝青路面在荷載作用下的變形具有隨時間固結穩定的趨勢，故該模型與實際情況不符。

1.2Kelvin模型

Kelvin模型由一個彈簧和一個粘壺并聯而成［如圖1（b）所示］。兩力學基本元件的應變均為ε，但總應力等于各自應力之和。其本構方程如下：

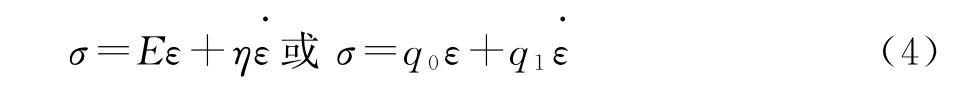
Kelvin模型無法反映材料瞬時產生的彈性變形，僅能反映其粘彈性變形，且認為卸載后變形完全恢復，這與實際情況不符。

1.3Burgers模型

Burgers模型可視作Maxwell和Kelvin模型的串聯方式［如圖1（c）所示］，是目前應用最廣的粘彈性模型。其力學特征為：在一定的應力下，兩個子模型的應力均為σ，應變分別為ε1、ε2，總應變ε為子模型應變之和。其本構方程可表示為：

式中：η1、η2、E1、E2分別為串聯、并聯粘壺及彈簧的粘度系數和彈性模量。

研究發現Burgers模型能較好地反映瀝青砼的短期粘彈性能，但該模型將混合料永久變形看作時間的線性函數，不符合瀝青混合料在實際中所表現出的長期固結效應。但由于該模型力學概念明確，分析簡單、方便，被廣泛用于各類瀝青路面永久變形的數值模擬。

2　不同本構模型在瀝青路面永久變形模擬中的適用性

為了揭示不同粘彈性本構模型在瀝青路面永久變形數值模擬中的差異，選用Burgers模型、Bailey-Norton蠕變模型表征瀝青混合料的非線性特性，基于室內單軸靜載蠕變試驗分別獲取兩種模型的參數，用ANSYS軟件模擬蠕變試驗過程，分析不同模型在數值分析中的適用性。

2.1Burgers模型

目前，在瀝青路面永久變形研究中應用較為成熟的線性粘彈性模型是Burgers模型。為了得到瀝青混合料Burgers本構模型參數，考慮兩種級配類型及外加劑情況，針對不同瀝青混合料，制備?100 mm×100 mm圓柱體試件，采用萬能試驗機進行單軸靜載蠕變試驗。為模擬高溫車轍變形，試驗溫度采用50℃，試驗前試件恒溫不少于4 h。此外，加載前用石膏對試件端部找平，并且試件兩端放置聚四氟乙烯薄片，防止端部環箍效應。加載時先對試件預加0.003 MPa應力，時間為120 s，保證壓頭與試件充分接觸，之后施加一系列壓強（0.3 MPa）3 600 s，最后卸載1 800 s。

經數據處理得出不同試件蠕變應變-時間曲線，利用蠕變試驗得到的應力-應變數據，依據式（5），借助Origins軟件進行回歸，得到不同瀝青混合料50℃粘彈性參數（如表1所示）。

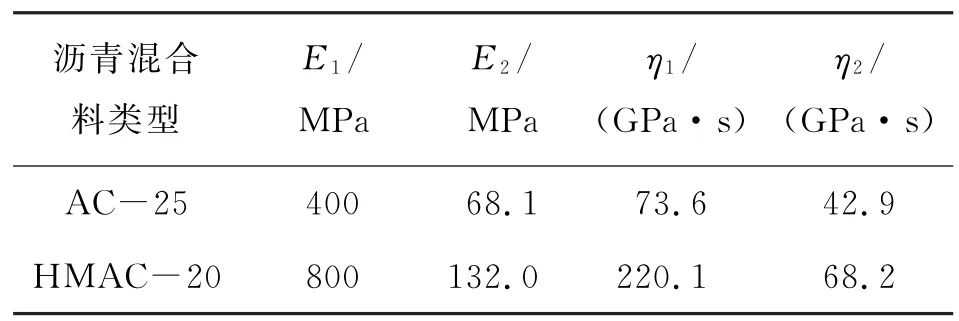
表1　不同混合料的Burgers模型參數

為了檢驗Burgers模型的適用性，利用ANSYS模擬蠕變試驗，并將模擬結果與試驗結果進行對比，結果如圖2所示。

由圖2可以看出：數值模擬結果與蠕變試驗結果大體上吻合，二者相對誤差小于3.2%。說明在ANSYS中通過輸入Prony級數形式表示Burgers模型參數進行瀝青路面永久變形模擬可行。

圖2　蠕變試驗和基于Burgers的數值模擬結果對比

2.2Bailey-Norton模型

有限元ANSYS中用于描述粘彈性材料蠕變規律的模塊共有13種，時間硬化蠕變模型為其中之一，常采用以Bailey-Norton蠕變定律表示的形式，該模型尤其適合于初始和第二階段蠕變的研究。其方程以蠕變應變率的形式表示：

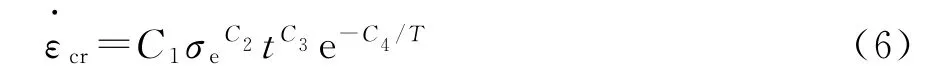
為了得到Bailey-Norton蠕變模型中的參數，采用MTS810，運用前述Burgers模型相同的方法進行蠕變試驗，得到瀝青混合料試件的蠕變應力-應變關系曲線。數據處理時，對Bailey-Norton蠕變規律進行積分處理，式（6）轉化為：

根據式（7），借助Origin多元回歸工具，得到不同混合料Bailey-Norton模型參數及擬合精度（如表2所示）。

表2　不同混合料的Bailey-Norton模型參數

為驗證該模型在瀝青路面車轍模擬中的適用性，基于試驗得到的Bailey-Norton模型參數模擬蠕變試驗過程，結果如圖3所示。

從圖3可看出：模擬結果與試驗結果吻合度較好，兩種手段下得到的蠕變應變相對誤差為2.1%。表明采用Bailey-Norton蠕變模型進行瀝青路面永久變形分析可行。此外，在實際應用時采用Bailey-Norton蠕變定律作為本構模型，輸入ANSYS軟件時更為方便，無需進行復雜的轉化。因此，該模型在瀝青路面車轍變形預估中的應用前景更廣闊。

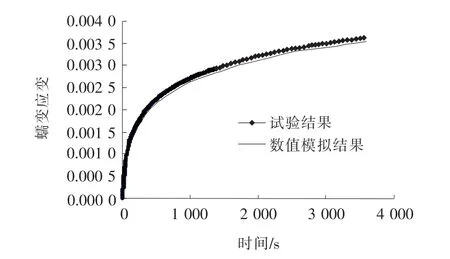
圖3　蠕變試驗和Bailey-Norton模擬結果對比

3　結語

該文選取兩種不同粘彈性本構模型分別進行室內蠕變試驗，獲取了相應模型參數，并分析了兩種模型在瀝青路面車轍變形預估中的適用性。結果表明，Bailey-Norton定律的非線性時間硬化蠕變模型比傳統Burgers模型更適合表征瀝青混合料在高溫時的粘彈性行為，數值模擬與蠕變試驗的誤差為2.1%，小于Burgers模型的誤差3.2%。且由于在實際應用時采用前者作為本構模型，輸入ANSYS軟件時更為方便，無需進行復雜的轉化，因而在瀝青路面車轍變形預估中的應用前景更廣闊。

參考文獻：

［1］ 郜玉蘭，趙隊家，韓萍，等.重載交通下山區高速公路車轍病害原因分析及對策［J］.公路，2011（1）.

［2］ 申愛琴，莊傳儀.山區高速公路瀝青路面車轍成因與防治措施［J］.筑路機械與施工機械化，2007（6）.

［3］ 李強，佘小紅，邱延峻.瀝青混凝土永久變形預測方法綜述［J］.中外公路2004，24（1）.

［4］ 張麗娟，陳頁開.重復荷載下瀝青混合料變形的粘彈性有限元分析［J］.華南理工大學學報：自然科學版，2009，37（11）.

［5］ 陳靜云，周長紅，王哲人.瀝青混合料蠕變試驗數據處理與粘彈性計算［J］.東南大學學報：自然科學版，2007，37（6）.

［6］ 徐世法，朱照宏.按粘彈性理論預估瀝青路面車轍［J］.同濟大學學報：自然科學版，1990，18（3）.

［7］ 程小亮.基于非線性蠕變方程瀝青混合料永久變形特性研究［D］.哈爾濱：哈爾濱工業大學，2010.

式中：E為彈性模型；η為粘度系數。

中圖分類號：U416.217

文獻標志碼：A

文章編號：1671-2668（2016）03-0106-03

基金項目：?山東省交通科技項目（2008Y007）；湖北省交通科技項目（鄂交科教［2013］731）

收稿日期：2016-02-03