考慮鋼筋約束效應雙裂紋砼梁的動力響應?

胡成，陳得良

（長沙理工大學土木與建筑學院，湖南長沙 410004）

?

考慮鋼筋約束效應雙裂紋砼梁的動力響應?

胡成，陳得良

（長沙理工大學土木與建筑學院，湖南長沙 410004）

摘要：在考慮縱向鋼筋約束和裂紋區(qū)應力集中雙效應的基礎上，基于Euler-Bernoulli梁理論，建立了含雙裂紋鋼筋砼梁受迫振動下的動力響應模型；運用Galerkin方法對含雙裂紋梁的動力響應方程進行分析，探討了裂紋深度、裂紋位置、裂紋間距及鋼筋約束效應對具裂紋鋼筋砼梁動力響應的影響。結果表明，分析含裂紋鋼筋砼梁的動力響應時不能忽略縱向鋼筋的約束效應，同時裂紋位置和深度等參數(shù)會對結構動力響應產(chǎn)生影響。

關鍵詞：橋梁；鋼筋砼梁；雙裂紋；受迫振動；鋼筋約束；動力響應

圖1　鋼筋砼雙裂紋梁模型

鋼筋位移模式為：

式中：us、ws分別為鋼筋在X和Z方向任意點的位移；σsxx、εsxx分別為鋼筋在X方向的應力和應變。

砼位移模式為：

式中：uc、wc分別為砼在X和Z方向的位移；σcxx、εcxx分別為砼在X方向的應力和應變；Ts為零時表示鋼筋砼梁不存在裂紋，為1時表示鋼筋砼梁存在裂紋；φj（x，z）為引進裂紋影響因子函數(shù)，沿梁軸方向表現(xiàn)出指數(shù)衰減，其形式見式（3）。

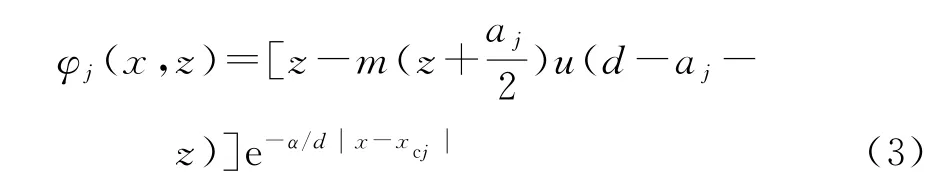
式中：aj為第j個裂紋的深度；d為半梁高；xcj為第j個裂紋所在位置；u（d-a-z）為Heaviside函數(shù)，其表達式見式（4）。

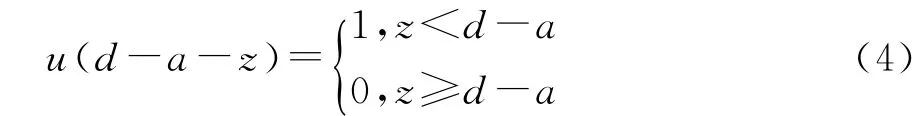
基于Hamilton能量原理建立具有多條裂紋的鋼筋砼梁的動力學控制方程，利用變分原理和邊界條件可得：

式中：δ為變分符號；T為動能；U為應變能；V為結構外力勢能；t為時間變量。

砼梁動能為：

鋼筋動能為：

式中：Vc為砼體積；ρc為砼密度；Ac為砼梁截面面積；Vs為鋼筋體積；ρs為鋼筋的密度；為受壓區(qū)鋼筋面積；為受拉區(qū)鋼筋面積。

砼部分和鋼筋部分應變能為：

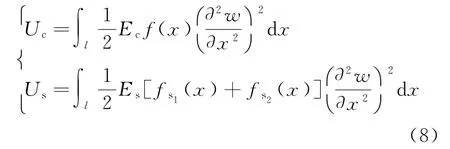
式中：Ec為砼的彈性模量；Es為鋼筋的彈性模量；的計算公式見式（9）。

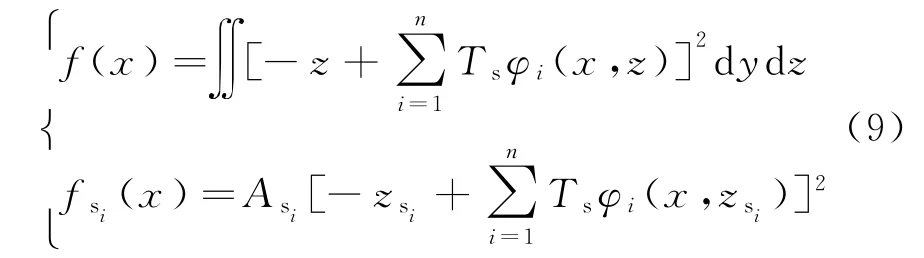
外力勢能V為：

式中：q（x，t）為分布荷載。

利用式（5）～（9）可得到含雙裂紋鋼筋砼梁受迫振動的動力學方程：

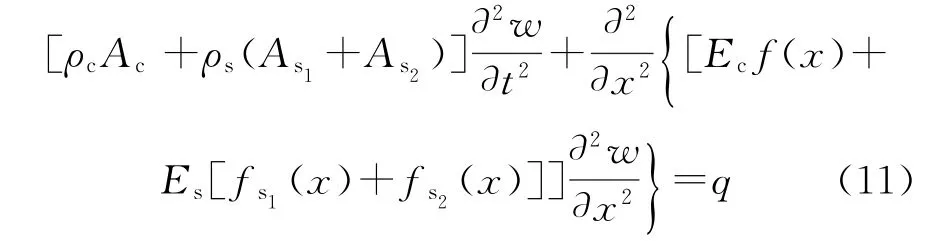
對式（10）分離變量求解，設：

將式（11）、式（12）代入式（10），可得：

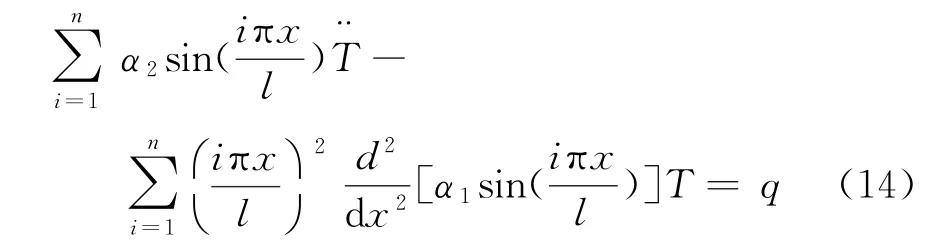
式中：

式（14）兩邊同時乘以sin（jπx/l），并沿梁長積分，可得：

將式（15）寫成矩陣的形式：

式中：T=［T1，T2，…，Tn］T為n階列向量；M為質量矩陣；K為剛度矩陣；Q為廣義力矩陣。

M、K、Q可寫成：

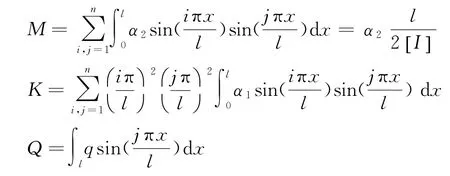
2　數(shù)值算例

以長l=6 m、高d=0.2 m、寬b=0.1 m的鋼筋砼梁為例進行分析。砼的彈性模量Ec=2.8× 104MPa，鋼筋的彈性模量Es=2.1×105MPa；砼密度ρc=2 460 kg/m3，鋼筋密度ρs=7 860 kg/m3；分別為受壓和受拉區(qū)鋼筋面積，截面面積均為158×10-2m2。

2.1鋼筋約束的影響

圖2為不同裂紋深度雙裂紋梁在跨中處作用P =8 000 N、頻率為10 Hz的正弦荷載時的動力響應。其中裂紋一位于1/4L處，裂紋二位于3/4L處，兩裂紋深度一樣。由圖2可以看出：對于含裂紋鋼筋砼梁，不計縱向鋼筋的約束效應時得到的位移響應大于計縱向鋼筋約束效應時的位移響應。表明含裂紋鋼筋砼梁的動力響應研究中不應忽略縱向鋼筋的約束效應。

圖2　不同裂紋深度時鋼筋約束對含裂紋鋼筋砼梁位移響應的影響

2.2裂紋深度的影響（對稱裂紋）

圖3為裂紋處于不同位置時含裂紋鋼筋砼梁的動力響應。圖3表明：裂紋在不同對稱位置時，隨著裂紋深度的增加，梁的位移響應增大。

2.3裂紋間距的影響

圖4為裂紋一位于1/6L處，鋼筋砼梁動力響應隨裂紋二位置變化的情況。裂紋深度a=0.05 m。從圖4可以看出：裂紋二處于3/6L時，位移響應值最大；裂紋二處于5/6L時，位移響應值最小。說明裂紋間距從2/6L增加到4/6L的過程中，隨著裂紋間距的增加，位移響應越來越小。

圖3　裂紋處于不同位置時裂紋深度對含裂紋鋼筋砼梁位移響應的影響

圖4　裂紋深度a=0.05 m時裂紋間距對含裂紋鋼筋砼梁位移響應的影響

3　結論

該文基于Euler-Bernoulli梁理論，引入應力影響因子函數(shù)，分別建立了含裂紋鋼筋砼梁中鋼筋和砼部分的能量表達式；利用Hamilton變分原理，得到了受迫振動下雙裂紋梁的動力響應控制方程，在此基礎上研究了縱向鋼筋約束效應及裂紋深度、裂紋位置、裂紋間距等參數(shù)對雙裂紋鋼筋砼梁受迫振動的影響。結論如下：

（1）考慮縱向鋼筋約束效應時含裂紋鋼筋砼梁的位移響應小于不考慮縱向鋼筋約束效應時的值，研究鋼筋砼梁時其縱向鋼筋的約束效應不應忽略。

（2）在裂紋位置不變時，具裂紋鋼筋砼梁的位移響應隨著裂紋深度的增加而增加。

（3）裂紋深度不變時，雙裂紋梁的位移響應隨著裂紋之間間距的增大而減小。

參考文獻：

［1］ 羅青松.含裂縫的預應力鋼筋混凝土梁固有頻率的有限元分析［J］.華中科技大學學報：城市科學版，2006，22（增刊2）.

［2］ 張煒，毛崎波，聶彥平.含任意數(shù)目裂紋梁的振動分析［J］.機械設計與制造，2012（10）.

［3］ Roberto Capozucca.A reflection on the application of vibration tests for the assessment of cracking in PRC/ RC beams［J］.Engineering Structures，2013，48.

［4］ 王洪霞，李學平.含表面裂紋簡支梁的非線性振動分析［J］.動力學與控制學報，2010，8（2）.

［5］ 林纓，李學平.結構多位置裂縫識別的有限元方法［J］.南京師大學報：自然科學版，2012，35（1）.

［6］ 王文亭，陳得良，劉峰.考慮鋼筋約束效應的開裂混凝土梁的自由振動［J］.長沙理工大學學報：自然科學版，2011，8（2）.

［7］ D Chen，F(xiàn) Liu.Free vibration of a single-edge cracked RC beam strengthened with FRP［J］.Journal of Engineering Mechanics，2014，140（6）.

研究中作如下假定：鋼筋砼為均質的彈性材料；應變沿著梁截面高度線性變化；裂紋微小且屬于不閉合裂紋；裂紋張開時，考慮鋼筋約束效應。

中圖分類號：U448.34

文獻標志碼：A

文章編號：1671-2668（2016）03-0161-04

基金項目：?湖南省自然科學基金資助項目（2015JJ4006）；長沙理工大學橋梁工程湖南省高校重點實驗室開放基金項目
鋼筋砼梁結構是重要的承重結構，在現(xiàn)代土木工程中應用廣泛，無論是橋梁還是建筑結構其都很重要。然而鋼筋砼結構在制造和使用過程中極易產(chǎn)生各種形式的裂紋，裂紋的存在將對結構剛度、撓度及結構穩(wěn)定性和使用壽命產(chǎn)生很大影響。為此，國內(nèi)外學者針對具裂紋砼結構的靜、動力學問題進行了深入研究。羅青松利用有限元法分析了預應力鋼筋砼一階固有頻率與鋼筋預應力大小、布筋方式、裂縫深度及裂縫位置的關系；張煒等通過遞推方法，分析了含任意數(shù)目裂紋梁在多種邊界條件下的振動問題；Roberto Capozucca對具裂紋PRC/RC梁的振動問題進行了試驗研究，并將相關試驗結果和理論分析結果進行了對比分析，研究表明砼梁材料的非均勻性和非線性對砼開裂梁的動力學特性有重要影響；王洪霞、林纓等數(shù)值模擬了簡支梁的非線性振動問題；王文亭等在考慮縱向鋼筋約束效應和裂紋區(qū)應力集中效應的基礎上，對含單裂紋鋼筋砼梁的自由振動問題進行了研究。該文基于文獻［6］～［7］，在考慮縱向鋼筋約束效應和裂紋區(qū)應力集中效應的基礎上，將相關含單裂紋鋼筋砼梁的研究成果推廣到含雙裂紋鋼筋砼梁的動力響應研究中，研究雙裂紋下鋼筋砼的位移情況及裂紋深度、裂紋位置、鋼筋約束對雙裂紋鋼筋砼梁的影響。
1考慮鋼筋約束效應的雙裂紋砼梁受迫振動方程
圖1為含雙裂紋鋼筋砼梁模型，梁長為l，梁高為2d，梁寬為2b。梁中性軸以上布置縱向受壓鋼筋，面積為As1；中性軸以下布置縱向受拉鋼筋，面積為As2。兩種鋼筋中心與中心軸的距離分別為Za1和Za2。鋼筋砼梁上存在與梁端距離分別為xc1和xc2的2條裂紋，裂紋深度分別為a1和a2。p sin（ωt）為外界受迫荷載。

收稿日期：2016-02-13