拱橋吊裝施工斜拉扣掛和勁性骨架受力分析?

李建暉，肖新輝

（1.湖南省湘西公路橋梁建設有限公司，湖南吉首 416000；2.長沙理工大學土木與建筑學院，湖南長沙 410004）

?

拱橋吊裝施工斜拉扣掛和勁性骨架受力分析?

李建暉1，肖新輝2

（1.湖南省湘西公路橋梁建設有限公司，湖南吉首 416000；2.長沙理工大學土木與建筑學院，湖南長沙 410004）

摘要：為了分析拱橋吊裝過程中斜拉扣掛索力、勁性骨架位移和穩定安全系數，以磨刀溪特大橋為工程背景，采用力矩平衡法計算分析吊裝施工過程中斜拉扣掛索力，基于有限元軟件MIDAS建立考慮施工過程的數值模型，并基于現場實測數據對模型計算數據進行驗證。研究表明，力矩平衡法能適用于拱橋勁性骨架吊裝施工過程斜拉扣掛索力的計算；隨著施工階段的累計，懸臂較小處骨架節段位移變化值較小，懸臂較大處累計位移較大；吊裝施工過程中，鋼拱圈穩定性系數逐步降低，直至懸臂最大處安全系數降至最低；勁性骨架合龍后其安全系數呈現急劇上升趨勢。

關鍵詞：橋梁；拱橋；吊裝施工；斜拉扣掛；勁性骨架；受力分析

纜索吊裝廣泛運用于鋼管砼施工中。各施工階段結構的強度和穩定性安全系數極其重要。

在吊裝拼裝過程中，預制骨架節段底部采用焊接約束，頂部采用斜拉扣掛的形式錨固，依次循環進行吊裝施工直至合龍。吊裝過程中斜拉扣掛索力是影響勁性骨架線形和成橋線形的關鍵因素之一。零彎矩法、零位移法、有限元法和力矩平衡法等常應用于扣索索力計算中。力矩平衡法因其計算簡便，同時能滿足施工精度要求，在拱橋吊裝施工中應用廣泛。吊裝過程中關鍵節點的位移控制是線形控制的另一重要因素。拱橋在懸臂吊裝狀態下骨架的穩定性遠小于合龍狀態，需對各施工階段的穩定性系數進行計算。該文以敘古（敘永—古藺）高速公路磨刀溪特大橋拱橋勁性骨架吊裝施工為工程背景，采用力矩平衡法計算斜拉扣掛索力，在此基礎上采用有限元軟件對勁性骨架關鍵點的位移進行分析計算，同時通過現場監測數據進行驗證，分析各施工階段骨架的安全系數。

1　工程概況和施工工況

磨刀溪特大橋主橋為鋼筋砼勁性骨架上承式拱橋，跨徑L=280 m，凈失跨比f/L=3.7∶1，拱軸系數m=2.2，為等高截面懸鏈線無鉸拱。采用先分段纜索吊裝勁性骨架并合龍，再澆筑砼，施工拱上立柱，最后纜索吊裝橋面系28 m小箱梁的施工方案。勁性骨架由對稱的5個節段拼裝而成，用J i表示節段編號。每個節段又分為2個小節段，用J i-j表示小節段編號。將吊裝施工工況按照勁性骨架的小節段進行編號（見圖1、表1）。

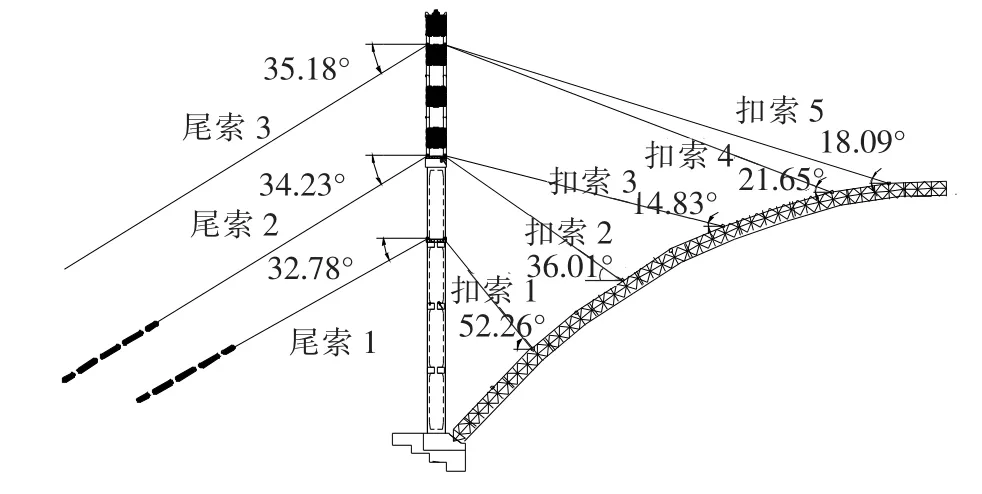
圖1　磨刀溪吊裝施工示意圖

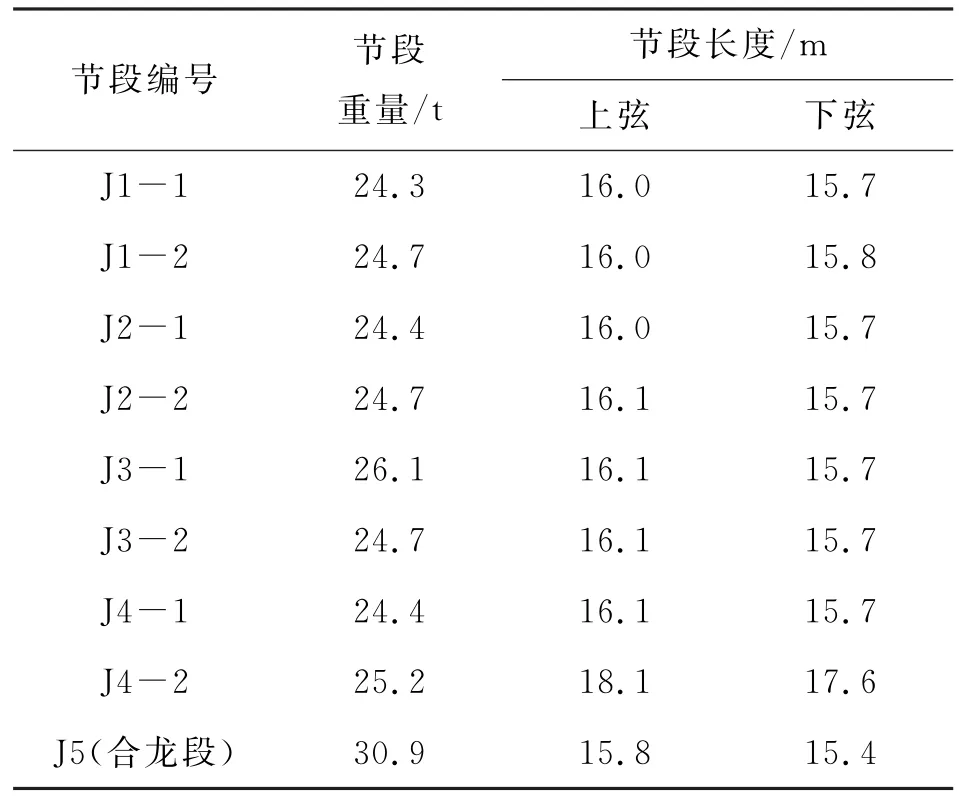
表1　吊裝節段重量及長度

2　斜拉索索力分析

力矩平衡法是在吊裝施工過程中保持鋼管拱根部力矩為零的一種簡化計算方法，索力計算見圖2。

圖2　力矩平衡法索力計算簡圖

如圖2所示，當第一節段吊裝完畢，其他勁性骨架階段尚未進行施工時，1#索只承擔第一節段的重量，對拱腳取矩，得到力矩平衡方程：

當1節段焊接完成，進行2節段吊裝施工時，1 和2節段同時受力，則2#扣索索力T2按下式計算：1#索索力受到擾動，取值將有所變化，其表達式為：

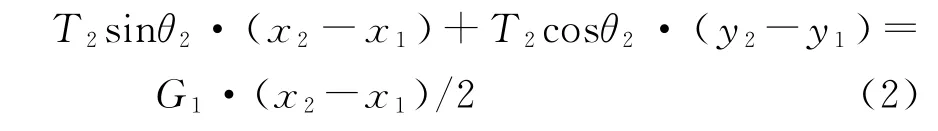
依次類推，計算后續施工工況。

吊裝過程中斜拉索索力控制精度的大小直接關系到勁性骨架安裝線形的精度和拉索施工的安全系數。采用力矩平衡法對拉索索力進行計算，各施工階段索力計算值見表2。采用振弦索力測量儀對每個施工過程進行索力監測，確保計算精度。對比分析施工現場測量值和計算索力值（見圖3），各施工階段實測索力和理論計算索力的誤差在5%以內；在工況J3-1階段，扣索1出現最大索力誤差，為-3.8%；在工況J5-1階段，扣索2、扣索3、扣索4誤差最大，分別為4%、3.2%、3.6%。

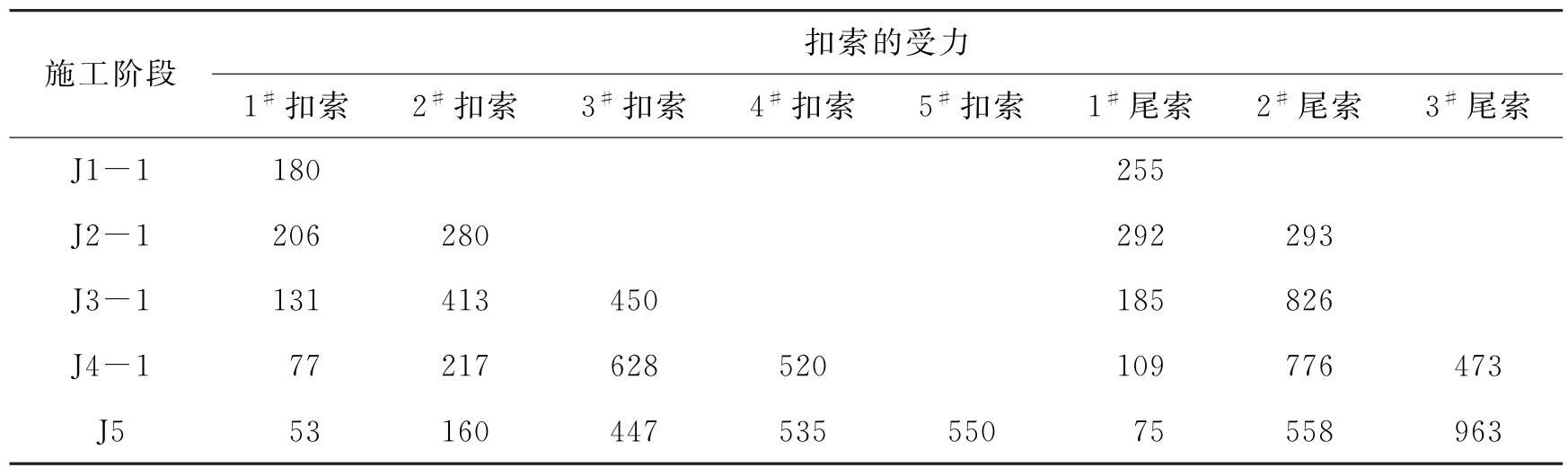
表2　扣索各工況受力　k N

圖3　不同施工工況扣索索力誤差

3　吊裝階段勁性骨架位移和穩定性分析

3.1勁性骨架位移分析

精確求解勁性骨架吊裝階段關鍵截面的位移值，能為拱橋施工提供施工預抬值，確保拱橋拱圈的線形與設計線形貼合。

采用有限元軟件MIDAS/Civil建模，全橋節點、單元分別為813和881個。采用梁單元模擬主拱圈和上部結構、桁架單元模型扣鎖和尾索，分9個細部施工階段模擬勁性骨架吊裝施工全過程。有限元模型見圖4。選取勁性骨架節段與節段焊接位置為位移關鍵點，用yji表示。需說明的是，勁性骨架受斜拉扣索和其自重共同作用，關鍵點位移有可能出現正位移（z方向向上）和負位移（z方向向下）。

為驗證各施工階段位移計算值的準確性，在各階段端部焊接棱鏡頭，觀測各施工工況關鍵截面的位移值。結果見圖5、表3。

由表3可知：隨著施工階段的累加，關鍵點yj1-1和yj2-1的位移呈現正增長趨勢，造成該現象的因素為斜拉索的增加，索力大于骨架重力。而關鍵點yj3-1、yj4-1和yj5-1下撓趨勢明顯，主要原因為施工階段懸臂過長，骨架自身出現下撓變形。通過位移監測對比模型數據，兩者之間誤差在5 mm以內，證明模型計算準確。

圖4　磨刀溪有限元模型

圖5　J5-1階段勁性骨架位移云圖

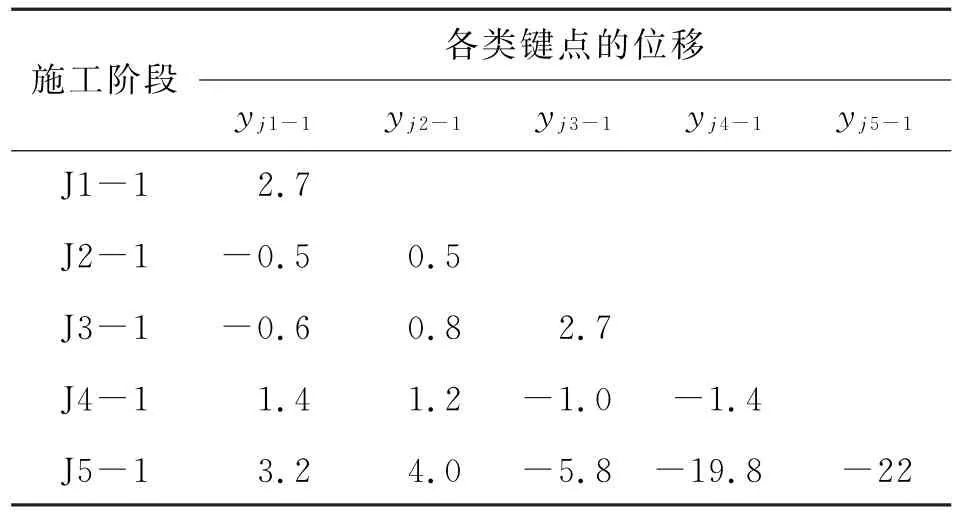
表3　各施工階段的位移值　mm

3.2穩定性分析

結構的穩定性是確保施工安全的重要方面，在最不利工況下結構的穩定性也需進行相應的驗算。不論拱端的約束情況、拱軸線選取什么樣的形式，求解拱的臨界軸壓力可近似歸結為求拱的計算長度的問題。參照中心受壓桿臨界荷載計算公式，拱的臨界壓力（拱四分點截面處的臨界軸壓力）表達式為：

式中：［N］為臨界荷載；E為拱圈剛度矩陣；I為慣性矩；S0為拱軸線計算長度的一半。

對于復雜的鋼管砼結構，由于其桿系結構復雜，很難手動建立其剛度矩陣。通過在有限元平臺建立其荷載和剛度矩陣，對其進行屈曲分析。

穩定性安全系數表達式為：

式中：N為勁性骨架所受的拱軸方向的作用荷載。

計算得各施工階段骨架安全系數分布見圖6。

圖6　施工階段骨架安全系數分布

由圖6可知：在吊裝階段，J1-1～J5-1纜索的安全系數維持在一個較高且穩定的狀態；隨著施工階段的持續累加，鋼拱圈穩定性系數逐步降低，直至合龍前J5-1工況安全系數降至最低（為4.2）；勁性骨架合龍后其安全系數呈現急劇上升的趨勢，合龍后勁性骨架安全系數為10.2。

4　結論

該文以磨刀溪特大橋拱橋勁性骨架吊裝施工為工程背景，對斜拉扣掛索力、勁性骨架關鍵點的位移、穩定性系數進行分析和計算，得到以下結論：

（1）力矩平衡法適用于拱橋吊裝過程中斜拉扣掛索力計算，具有計算簡便和準確的優點。

（2）勁性骨架吊裝施工位移分析和位移監測能為相似跨徑拱橋施工提供預抬值參考。

（3）吊裝施工過程中，鋼拱圈穩定性系數逐步降低，直至懸臂最大處安全系數降至最低；勁性骨架合龍后，其安全系數呈現急劇上升的趨勢。需高度關注最大懸臂施工階段骨架的穩定性。

參考文獻：

［1］ 何雄君，陳巧生.鋼管混凝土拱橋主拱鋼管纜索吊裝扣索索力調整［J］.武漢交通科技大學學報，1999，23（5）.

［2］ 牛潤明，安蕊梅.大跨度鋼管混凝土拱橋拱肋分段纜索吊裝模擬結構分析［J］.鐵道標準設計，2004（10）.

［3］ 李睿，楊智本，高建波.高效低價的鋼管混凝土拱橋吊裝施工方法的研究［J］.華東交通大學學報，2007，24 （1）.

［4］ 周棟梁，華強.大跨度拱橋吊裝施工線形控制研究［J］.鐵道科學與工程學報，2009，6（6）.

［5］ 周水興，江禮忠.拱橋節段施工斜拉扣掛索力仿真計算研究［J］.重慶交通大學學報：自然科學版，2000，19（3）.

［6］ 秦斌.拱橋斜拉扣掛施工中的扣索索力優化研究［D］.重慶：重慶交通大學，2011.

［7］ 周葉軍.懸臂澆筑鋼筋混凝土拱橋最優扣索索力計算方法研究［D］.成都：西南交通大學，2008.

［8］ 周水興，張敏，周建庭.鋼管砼拱桁架架設斜拉扣索最優扣點探討［J］.重慶交通大學學報：自然科學版，2000，19（4）.

［9］ 張玉平，李傳習，董創文.“零彎矩法”應用于斜拉扣掛索力確定的討論［J］.交通科學與工程，2004，20（1）.

［10］ 陳得良，繆莉，田仲初，等.大跨度橋梁拱肋懸拼時扣索索力和預抬量計算［J］.工程力學，2007，24（5）.

［11］ 田軍偉.大跨度鋼管砼拱橋拱肋吊裝施工控制［J］.公路與汽運，2012（1）.

式中：x1、y1分別為索T1扣點的橫坐標和縱坐標。

中圖分類號：U448.22

文獻標志碼：A

文章編號：1671-2668（2016）03-0169-03

基金項目：?橋梁結構安全控制湖南省工程實驗室（長沙理工大學）開放基金資助項目

收稿日期：2016-01-16