新課程背景下的初中數(shù)學創(chuàng)新教學模式研究

胡劍鋒

【摘要】新課程改革下，對初中數(shù)學的教學模式有一定的要求，改變傳統(tǒng)的教學模式，大力發(fā)展創(chuàng)新性教育，本文主要探討在新課程背景下對初中數(shù)學的教學創(chuàng)新模式的研究，并且以二次函數(shù)為例子進行教學分析。

【關鍵詞】新課程 初中數(shù)學 創(chuàng)新模式 《二次函數(shù)》

【中圖分類號】G633.6 【文獻標識碼】A 【文章編號】2095-3089（2016）10-0053-01

初中數(shù)學的難度大大加深，在教學中要不僅讓學生學習到知識，還要提高學習的興趣。在新課程標準的要求下，對初中數(shù)學的教學模式進行創(chuàng)新，教師在教學中要運用新的教學觀念進行教學，以二次函數(shù)的教學為教學案例，充分體現(xiàn)創(chuàng)新的教學方法。

1.初中數(shù)學教學模式的創(chuàng)新要求

在初中數(shù)學的教學模式中，要運用創(chuàng)新的教學方法，必須要有一定專業(yè)的培訓教師，教師要轉變傳統(tǒng)的教學觀念，在教學中要鼓勵學生，增強學生的自信心。教師要堅持自主編寫教學方案，要牢牢地把握好教學理念。在創(chuàng)新教學的模式中，學生也相應的改變傳統(tǒng)的心態(tài)，學生自主學習，并且能培養(yǎng)和探索出一定的學習方案。創(chuàng)新教學模式在實施的過程中，教師在堅持創(chuàng)新的理念同時，要結合學生的學習特點，針對實際情況進行教學，通過對教學案例的講解和分析，可以加強對不同學生的培養(yǎng)，提高學生的學習興趣和教師的教學質量。

2.以《二次函數(shù)》為教學案例運用創(chuàng)新模式

2.1二次函數(shù)的概念

二次函數(shù)是初中數(shù)學中比較重要的概念，二次函數(shù)的概念比較抽象。在數(shù)學教學中把y=ax^2+bx+c（其中a，b，c是常數(shù)，a≠0）這種形式的函數(shù)叫作二次函數(shù)。一般情況自變量x與因變量y之間存在有以下幾種關系，一般式：y=ax^2+bx+c（a≠0，a、b、c為常數(shù)），則稱y為x的二次函數(shù)。頂點式：y=a（x-h）^2+k；交點式（與x軸）：y=a（x-x1）（x-x2）。二次函數(shù)的圖像是一條主軸平行于y軸的拋物線。如果令二次函數(shù)的值等于零，則可得一個二次方程。該方程的解稱為方程的根或函數(shù)的零點。

教師對二次函數(shù)的圖像的概念，性質、方程關系、函數(shù)圖像等知識，給學生講解。因為二次函數(shù)的只是概念比較抽象，所以學生在學習中會比較吃力，教師運用創(chuàng)新的教學模式，進行教學，提高學生學習數(shù)學的興趣，提高教師講課的質量。

2.2運用創(chuàng)新教學模式的具體過程

在初中教學的二次函數(shù)是比較重要的概念，二次函數(shù)的單調性在實際生活中應用的比較多，本文選擇二次函數(shù)y=ax2 ，運用創(chuàng)新的教學模式進行教學。

教學案例：已知二次函數(shù)f（x）=1/2x2+4x+6

（1）求出該二次函數(shù)與X軸的交點的坐標。

（2）該二次函數(shù)時候有最值，求出該二次函數(shù)的最大值和最小值，并且求出該二次函數(shù)的自變量的X的值。

（3）求該二次函數(shù)是否有對稱軸，若有對稱軸，對稱軸在哪個位置上？

教學案例中的第一個問題，要求二次函數(shù)的與x軸的交點的坐標。學生在做題之前，教師首先要引導學生在會議之前學習二次函數(shù)的基本概念和性質。第一個問題是比較簡單的問題，同時也能為解決后面兩個問題提供了條件。

在對此二次函數(shù)案例教學時，首先學生應該獨立自主的解決問題，教師在檢驗，第一個問題學生基本上都能做出來，求與X軸的交點，當y=0時，代入二次函數(shù)中，得出x的解分別為-2，-6。所以該二次函數(shù)與X軸有兩個交點，交點的坐標分別為（-2，0），（-6，0）。

教師在講解第二個問題之前，首先讓學生提出自己的觀點，并且提出自己的解題思路和答案。然后教師在給學生講解該題目，最后及時對學生的解題方法進行評價。教師不能直接把解題的方法交給學生，教師在教學中充分發(fā)揮引導的作用，首先向學生提問，求二次函數(shù)的最值時，應該把二次函數(shù)進行配方，該題目中的二次函數(shù)配方之后的結果為f（x）=1/2（x+4）2-2，得出該方程式之后，進行分析該二次函數(shù)是否有最值，因為任意變量x屬于R，所以存在（x+4）2大于或者等于0 ，所以函數(shù)f（x）大于等于-2，而且當自變量為-4時，f（x）的值是-2 ，所以函數(shù)存在最值，該二次函數(shù)有最小值沒有最大值，當自變量的值為-4時，該二次函數(shù)的最小值為-2 。

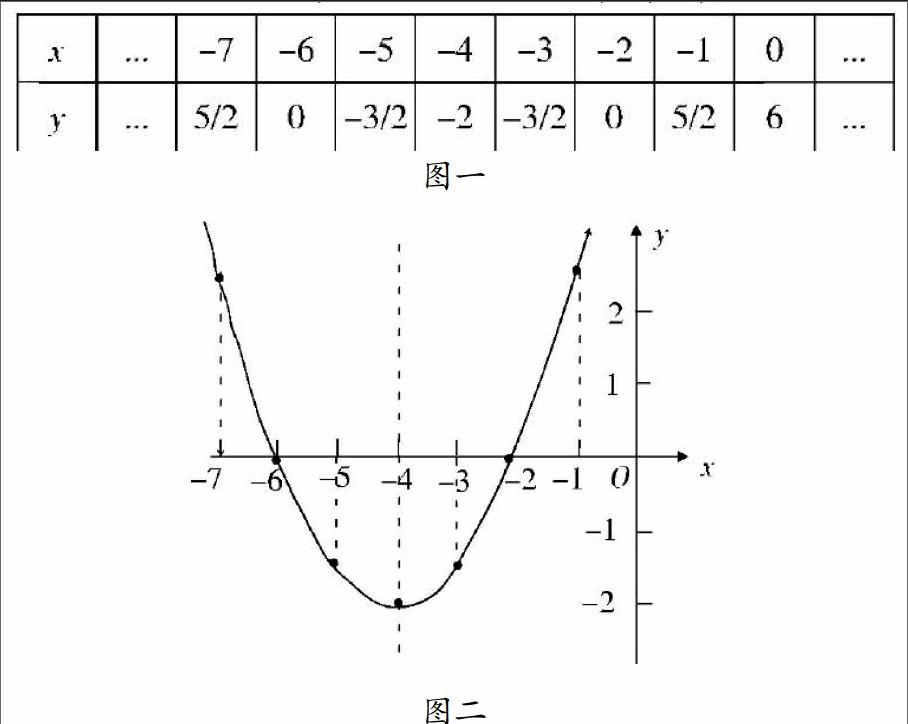
教師在講解該教學案例時，把第三個問題作為重點問題，在講解之前，把該題作為探究題，讓學生分組討論分析，然后提出自己的個體觀點和思路，教師在教學中發(fā)揮的是引導作用，引導學生自主學習和探究問題的結果。因為該二次函數(shù)的最小值為-2，所以-2為中心，各自去取值計算，結算結果如圖一，把計算的x，y的結果計算出來以后，先在坐標軸上進行繪圖，如圖二。通過對圖像的分析，得知該二次函數(shù)是軸對稱圖像，對稱軸是關于x=4的軸對稱，對稱軸經過坐標軸（-4，-2）。

2.3教學總結

通過創(chuàng)新教學的方式，在課堂教學中以學生為學習的主體，教師在發(fā)揮引導的作用，學生能充分能理解二次函數(shù)的性質和意義，增強學生學習的能力。以二次函數(shù)教學作為教學案例，體現(xiàn)了現(xiàn)在教學中，注重教學中的問題，傾向學生主動解決問題，學生在學習二次函數(shù)時應該注意做題的圖像和性質，要充分利用圖像進行解決問題。

3.結束語

利用二次函數(shù)作為教學案例，分析創(chuàng)新教學模式在初中數(shù)學中的運用，在教學中要遵循一定的教學原則，堅持學生作學習的主體，充分發(fā)揮教師的引導作用，教師在講課時要按照從易到難的原則和從具體到抽象的原則。初中數(shù)學中的二次函數(shù)本身具有一定的抽象性，教師運用創(chuàng)新的教學方法，把二次函數(shù)的內容更加形象化，學生在做題時應該充分利用圖像來學習。在新課程標準下，對初中數(shù)學進行教學改革，改變傳統(tǒng)的教學方式，運用創(chuàng)新的教學方式，提高學生自主探究學習的能力。

參考文獻：

[1]沈定祥.論新課程標準下初中數(shù)學教學模式的創(chuàng)新——以“二次函數(shù)”為例[J]. 新課程學習（下），2014，06：52-53.