輪腿式機器人的姿態耦合優化控制

徐　巖　段星光

1.河北師范大學，石家莊，050024　2.北京理工大學，北京，100081

輪腿式機器人的姿態耦合優化控制

徐巖1段星光2

1.河北師范大學，石家莊，0500242.北京理工大學，北京，100081

摘要：輪腿式移動機器人在不平坦地形下運動時涉及三個相互關聯的控制問題：穩定性控制、驅動牽引力控制和姿態控制。建立了適合于描述輪腿式機器人姿態的運動學模型，提出了輪腿運動模式下的穩定性函數和驅動牽引控制函數，為使機器人具有良好的地形適應能力、越障性能及運動穩定性，在綜合分析機器人穩定性和驅動牽引特性的基礎上，提出并構建了結合穩定性和驅動牽引性能的輪腿式機器人耦合優化控制準則，并實現了機器人姿態的優化控制，最后通過實驗驗證了該方法的可行性。

關鍵詞：輪腿式機器人；穩定性；驅動牽引特性；耦合優化

0引言

輪腿式機器人綜合了輪式機構運動效率高、速度快、便于控制與腿式機構環境適應性強、越障能力強、可以實現主動的姿態控制等優點，成為移動機器人中重要的一種類型,應用非常廣泛[1-6]。輪腿式機器人的典型特點是在腿式運動模式下,由于腿或輪子具有獨立驅動的自由度，所以姿態耦合優化后可使得這類系統具有控制自身姿態的能力[7-9]。對機器人運動姿態的控制會直接影響到機器人能否順利到達指定位置完成作業任務，建立考慮機器人穩定性、驅動牽引特性在內的機器人姿態耦合優化控制方法，實現機器人姿態的耦合優化控制，使其在運動過程中盡量保持車體始終處于水平穩定的姿態并具有良好的穩定性和驅動牽引特性，對穩定機器人視覺系統或作業系統，有效完成作業任務十分有益。

1優化控制問題描述

對輪腿式機器人的姿態優化控制的主要目的在于當其以腿式模式運動時，能夠實現運動穩定性、驅動牽引特性、穩定姿態等的耦合優化。要想實現其具有自主性質的運動功能，需要在確定各自優化控制標準的基礎上綜合考慮其耦合優化的控制方法。具體包含以下幾個方面。

(1)從輪腿式機器人的運動學模型來說,描述其姿態不再是簡單的姿態向量,還包含了機器人車體在空間的俯仰角、橫滾角、偏轉角，另外還包含了車體相對于運行地面的位置，以及兩側擺臂相對于車體的方位和擺臂之間的距離等信息。

(2)機器人的穩定性是確保整個系統運動安全的首要前提，在腿式模式下，其穩定性控制為一個重要的問題。主要原因在于當機器人運行在不平坦的自然環境中時，未知多變的環境特點將不可避免地導致在運動中出現機器人的接觸力發生跳變，并很容易導致機器人失穩的情況發生。

(3)輪腿運動模式下的冗余驅動系統雖然提供了靈活的運動性能，但也由此而產生了機器人與環境的復雜交互所帶來的驅動力控制問題，如復雜的輪-地交互特性[10-11]。由此造成了機器人在運動過程中由于打滑、側滑等情況的出現而引起的驅動牽引力問題，優化機器人驅動牽引控制的目的就是通過建立驅動牽引優化約束使機器人具有理想的運動性能。

(4)實現機器人耦合優化的目的是以機器人能夠具有較高的運動能力和機動性并確保整個系統運動中的安全性為目標，通過對機器人運動控制中的姿態、穩定性、驅動牽引特性等的分析研究，建立機器人姿態耦合優化準則和控制策略，使機器人的總體自主性能可以通過最大程度地提高機構的運動特性來實現，在一定程度上彌補系統智能的不足。

(5)通過確定運動學姿態描述，利用必要的傳感信息來獲取機器人當前姿態，通過建立合理的優化姿態向量和優化目標函數，尋求優化的姿態控制向量，實現基于機器人姿態控制的少傳感信息反饋的姿態優化運動控制。過于復雜的信息獲取手段勢必造成機器人系統的復雜性、信息處理的復雜性，甚至影響到機器人的總體性能指標。

2輪腿模式運動學分析與建模

2.1輪腿運動模式下機器人姿態

機器人在輪腿式運動模式下的機構簡圖見圖1。

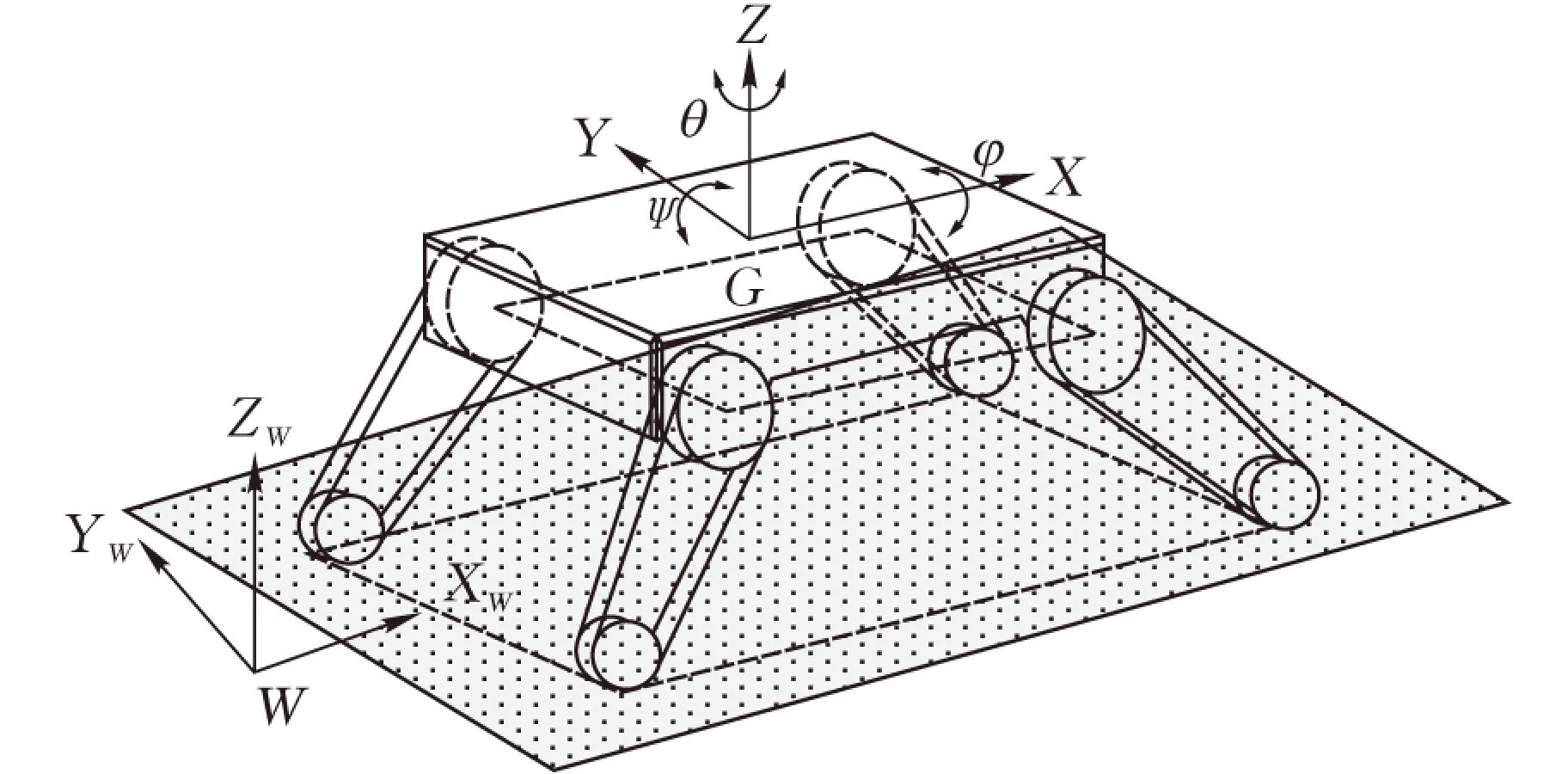
圖1　坐標系建立與姿態描述

描述機器人姿態可以采用方向余弦法、角度給定法等，本文采取歐拉角方位表示法。定義三個角度：繞X軸旋轉的為橫滾角φ；繞水平軸Y旋轉的為俯仰角Ψ；繞鉛垂軸Z旋轉的為偏轉角θ。用MRPY表示橫滾、俯仰和偏轉三個旋轉的組合所構成的旋轉矩陣來表示機器人車體的姿態,即

MRPY(φ,Ψ,θ)=R(z,θ)R(y,Ψ)R(x,φ)=

(1)

其中，cθ、cφ、cΨ為cosθ、cosφ、cosΨ的簡寫形式，sθ、sφ、sΨ為sinθ、sinφ、sinΨ的簡寫形式。

2.2輪-地接觸點與腿部控制參數

定義αi(i=1,2,3,4)為腿部的關節角變量,代表從擺臂旋轉中心沿擺臂長度方向與車體坐標系的X軸正向的夾角,并且逆時針方向為正。建立輪-地接觸模型如圖2所示。于是，每一個輪-地接觸點Pi的位置(xi,yi,zi)可以表示為

(2)

式中,LX為機器人前后輪之間的軸距；αi為關節角；LA為機器人履帶腿長度；w為兩側履帶間的距離；r為小履帶輪的半徑。

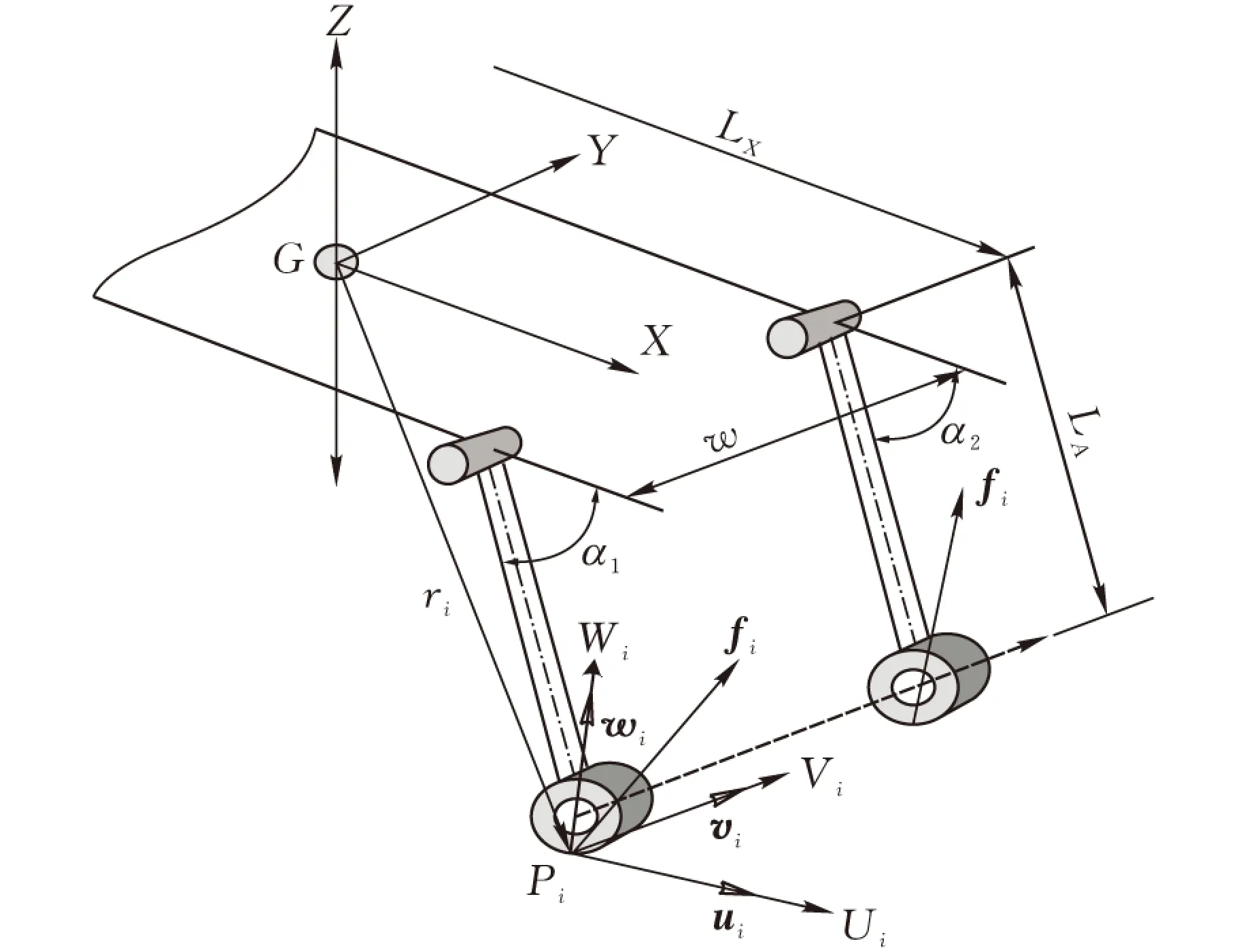
圖2　輪-地接觸模型

對于特定的機器人機構來說,參數LX、w、LA、r為常量,αi為控制變量。機器人姿態由每條腿的位置決定,可通過一套關節角參數(α1,α2,α3,α4)來確定(圖3)。

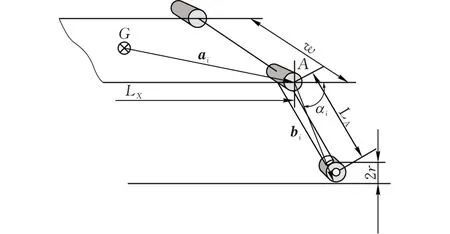
圖3　機器人腿部控制參數

定義ai是用來確定關節點A位置的向量,用來確定每條腿的位置，方向從重心G指向點A，定義向量bi從A點指向輪-地接觸點Pi,對特定的機器人結構,A點的位置是固定的，即ai是一個常向量,與Pi一起位于平臺坐標系XGZ的矢狀平面內。因此有

ai=(xi,yi,zi)T

bi=(Xi,0,Zi)T

對于已經設計好的機器人來說,每條履帶腿關節位置是固定的,在平臺坐標系的XGZ的矢狀平面內有

(3)

于是：

bi=(Xi,0,Zi)T=

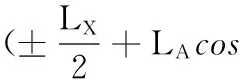
即,位置矢量bi是以關節角αi為自變量的函數。

3傾斜邊界穩定性準則

在腿式運動模式下,機器人運動的穩定性非常重要。針對腿式機器人的穩定性評價準則，許多學者提出了各種不同的穩定性評價標準[12],主要有：穩定性邊界[13]、傾角穩定邊界[14]、能量穩定性評價標準[15-16]等。通過綜合比較各種穩定性評價標準的特點，采用Papadopoulos等[14]提出的“傾斜邊界穩定性”標準更加適用于輪腿式機器人的穩定性評價。這個穩定性準則綜合了重心投影到支撐邊界的距離和由接觸點Pi所定義的平均平面的垂直方向的位置兩個要素，并且這種方法的計算是有效的。

如圖4所示，順次連接兩個連續地形之間接觸點Pi(i=1,2,3,4)構成各條傾覆軸線,連接重心G到傾覆軸線中點構成單位向量Ii,首先計算各單位向量Ii，然后計算由每一個Ii與作用到機器人上的合外力fr形成夾角θi作為各個傾覆軸的穩定角度,由各個θi給出相應于該傾覆軸的穩定角度。整個機器人車輛的穩定邊界φs定義為所有穩定角θi中的最小值,即

φs=minθi

(4)

當φs<0時，不穩定傾倒就會發生。

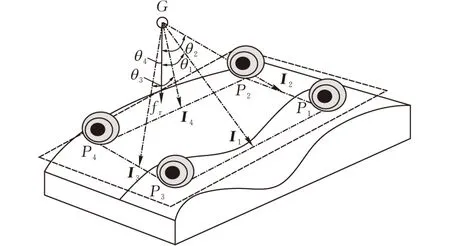
圖4　傾斜邊界穩定性

4驅動牽引力分析

4.1力的分布

在圖2中,Pi為各個輪-地接觸點，wi為Pi點處的局部法向量,fi為接觸力向量,G為系統的質心。依據螺旋理論及其虛功原理可以獲得系統的動力學方程為

Lf=W

其中,L為6×3n的位置關聯矩陣，n為接觸點個數；f為3n×1的接觸力向量；W為6×1的負載旋量。

驅動力的控制問題實際上就是針對W的接觸力fi的分布計算問題。因為方程Lf=W的位置關聯矩陣L可以通過改變機器人的姿態形狀來變化,所以,改善牽引特性和穩定性可以通過改變機器人姿態和形狀并應用力分布中的冗余特性來實現優化。類似的優化問題也存在于多指抓取的系統中。

4.2局部接觸力

在建立了輪地接觸點Pi處的局部坐標系Ri=(Pi,Ui,Vi,Wi)的基礎上,把接觸點處的接觸力向量fi沿三個局部坐標系的坐標軸分解為fi=(fu i,fv i,fw i)。其中,fw i為垂直于接觸平面切線方向的法向分量；fu i為第i個車輪的切向力分量；fv i為沿第i個輪軸方向的分量。

從驅動牽引力的角度看,切向分力fu i和法向分力fw i的大小直接影響其牽引特性。為此定義滑行率Si為切向合力與法向力之比來評價其牽引驅動特性,表示為

(5)

牽引效率主要與每個輪地接觸點的打滑特性有關，減小機器人打滑等價于使每一個Si取得最小值，于是，對于每個輪地接觸點Pi，提高其牽引特性就是使Si最小，對整個機器人而言，為提高牽引力就是要使所有Si中的最大值取得極小。于是得優化函數為

設輪地接觸時的摩擦因數為μf,則在Si≥μf時就可以滿足其能控性極限條件。

從接觸力的角度來看機器人運動穩定性,可以直觀地得到：為了使機器人保持穩定運動，必須保證所有法向分量為正，因為負的法向分量意味著機器人在該輪地接觸點沒有被地面支撐,即：fw i>0。

對于以上問題存在兩個方面的限制。一是機器人通過相關信息的獲取進行的主動姿態控制實際上所實現的是重心的變化,而這個變化的響應速度應該足夠快以便適應地形條件，否則不能完成實時的姿態調整控制。但是,由于機器人的運動速度在該種運動模式和地形條件下一般是很低的，所以這個限制不是一個嚴重的問題。第二個限制來自于復雜運動鏈的位置運動學分析，由于閉鏈位置運動學的復雜性以及源于力分布的冗余而帶來的優化問題，不適合于實時求解，所以實現機器人優化控制采用了“準平面”地形的概念以及實時次優化的方法。

4.3接觸力的平衡

機器人接觸力的平衡問題是機器人運動中影響牽引和穩定性能的重要因素，為此，我們建立機器人各個輪地接觸力平衡的標準如下。

接觸力平衡分布指標：

(6)

其中,0≤Bf≤1，fw i為第i個擺臂的垂直于接觸平面切線方向的合力，G為機器人重量。

當力平衡達到最優時,Bf可取得最大值。當Bf=0時,表明至少有一個輪子沒有與地面接觸，是一種極易產生不穩定的狀態。

5耦合優化控制

5.1耦合優化函數

機器人姿態在很大程度上取決于地形情況，耦合優化的目的是使車體盡量保持水平狀態，并且實現穩定性與牽引力的優化控制。而能實現姿態優化控制的地形只有在一定的范圍內才是可行的，也就是說，我們不能期望在任何地形幾何特性劇烈變化的情況下都可以實現，其控制效果受到機器人本身結構大小及其機構運動特點的限制。為研究出可行的控制算法，有必要對機器人的運動地形作適當的限制或者簡化。

由于在機器人運動的過程中，幾乎不能夠通過傳感檢測的方式得到輪地接觸點Pi所在地形的切平面，因此可以假定在輪地接觸點的局部小范圍內接觸表面是一個水平面，也就是說，用四個離散的、不連續的、具有不同高度的局部水平面來表示各個瞬時狀態的地面情況，并假定機器人的每條腿均與地面接觸。

對姿態優化控制可以表述為:對于特定的機器人系統,給定一套姿態控制參數P,通過適當地優化以便尋找優化姿態向量P*，使得目標函數Φ(P)最小。

這個目標函數綜合了對牽引力和穩定性的優化，是一個表征機器人運動性能標準的函數。結合穩定性準則和牽引力優化準則，取二者的加權均方根之和作為耦合優化標準函數：

(7)

其中，Si為滑行率，它是fi的函數；θi為穩定性傾角；Ks和Kf為加權系數，是常量。

控制目標是使得該函數最小化，即使得Φ(P)最小，而這個函數的最小化必然導致θi的最大化和Si的最小化，θi的最大化就是最大化機器人的穩定性，Si的最小化也就是減小整個機器人的滑行運動。

由于應用該目標函數需要局部的地圖信息以便定義接觸點Pi和相應的法向量wi,而一般情況下地形是未知的,Pi和wi不得不在線獲得。因此，這種方法的主要缺點是接觸法向量的測量以及在線優化過程的計算消耗。所以，需要在機器人的姿態控制中進行適當簡化，并采用次優化的方法來實現姿態控制。

5.2耦合優化控制與實現

耦合優化控制過程中，如果φs<0,則需要首先進行穩定性調節,否則可以進行組動力控制。其控制流程如圖5所示。

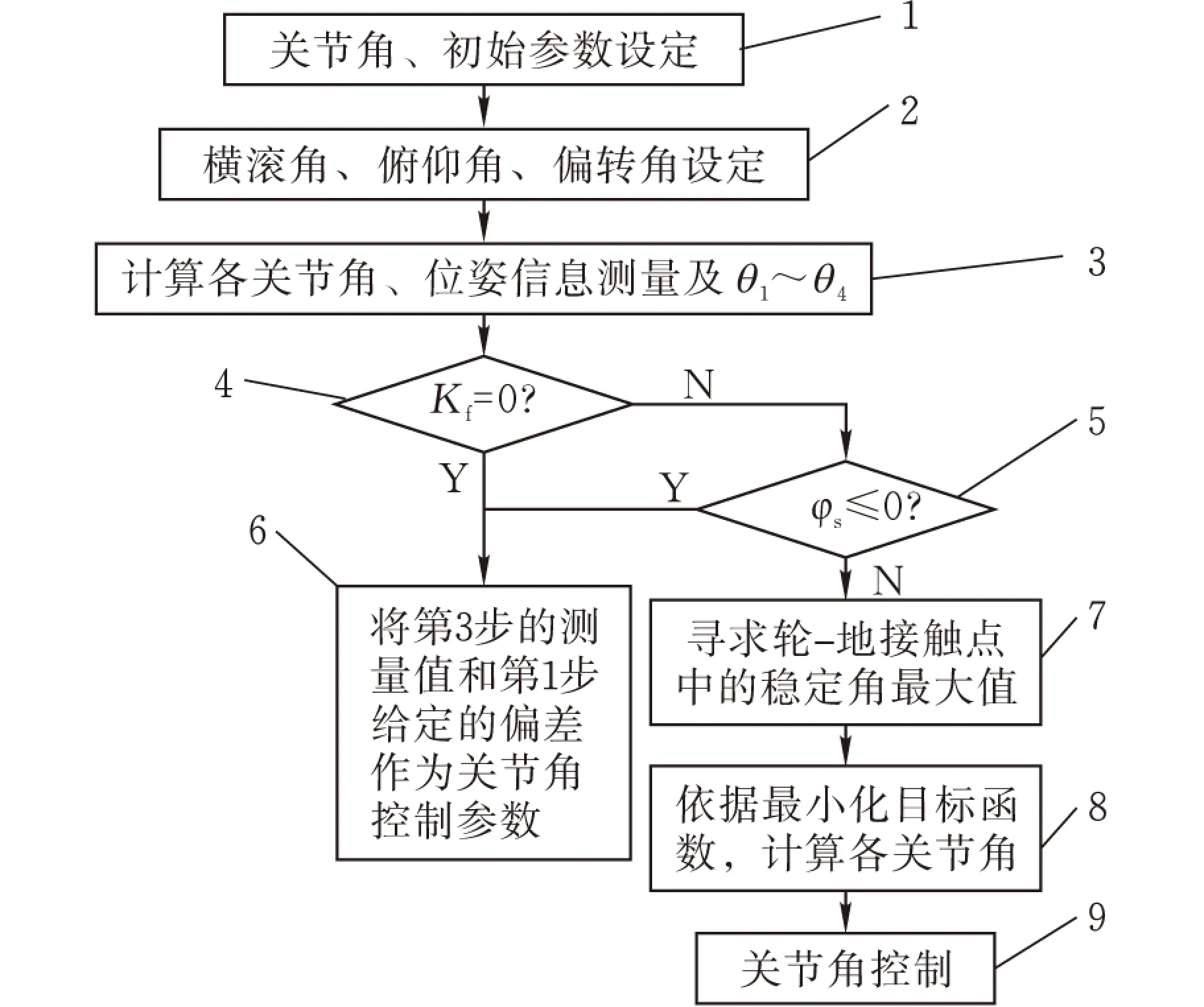
圖5控制流程圖

系統控制由四部分構成：感知系統、機器人本體、決策單元和執行單元，如圖6所示。機器人本體的初始姿態以及俯仰角、偏轉角和橫滾角及其重力信息通過機器人模型和感知系統獲得，經傳輸轉換到決策單元并經由決策單元傳輸到控制電機執行。利用感知信息和決策系統分別計算得到θ

1

、θ

2

、θ

3

、θ

4

。當K

f

=0或K

f

≠0且φ

s

≤0時進行穩定性控制,并使得φ

s

=

min

θ

i

(i=1,2,…,n);當K

f

≠0并且φ

s

>0時執行驅動牽引力控制。

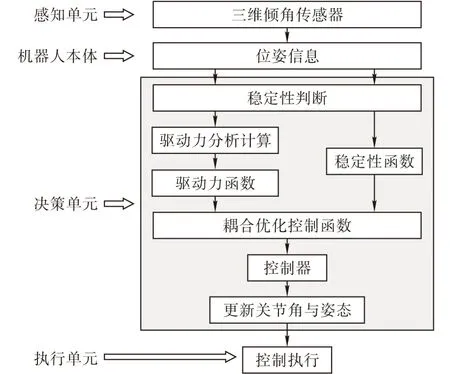
圖6　控制結構框圖

6實驗

實驗采用機器人在一定傾斜角度的水泥路面上運動來驗證姿態控制的有效性。所采用的地形如圖7所示。其斜面的傾斜角βs=12°,設機器人前進方向的偏航角為θ(為機器人前進方向的X軸和斜面最大斜度線之間的夾角)。為了對姿態控制效果進行比較說明，選擇一個在運動過程中始終保持不變的固定姿態為：在水平面上，機器人的所有擺臂均與地面垂直(即αi=±90°),稱這一姿態為固定姿態。

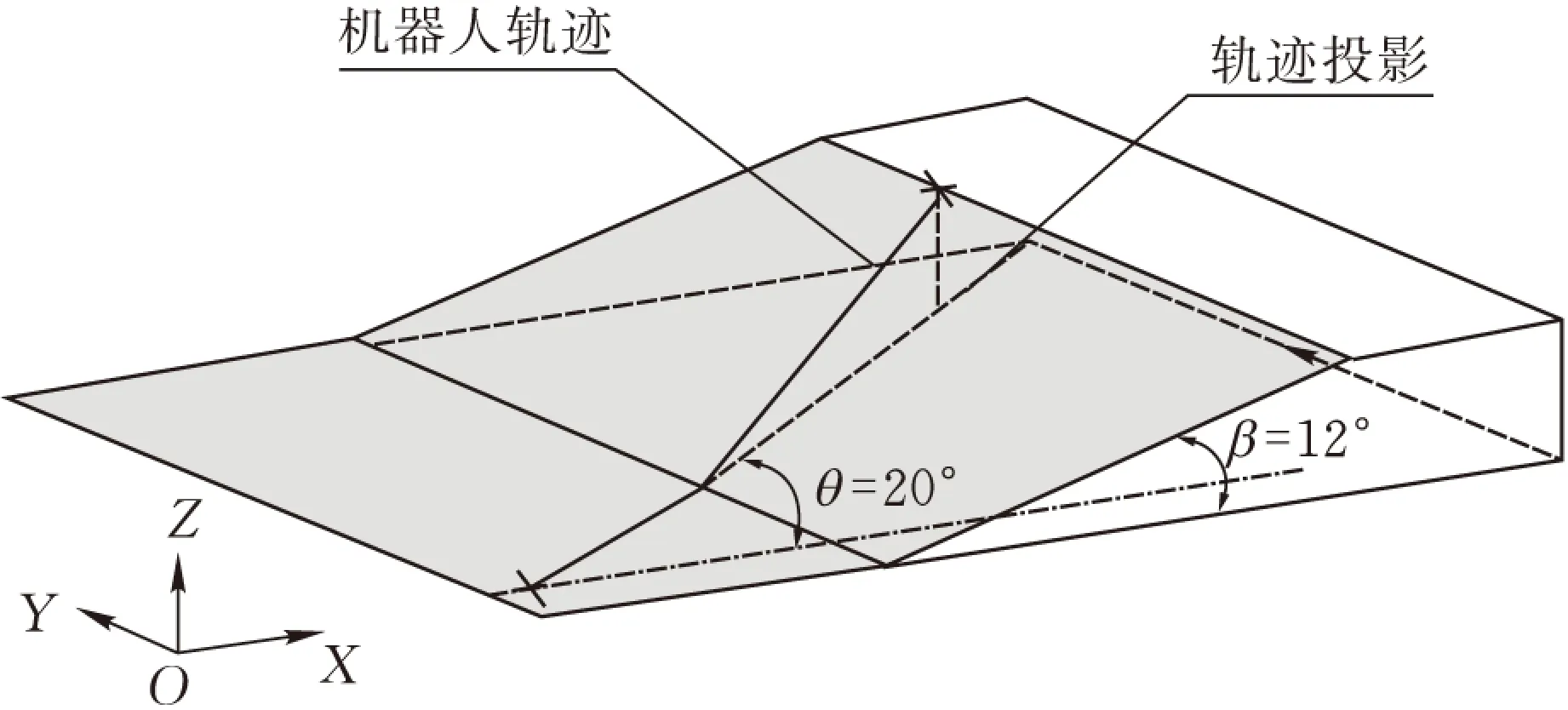
圖7　機器人姿態控制實驗環境

(1)設定偏航角θ=0°,使機器人采用固定姿態沿著最大斜度的方向以20cm/s的速度移動。此時,由于不采用姿態控制方法,機器人的橫滾角、俯仰角完全依賴于地形的變化,其橫滾角始終為0°,而俯仰角(此處即為斜面傾角β)變化如圖8所示。在圖8中，虛線表示了地形輪廓變化,實線代表了機器人采用姿態控制時其橫滾角和俯仰角的變化情況，從圖中可以看出，由于采用了姿態控制，使得機器人的俯仰角減小并使機器人車體盡量保持水平狀態,并且由于姿態優化控制使得θi增大，進一步提高了機器人運動的穩定性。

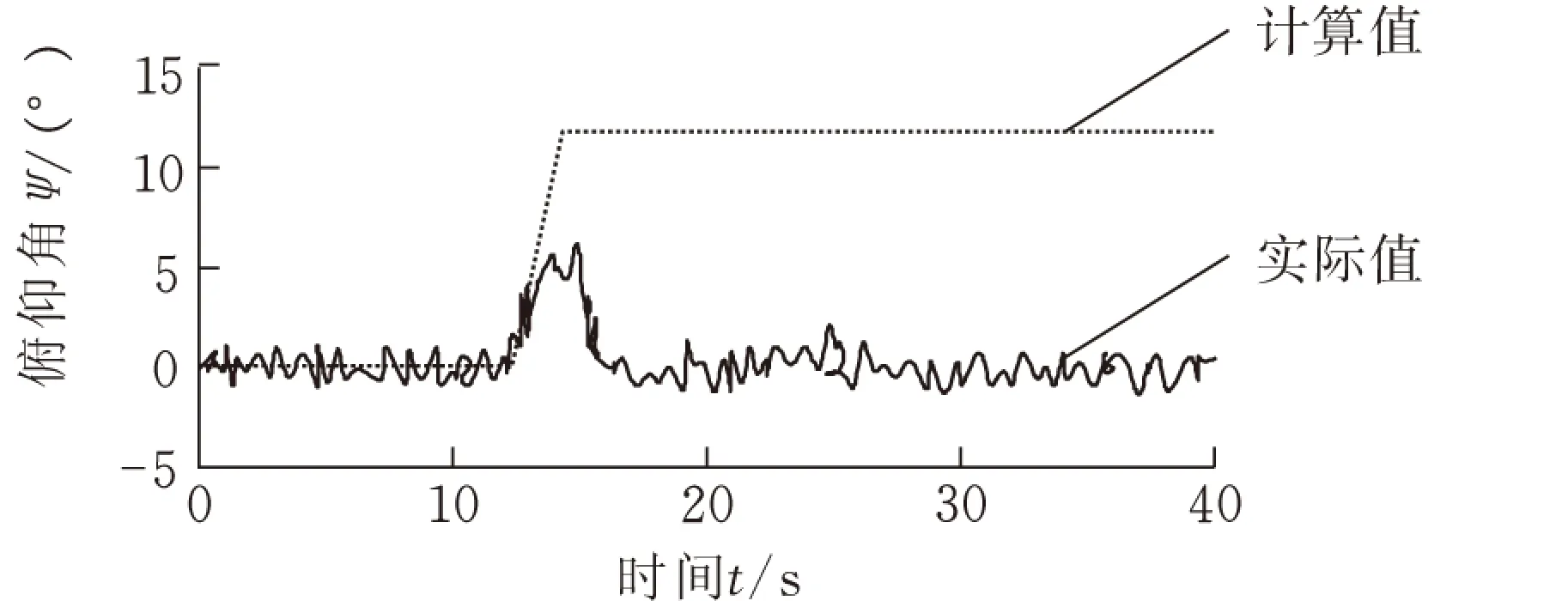
(a)俯仰角

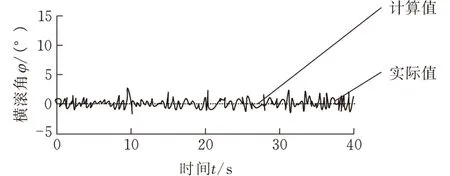
(b)橫滾角圖8　θ=0°時斜面上的姿態控制

(2)設定偏航角θ=20°，使機器人以20cm/s的速度移動。此時，在運動過程中俯仰角Ψ和橫滾角φ都需要控制。姿態控制的理想姿態是俯仰角和橫滾角均為0°并保持一個不變的地面高度Hg。

在圖9中，虛線表示了地面斜坡在俯仰和橫滾兩個方向的理論角度變化情況，依據如下公式計算得到其橫滾角和俯仰角：

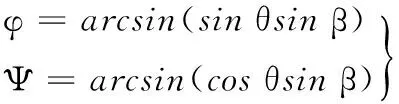
(8)

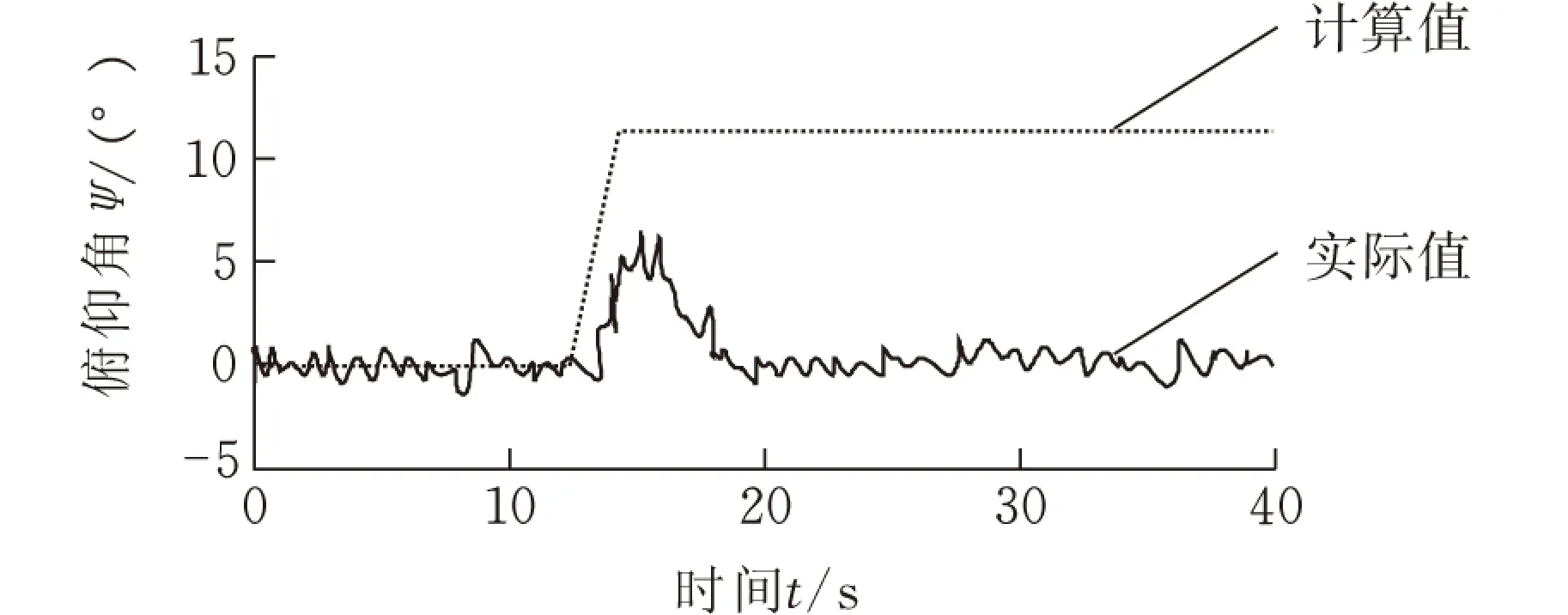
(a)俯仰角

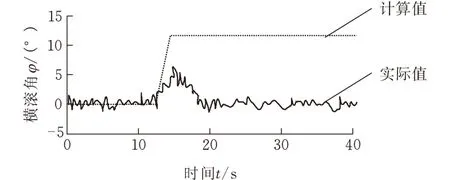
(b)橫滾角圖9　θ=20°時斜面上的姿態控制

圖9中的實線代表了當采用了姿態控制時機器人的俯仰角和橫滾角。從圖9中可以看出，當采用姿態控制后，機器人俯仰角和橫滾角得到明顯減小。在每一個斜坡最高點出現尖峰誤差是受機器人腿部反饋控制的響應速度的影響所致。另外,由于姿態優化控制使得θi增大，提高了機器人運動的穩定性，但在驅動牽引特性方面，Si會適當增加，由于耦合優化控制函數Φ(P)既考慮到穩定性又考慮到驅動牽引特性，所以在采取耦合優化控制后，兼顧了兩個方面的要求，并保證機器人車體盡量保持水平狀態，這對于機器人穩定視覺與機器人作業具有重要的意義。

7結語

本文針對輪腿式機器人的姿態控制問題提出了一種機器人姿態耦合優化控制方法，在機器人運動學模型及姿態表達模型的基礎上，建立了機器人穩定性控制與驅動牽引力控制準則，并結合輪腿式機器人的姿態控制特點，構建了耦合優化控制準則，實現了機器人姿態的優化控制，并通過實驗進行了可行性驗證。通過機器人的耦合優化控制，可以使機器人在運動過程中盡量保持車體處于水平穩定的姿態,這對穩定機器視覺系統、作業系統有著十分重要的意義，使得機器人的自主運動不過多地依賴于對環境的建模和大量信息處理，在一定程度上彌補了系統智能方面的不足。

參考文獻:

[1]GrandC,AmarBF,PlumetF,etal.DecoupledControlofPostureandTrajectoryoftheHybridWheel-leggedRobotHylos[C]//Proc.oftheIEEEInt.Conf.onRobotics&Automation.NewOrleans,LA,UnitedStates,2004:5111-5116.

[2]CholBJ,SreenivasanSV.MotionPlanningofaWheeledMobileRobotwithSlip-freeMotionCapabilityonaSmoothUnevenSurface[C]//Proc.oftheIEEEInternationalConferenceonRobotics&Automation.LeuvenBelgium,1998:3727-3732.

[3]MatthiesL,XiongY,HoggR,etal.APortable,Autonomous,UrbanReconnaissanceRobot[J].RoboticsandAutonomousSystems,2002,40:163-172.

[4]SreenivasanSV,WilcoxBH.StabilityandTractionControlofanActivelyActuatedMicro-rover[J].JournalofRoboticSystems,1994,11(6):487-502.

[5]DuanXingguang,HuangQiang,LiKejie.DesignandMotionAnalysisofMiniatureWheel-track-leggedMobileRobot[J].ChineseJournalofMechanicalEngineering,2005,41(8):108-114.

[6]DuanXingguang,HuangQiang,LiJingtao.DesignandImplementationofaSmallGroundMobileRobotwithMulti-locomotionModes[J].ChinaMechanicalEngineering,2007,12(1):8-12.

[7]GrandC,AmstMB,PlumetF,etal.StabilityandTractionOptimizationofaReconfigurableWheel-leggedRobot[J].TheInternationalJournalofRoboticsResearch,2004,23(10/11):1041-1058.

[8]GlockerM,vonStrykO.AHybridDynamicSystemsApproachtoOptimalDynamicRoleAssignmentandPhysics-basedRobotTrajectoryPlanningInRobocup[C]//RobocupInternationalSymposium.Osaka, 2005:18-19.

[9]AmarbfGC,PlumetF,etal.DecoupledControlofPostureandTrajectoryoftheHybridWheel-leggedRobotHylos[C]//Proc.oftheIEEEInt.Conf.onRobotics&Automation.NewOrleans,2004:5111-5116.

[10]ChoiBJ,SreenivasanSV.GrossMotionCharacteristicsofArticulatedMobileRobotswithPureRollingCapabilityonSmoothUnevenSurfaces[J].IEEETransactionsonRoboticsandAutomation,1999,15(2):340-343.

[11]SongZ,HutangkabodeeS,ZweiriYH,etal.IdentificationofSoilParametersforUnmannedGroundVehiclesTrack-terrainInteractionDynamics[C]//SICEAnnualConference.Sapporo,Japan.2004: 2255-2260.

[12]HiroseS,TsukagoshiH,YonedaK.NormalizedEnergyStabilityMarginandItsContourofWalkingVehiclesonRoughTerrain[C]//ProceedingsoftheIEEEInternationalConferenceonRobotics&Automation.Seoul,2001: 181-186.

[13]McgheeR,FrankA.OntheStabilityPropertiesofQuadrupedCreepingGait[J].MathematicalBioscience, 1968, 3: 331-351.

[14]PapadopoulosEG,ReyDA.ANewMesureofTipoverStabilityforMobileManipulators[C]//IEEEInt.Conf.onRoboticsandAutomation.Minneapolis,1996:3111-3116.

[15]MessuriDA,KleinCA.AutomaticBodyRegulationforMaintainingStabilityofaLeggedVehicleduringRoughTerrainLocomotion[J].IEEEJournalofRoboticsandAutomation,1985,Ra-1(3):132-141.

[16]GhasempoorA,SepehriN.AMeasureofMachineStabilityforMovingBaseManipulators[C]//IEEEInrernationalConferenceonRoboticsandAutomation.Nagoya,Japan,1995:2249-2254.

(編輯王艷麗)

Posture Coupled Optimization Control of Wheel-legged Robot

Xu Yan1Duan Xingguang2

1.Hebei Normal University,Shijiazhuang,0500242.Beijing Institute of Technology,Beijing,100081

Abstract：When wheel-legged mobile robots moved in uneven terrains,three basic non-isolated control problems such as stability control,drive traction control,and posture control were produced.Herein kinematic model with wheel-legged mode was established firstly, which was suitable to describe the robot posture. Then stability and traction functions were addressed.In order to have good adaptability,high maneuverability of negotiation and high locomotion security,coupled optimization function was built and coupled optimization control was realized based on the comprehensive analyses of the stability and traction characteristics,which could supply the coupled optimization criteria for stability and traction,and realize the posture optimization control of the robots. The effectiveness of the method was confirmed by experiments.

Key words:wheel-legged robot;stability;drive traction characteristics;coupled optimization

收稿日期：2015-04-28

基金項目:國家自然科學基金資助項目(61473111)

中圖分類號：TP24

DOI：10.3969/j.issn.1004-132X.2016.04.001

作者簡介：徐巖,女,1966年生。河北師范大學職業技術學院教授。研究方向為先進制造技術、機器人技術。段星光，男，1966年生。北京理工大學機電學院教授、博士研究生導師。