基于改進(jìn)小波神經(jīng)網(wǎng)絡(luò)的極譜法多金屬離子濃度檢測(cè)信號(hào)的在線解析

王雅琳，黃凱華，黃天紅，周曉君，陽(yáng)春華(中南大學(xué) 信息科學(xué)與工程學(xué)院，湖南 長(zhǎng)沙，410083)

?

基于改進(jìn)小波神經(jīng)網(wǎng)絡(luò)的極譜法多金屬離子濃度檢測(cè)信號(hào)的在線解析

王雅琳，黃凱華，黃天紅，周曉君，陽(yáng)春華
(中南大學(xué) 信息科學(xué)與工程學(xué)院，湖南 長(zhǎng)沙，410083)

摘要：針對(duì)極譜法實(shí)現(xiàn)鋅濕法冶煉過(guò)程多金屬離子濃度同時(shí)檢測(cè)時(shí)所得信號(hào)存在重疊峰的問(wèn)題，提出一種基于改進(jìn)小波神經(jīng)網(wǎng)絡(luò)的多金屬離子濃度極譜檢測(cè)信號(hào)在線解析方法。首先，采用離散小波變換求取極譜檢測(cè)信號(hào)的一階導(dǎo)數(shù)，從而提取出極譜信號(hào)的特征點(diǎn)作為小波神經(jīng)網(wǎng)絡(luò)的輸入；然后，提出一種改進(jìn)的狀態(tài)轉(zhuǎn)移算法優(yōu)化小波神經(jīng)網(wǎng)絡(luò)參數(shù)，實(shí)現(xiàn)基于小波神經(jīng)網(wǎng)絡(luò)的多金屬離子濃度同時(shí)測(cè)定信號(hào)的離線建模和在線解析，提高多金屬離子濃度同時(shí)測(cè)定的檢測(cè)精度。以實(shí)際鋅、鈷極譜重疊信號(hào)為例進(jìn)行驗(yàn)證。研究結(jié)果表明：所提出的方法針對(duì)鋅質(zhì)量濃度和鈷質(zhì)量濃度的測(cè)定結(jié)果優(yōu)于傳統(tǒng)的曲線擬合和基于BP神經(jīng)網(wǎng)絡(luò)的方法所得結(jié)果。

關(guān)鍵詞：極譜曲線；多金屬離子濃度；小波神經(jīng)網(wǎng)絡(luò)(WNN)；狀態(tài)轉(zhuǎn)移算法(STA)

在鋅濕法冶煉過(guò)程中，存在其他多種雜質(zhì)金屬離子，這些雜質(zhì)金屬離子通過(guò)凈化過(guò)程添加其他物料除去。除雜物料添加過(guò)多會(huì)造成資源浪費(fèi)；物料添加不足就會(huì)造成雜質(zhì)金屬離子去除不徹底，對(duì)后續(xù)電解工藝將存在很大的影響。長(zhǎng)期以來(lái)，在冶煉過(guò)程中多金屬離子濃度的檢測(cè)采用人工離線檢測(cè)的方法，這種檢測(cè)過(guò)程復(fù)雜且滯后時(shí)間長(zhǎng)，不能及時(shí)反饋濃度信息以優(yōu)化物料的添加量，造成資源浪費(fèi)、污染物排放超標(biāo)和能源過(guò)量消耗等嚴(yán)重后果，因此，亟需研究針對(duì)濕法冶金過(guò)程多金屬組分濃度的同時(shí)在線分析方法，以便及時(shí)優(yōu)化過(guò)程參數(shù)并實(shí)現(xiàn)節(jié)能減排降耗[1?2]。MAHER 等[3]在綜合分析凈化過(guò)程工藝流程和檢測(cè)參數(shù)特點(diǎn)的基礎(chǔ)上，引入極譜分析方法用于鋅濕法冶煉過(guò)程硫酸鋅溶液多金屬離子濃度的在線檢測(cè)，不需要進(jìn)行信號(hào)轉(zhuǎn)換，根據(jù)產(chǎn)生的伏安特性曲線就可計(jì)算出待檢離子的濃度，具有靈敏度高、速度快、操作方便等特點(diǎn)。但在極譜法檢測(cè)過(guò)程中，對(duì)于特性相似的組分，由于激發(fā)電壓接近會(huì)得到重疊信號(hào)；另外，多組分中的主體成分由于其濃度高，產(chǎn)生的信號(hào)過(guò)強(qiáng)易掩蓋其他信號(hào)，從而產(chǎn)生信號(hào)疊加。對(duì)于多組分離子濃度的同時(shí)檢測(cè)，傳統(tǒng)化學(xué)量測(cè)常采用繁瑣冗長(zhǎng)的化學(xué)分離、掩蔽和提高儀器分辨率等方法來(lái)獲得單一組分的相關(guān)信息。然而，在很多情況下，僅憑化學(xué)方法和提高儀器的分辨率對(duì)多組分體系進(jìn)行分辨往往非常困難。近年來(lái)，化學(xué)計(jì)量學(xué)的發(fā)展為解決各種化學(xué)重疊峰分辨問(wèn)題提供了新的途徑。可通過(guò)借助某些數(shù)學(xué)或統(tǒng)計(jì)學(xué)方法,把通過(guò)化學(xué)方法和儀器未能完全分離的譜峰加以分解,從而得到各子信號(hào)的相關(guān)信息。國(guó)內(nèi)外學(xué)者提出了很多用于重疊信號(hào)解析的方法，如Fourier 變換、 曲線擬合[4]、 因子分析[5]、 小波分析[6?8]、人工神經(jīng)網(wǎng)絡(luò)[9?10]等。小波神經(jīng)網(wǎng)絡(luò)是神經(jīng)網(wǎng)絡(luò)領(lǐng)域中目前比較活躍的一個(gè)研究方向，是在小波分析與神經(jīng)網(wǎng)絡(luò)發(fā)展的基礎(chǔ)上形成的一種新型前饋網(wǎng)絡(luò)模型，不僅具有小波變換的優(yōu)點(diǎn)，而且在時(shí)域頻域具有良好的局部特性，同時(shí)具有多層前饋神經(jīng)網(wǎng)絡(luò)對(duì)連續(xù)光滑的函數(shù)可以任意精度逼近的優(yōu)點(diǎn)，近年來(lái)已逐漸被用于光譜[11]、色譜等重疊信號(hào)的解析中[12?13]。本文作者將小波神經(jīng)網(wǎng)絡(luò)應(yīng)用于極譜重疊信號(hào)的解析過(guò)程，以實(shí)現(xiàn)多金屬離子濃度的同時(shí)測(cè)定。首先采用離散小波變換求取極譜信號(hào)的一階導(dǎo)數(shù)，以此提取出相應(yīng)特征點(diǎn)。然后，將極譜信號(hào)特征點(diǎn)作為小波神經(jīng)網(wǎng)絡(luò)的輸入，相應(yīng)的多種金屬離子濃度作為輸出，進(jìn)行小波神經(jīng)網(wǎng)絡(luò)的參數(shù)訓(xùn)練，從而建立極譜電流信號(hào)與金屬離子濃度之間的關(guān)系。在小波神經(jīng)網(wǎng)絡(luò)的參數(shù)訓(xùn)練中，常用的梯度下降訓(xùn)練法具有收斂速度慢、易陷入局部極值而且對(duì)初值要求較高的不足[14]。為克服上述不足，本文采用改進(jìn)的狀態(tài)轉(zhuǎn)移算法優(yōu)化小波神經(jīng)網(wǎng)絡(luò)參數(shù)。最后，采用實(shí)際的鋅、鈷極譜重疊信號(hào)進(jìn)行測(cè)試以驗(yàn)證所提方法的有效性。

1　基于狀態(tài)轉(zhuǎn)移算法的小波神經(jīng)網(wǎng)絡(luò)

1.1狀態(tài)轉(zhuǎn)移算法基本原理

狀態(tài)轉(zhuǎn)移算法(STA)[15?16]是一種新的智能優(yōu)化算法，是基于控制理論中的狀態(tài)空間轉(zhuǎn)移思想，將優(yōu)化問(wèn)題的結(jié)果當(dāng)成1個(gè)狀態(tài)，在搜索空間進(jìn)行隨機(jī)全局搜索。該算法具有結(jié)構(gòu)簡(jiǎn)單、并行性好的特點(diǎn)，在復(fù)雜函數(shù)的參數(shù)尋優(yōu)搜索中具有良好的性能。與遺傳算法類似，狀態(tài)轉(zhuǎn)移算法同樣采用隨機(jī)搜索和迭代方法進(jìn)行尋優(yōu)處理，其尋優(yōu)過(guò)程即為狀態(tài)轉(zhuǎn)移，更新當(dāng)下最優(yōu)解的過(guò)程即為狀態(tài)轉(zhuǎn)移過(guò)程。

STA 算法具體操作步驟見(jiàn)表1，它有以下幾個(gè)核心操作：旋轉(zhuǎn)(rotation transformation)、轉(zhuǎn)移(translation transformation)、擴(kuò)展(expansion transformation)、平移(axesion transformation)。

1)對(duì)于旋轉(zhuǎn)算子，有

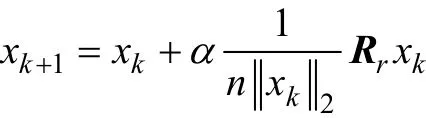
其中：xk∈Rn，代表1個(gè)狀態(tài)，對(duì)應(yīng)于優(yōu)化問(wèn)題的1個(gè)解決方案；α為旋轉(zhuǎn)因子，為1個(gè)正數(shù)；R∈Rn× n，r 為[?1,1]之間服從均勻分布的隨機(jī)矩陣。該算子使搜索算法在1個(gè)以 xk為中心、α為半徑的超球面內(nèi)進(jìn)行尋優(yōu)。

2)對(duì)于轉(zhuǎn)移算子，有

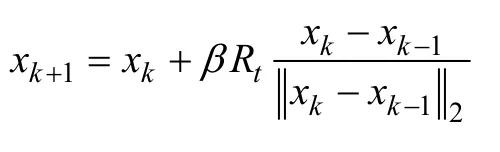
其中：β 為1個(gè)正數(shù)，稱為轉(zhuǎn)移因子；Rt∈R，為[0,1]之間的隨機(jī)數(shù)。該算子使算法沿著 xk? xk?1的正向梯度方向進(jìn)行搜索，搜索步長(zhǎng)最大為β。

表1　STA算法操作步驟Table1　Framework of STA

3)對(duì)于擴(kuò)展算子，有

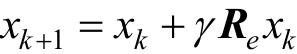
其中：γ為擴(kuò)展因子，為1個(gè)正數(shù)；R∈Rn× n，為服

e從高斯分布的對(duì)角矩陣(在文中采用的是服從標(biāo)準(zhǔn)正態(tài)分布)。擴(kuò)展算子能夠在整個(gè)搜索空間進(jìn)行擴(kuò)展 搜索。

4)對(duì)于平移算子，有

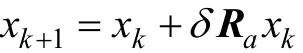
其中：δ 為1個(gè)正數(shù)，稱為平移因子；R∈Rn× n，為a服從高斯分布的對(duì)角矩陣，矩陣中只有1個(gè)隨機(jī)位置上的元素不為 0。平移算子能夠沿著某一變量的軸線進(jìn)行搜索，從而提高單維搜索力度。

狀態(tài)轉(zhuǎn)移算法(STA)的基本流程如表1所示。其中，Ibest為種群中的最優(yōu)個(gè)體，NSE為搜索種群的個(gè)體數(shù)，α，β，γ和δ 分別為旋轉(zhuǎn)因子、轉(zhuǎn)移因子、擴(kuò)展因子和平移因子。在表1的Step3中，只進(jìn)行擴(kuò)展、旋轉(zhuǎn)、平移3步操作，這是由于轉(zhuǎn)移算子已經(jīng)被嵌入到其他3步操作中。以擴(kuò)展操作為例詳細(xì)描述每種操作的搜索細(xì)節(jié)：

Ibest←擴(kuò)展(Ibest,NSE,β,γ)

1)Obest←Pbest，其適應(yīng)度為fbest。

2)將Obest復(fù)制成個(gè)體數(shù)為NSE的群體，進(jìn) 行擴(kuò)展操作后得到種群Pstate。計(jì)算Pstate中的個(gè)體適應(yīng)度，此時(shí)，群體最優(yōu)個(gè)體為Nbest，其適應(yīng)度為gbest。

3)若 gbest＜fbest(針對(duì)求極小值問(wèn)題)，則fbest←gbest，Gbest←Nbest，并執(zhí)行4)；否則執(zhí)行6)。

4)xk?1←Obest，xk←Gbest，各復(fù)制 NSE次，兩兩配對(duì)，分別按式(3)進(jìn)行轉(zhuǎn)移操作后得到種群Pstate。計(jì)算Pstate中的個(gè)體適應(yīng)度，此時(shí)的群體最優(yōu)個(gè)體為 Nbest，其適應(yīng)度為gbest。

5)若gbest＜fbest，則fbest←gbest，Gbest←Nbest。

6)將Gbest作為擴(kuò)展操作的輸出。

其中：Pbest為初始最優(yōu)值；Obest為操作前舊的最優(yōu)值；Nbest為操作后新的最優(yōu)值；Gbest為最終獲取的最優(yōu)值。

1.2狀態(tài)轉(zhuǎn)移算法改進(jìn)

1)旋轉(zhuǎn)算子在尋優(yōu)過(guò)程中，當(dāng) 所有變量的值都接近0時(shí)，該算子將陷入1個(gè)勢(shì)阱中。以二維決策變量x=[x1,x2]為例，取 x=[0,0]進(jìn)行旋轉(zhuǎn)算子的搜索k k仿真。令旋轉(zhuǎn)因子 α=1，進(jìn)行1×105次重復(fù)搜索，得到的 xk+1如圖1(a)所示(其中圓圈表示 xk，點(diǎn) 表示每次搜索得到的 xk+1)。從圖1(a)可以看出，所有的 xk+1都集中在原點(diǎn)，無(wú)法跳出。

為了解決這一問(wèn)題，本文提出改進(jìn)的旋轉(zhuǎn)算子：

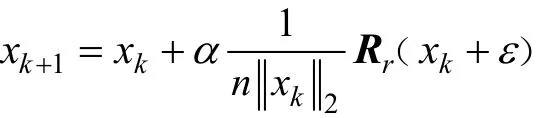
其中：ε 為1個(gè)較小值。經(jīng)實(shí)驗(yàn)驗(yàn)證，當(dāng)ε=0.01時(shí)，就能跳出勢(shì)阱，改進(jìn)后的旋轉(zhuǎn)算子搜索范圍如圖1(b)所示。

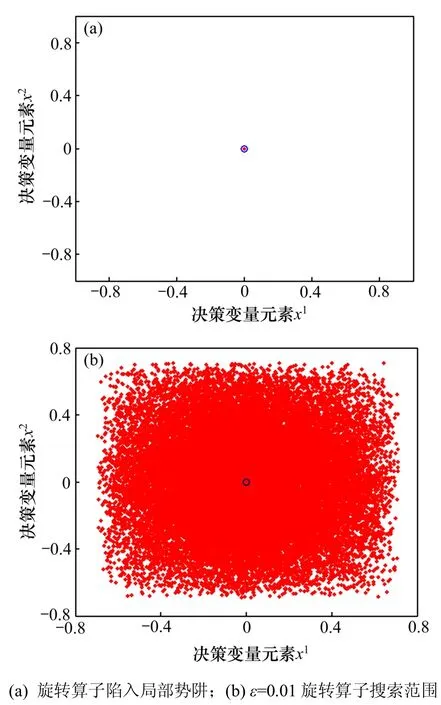
圖1　旋轉(zhuǎn)算子搜索范圍Fig.1　Search area of rotation transformation and improved rotation transformation

2)基本狀態(tài)轉(zhuǎn)移算法的轉(zhuǎn)移算子在搜索時(shí)是單向的，沿著 xk? xk?1的正向梯度方向進(jìn)行搜索。為了提高該算子的搜索能力，將 Rt∈R 的取值從[0,1]變?yōu)閇?1,1]，使其能夠沿著軸線雙向搜索。以二維決策變量為例，取 xk?1=[0,0]，xk=[1,1]進(jìn)行轉(zhuǎn)移算子的搜索仿真。令轉(zhuǎn)移參數(shù) β=1，進(jìn)行1×105次重復(fù)搜索，得到改進(jìn)前后的 xk+1如圖2所示(其中圓圈表示 xk，點(diǎn)表示每次搜索得到的 xk+1)。

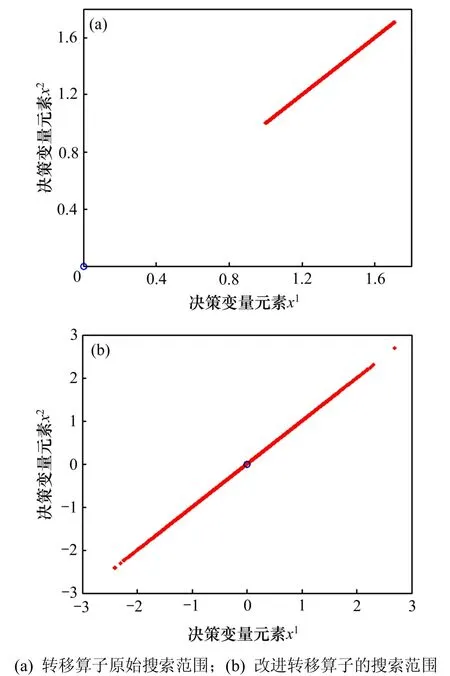
圖2轉(zhuǎn)移算子改進(jìn)前后的搜索范圍Fig.2Search area of translation transformation and improved translation transformation

圖3　小波神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)Fig.3　Structure of wavelet neural network

1.3改進(jìn)狀態(tài)轉(zhuǎn)移算法優(yōu)化的小波神經(jīng)網(wǎng)絡(luò) STAWNN

小波神經(jīng)網(wǎng)絡(luò)(WNN)是基于小波變換理論，用非線性小波基取代一般的神經(jīng)元非線性激勵(lì)函數(shù)而構(gòu)成的神經(jīng)網(wǎng)絡(luò)模型[17]。WNN網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)如圖3所示。該網(wǎng)絡(luò)含有p個(gè)輸入節(jié)點(diǎn)，q個(gè)隱層節(jié)點(diǎn)，n個(gè)輸出節(jié)點(diǎn)，采用單隱含層的神經(jīng)網(wǎng)絡(luò)，輸出層通常為線性神經(jīng)元，這里使用Morlet母小波，它將隱含層的小波伸縮系數(shù)進(jìn)行線性疊加形成輸出結(jié)果。WNN 的輸出表達(dá)式為

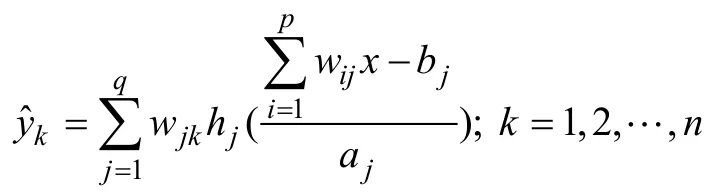
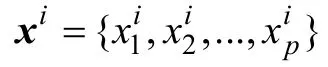
圖3所示的小波神經(jīng)網(wǎng)絡(luò)中需要訓(xùn)練的參數(shù)包括權(quán)重因子 wij和 wjk，小波基的伸縮因子 aj和平移因子 bj(i=1,2,…,p；j=1,2,…,q；k=1,2,…,n)。傳統(tǒng)方法利用梯度下降法對(duì)網(wǎng)絡(luò)進(jìn)行訓(xùn)練，由于對(duì)初始網(wǎng)絡(luò)參數(shù)的依賴性較大，算法容易陷入局部最優(yōu)，難以達(dá)到全局最優(yōu)，為了迅速找到全局最優(yōu)值，采用改進(jìn)的狀態(tài)轉(zhuǎn)移算法(STA)優(yōu)化小波神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)參數(shù)。S TA優(yōu)化小波神經(jīng)網(wǎng)絡(luò)(STA-WNN)的具體步驟見(jiàn)表2。

表2狀態(tài)轉(zhuǎn)移優(yōu)化小波神經(jīng)網(wǎng)絡(luò)具體步驟Table1　Framework of STA-WNN

2　基于STA-WNN的極譜法多金屬離子檢測(cè)信號(hào)在線解析方法

2.1極譜法離子濃度檢測(cè)基本原理

極譜法(polarography)是一類比較特殊的電解分析方法，通過(guò)激勵(lì)電位引起被分析溶液中的離子發(fā)生電解，繼而根據(jù)溶液中被測(cè)物質(zhì)在滴汞電極上進(jìn)行電解時(shí)所測(cè)得的電流?電壓曲線分析物質(zhì)含量[18?19]。以線性掃描極譜法為例，某種離子電解產(chǎn)生的電流?電壓曲線如圖4所示。圖4中：Ep和 Ip分別為極譜峰電位和峰電流；Ep/2和 Ip/2分別為極譜半波電墳和半波電流。由極譜學(xué)基礎(chǔ)原理可知：離子的質(zhì)量濃度ρ0與其極譜峰值電流 Ip成正比：ρ0∝ IP，因此，只需通過(guò)測(cè)量峰高即可得到離子質(zhì)量濃度。但當(dāng)同時(shí)測(cè)量幾種物質(zhì)時(shí)，若它們的半波電壓比較接近或存在某1個(gè)含量較高的主體成分時(shí)，其產(chǎn)生的電流?電壓曲線就會(huì)出現(xiàn)重疊，不能直接得到離子的峰高，這就為離子質(zhì)量濃度的定量分析帶來(lái)困難。以同時(shí)含有鋅、鈷離子的混合溶液為例，所得極譜曲線(除去了底液殘留曲線)如圖5所示。圖5中鈷離子曲線受到后面質(zhì)量濃度較大的鋅離子曲線的影響而產(chǎn)生鈷峰抬升且后移的假象，形成了1個(gè)較小的肩峰，這時(shí)鈷離子的質(zhì)量濃度將無(wú)法直接通過(guò)峰高得出，為此，需要采用合適的方法重新描述具有重疊峰特性的極譜信號(hào)與多個(gè)待測(cè)金屬質(zhì)量離子濃度之間的關(guān)系。這里采用 STA-WNN 來(lái)實(shí)現(xiàn)。

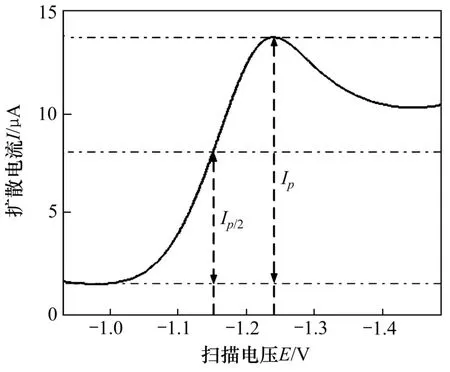
圖4線性掃描極譜法所得電流?電壓曲線Fig.4Current?potentialCurve using linear sweep polarograph

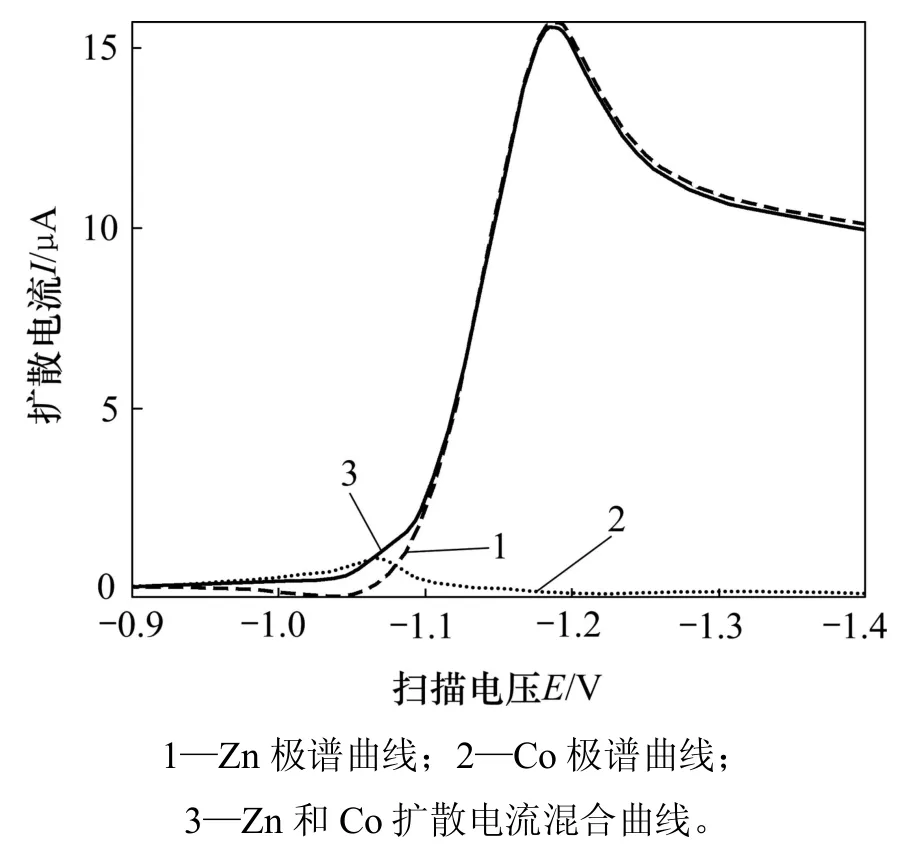
圖5　鋅、鈷線性極譜掃描電流?電壓曲線Fig.5　Current?potentialCurve of zinc andCobalt using linear sweep polarographic

離子質(zhì)量濃度與譜峰處的電流密切相關(guān)，因此，選取具有重疊峰極譜信號(hào)中峰值信息及其一階導(dǎo)數(shù)的相關(guān)信息作為特征點(diǎn)。在極譜曲線中，一般檢測(cè) n 個(gè)金屬離子的質(zhì)量濃度，就會(huì)出現(xiàn) n 個(gè)峰值點(diǎn)，其相應(yīng)的一階導(dǎo)數(shù)曲線就會(huì)有2n條。這些特征點(diǎn)在一定程度上反映了金屬離子的濃度，為此，將這3n個(gè)特征點(diǎn)作為小波神經(jīng)網(wǎng)絡(luò)的輸入。

以同時(shí)含有鋅、鈷離子的混合溶液所得的極譜曲線為例，首先選取極譜曲線中的2個(gè)峰值極大點(diǎn)(如圖6 中 A 和 B 點(diǎn)所示)作為特征點(diǎn)。然后，求取極譜掃描曲線的一階導(dǎo)數(shù)曲線。

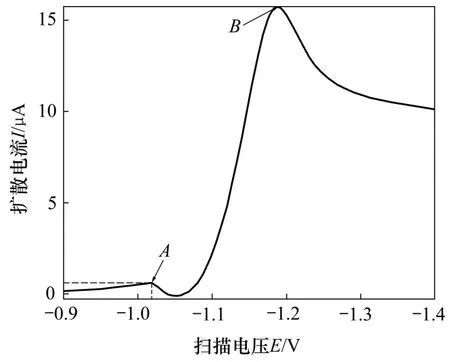
圖6　鋅和鈷線性極譜掃描電流?電壓曲線中特征值的提取Fig.6　Feature extraction values fromCurrent?potentialCurve of zinc andCobalt using linear sweep polarographic

在求取一階導(dǎo)數(shù)過(guò)程中，普通的導(dǎo)數(shù)法隨著求導(dǎo)階次的提高存在噪聲被放大的缺點(diǎn)，將小波變換應(yīng)用于信號(hào)求導(dǎo)能夠很好地克服這一不足。為此，采用離散小波變換求取信號(hào)的一階導(dǎo)數(shù)。離散小波變換[20?21]用于信號(hào)求導(dǎo)的原理如下。

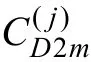
采用離散小波變換對(duì)圖 6中鋅、鈷離子的線性極譜掃描電流?電壓曲線進(jìn)行求導(dǎo)所得一階導(dǎo)數(shù)曲線，如圖7所示。

按照上述的特征值選取方法，選取鋅、鈷線性極譜掃描曲線(圖6)中的2個(gè)峰值點(diǎn)A和B，及其一階導(dǎo)數(shù)曲線(圖7)中的4個(gè)極值點(diǎn)C，D，E和F共6個(gè)特征點(diǎn)作為小波神經(jīng)網(wǎng)絡(luò)的輸入，用于基于 STA-WNN的多金屬離子濃度同時(shí)測(cè)定信號(hào)的離線建模和在線解析。

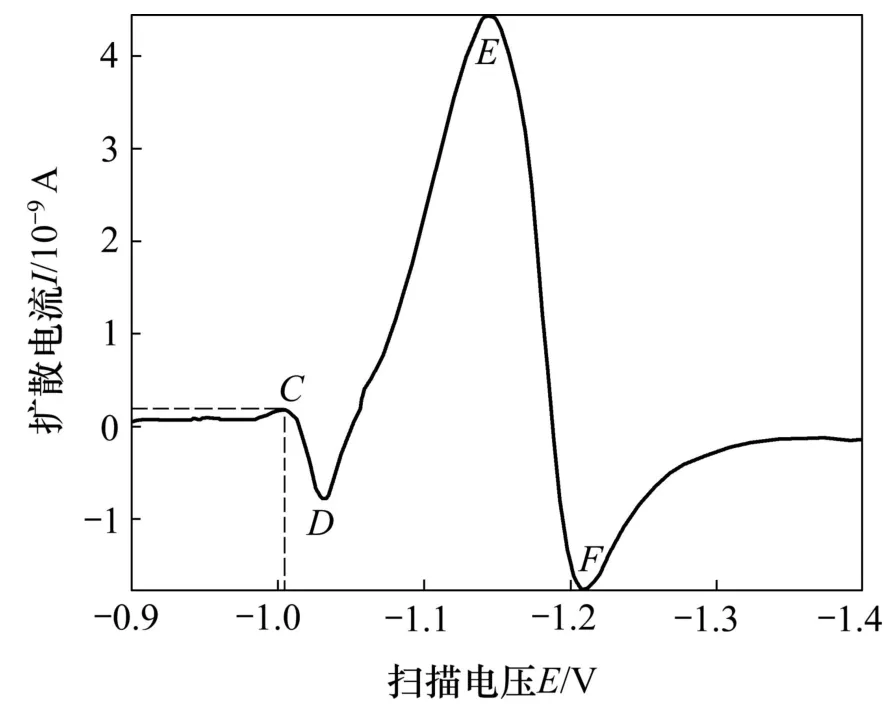
圖7　鋅、鈷線性極譜掃描電流?電壓曲線的一階導(dǎo)數(shù)中特征值的提取Fig.7　Feature extraction values for the first derivative of zinc andCobalt using linear sweep polarographic

2.2STA-WNN用于多金屬離子檢測(cè)信號(hào)在線解析的實(shí)驗(yàn)驗(yàn)證

將 STA-WNN 用于極譜法多組分離子檢測(cè)信號(hào)在線解析過(guò)程的主要思路為：首先采用正交設(shè)計(jì)方法配置多組多金屬離子混合溶液，并對(duì)每組溶液進(jìn)行線性極譜掃描；選取極譜掃描信號(hào)的峰值點(diǎn)以及極譜信號(hào)一階導(dǎo)數(shù)曲線的極值點(diǎn)組成特征點(diǎn)作為 WNN 的輸入，并以多金屬離子質(zhì)量濃度為 WNN 輸出，基于多組極譜法成分分析檢測(cè)樣本，采用所改進(jìn)STA方法離線訓(xùn)練 WNN，以獲得極譜信號(hào)與相應(yīng)的各離子濃度間關(guān)系的數(shù)學(xué)模型；最后，將訓(xùn)練好的 WNN 作為多金屬離子濃度同時(shí)測(cè)定信號(hào)的在線解析模型。

為驗(yàn)證所提方法的可行性和有效性，以鋅濕法冶金過(guò)程凈化后液中鋅、鈷離子濃度為對(duì)象，采用成都儀器廠的JP-06A型精密極譜分析儀進(jìn)行實(shí)驗(yàn)。實(shí)驗(yàn)按正交設(shè)計(jì)方法配制了14組包含不同質(zhì)量濃度的鋅、 鈷離子混合溶液(其中鋅離子質(zhì)量濃度范圍為 0.17～0.85 g/L，鈷離子質(zhì)量濃度范圍為0.002～0.20 mg/L)。并確定金屬離子質(zhì)量濃度成分檢測(cè)的環(huán)境：溶液溫度為20 ℃，p H=8.26。極譜分析儀對(duì)每組溶液在?0.9～?1.4 V的電壓范圍內(nèi)分別進(jìn)行線性掃描，每 0.1mV 記錄 3個(gè)數(shù)據(jù)點(diǎn)。將這些電流繪制在平面上，可得到類似圖6所示的極譜曲線。對(duì)于按梯度配置的14組混合溶液，采用極譜分析儀檢測(cè)得14組電流系列(即極譜曲線)，選其中9組(見(jiàn)表3)用于小波神經(jīng)網(wǎng)絡(luò)訓(xùn)練，以確定最優(yōu)的小波神經(jīng)網(wǎng)絡(luò)參數(shù)；剩余5組(見(jiàn)表4)作為測(cè)試數(shù)據(jù)驗(yàn)證多金屬離子檢測(cè)信號(hào)在線解析模型。

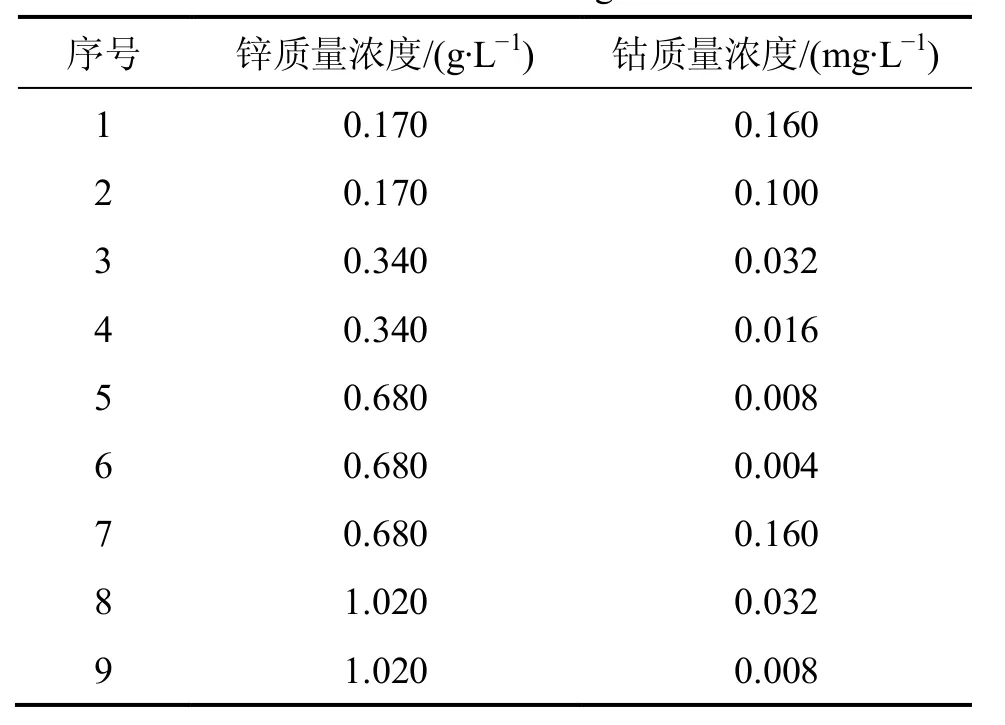
表3　訓(xùn)練集Table1　Training set

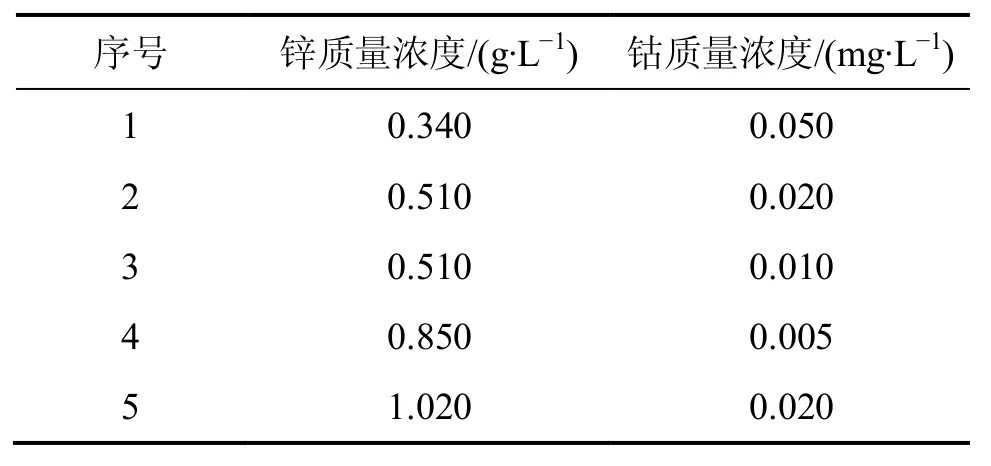
表4測(cè)試集Table1　Test set

由于每組極譜信號(hào)含有 2萬(wàn)多個(gè)電流，為此，按前面所述的方法確定極譜信號(hào)的6個(gè)特征值作為網(wǎng)絡(luò)輸入；并采用改進(jìn)狀態(tài)轉(zhuǎn)移算法優(yōu)化的小波神經(jīng)網(wǎng)絡(luò)STA-WNN 進(jìn)行離線訓(xùn)練，得到確定的小波神經(jīng)網(wǎng)絡(luò)模型，用于描述極譜信號(hào)與多金屬離子濃度間的關(guān)系；最后將訓(xùn)練好的網(wǎng)絡(luò)模型直接用于多金屬離子濃度的同時(shí)測(cè)定，根據(jù)檢測(cè)的極譜信號(hào)實(shí)時(shí)地一次性解析出多金屬離子的質(zhì)量濃度。

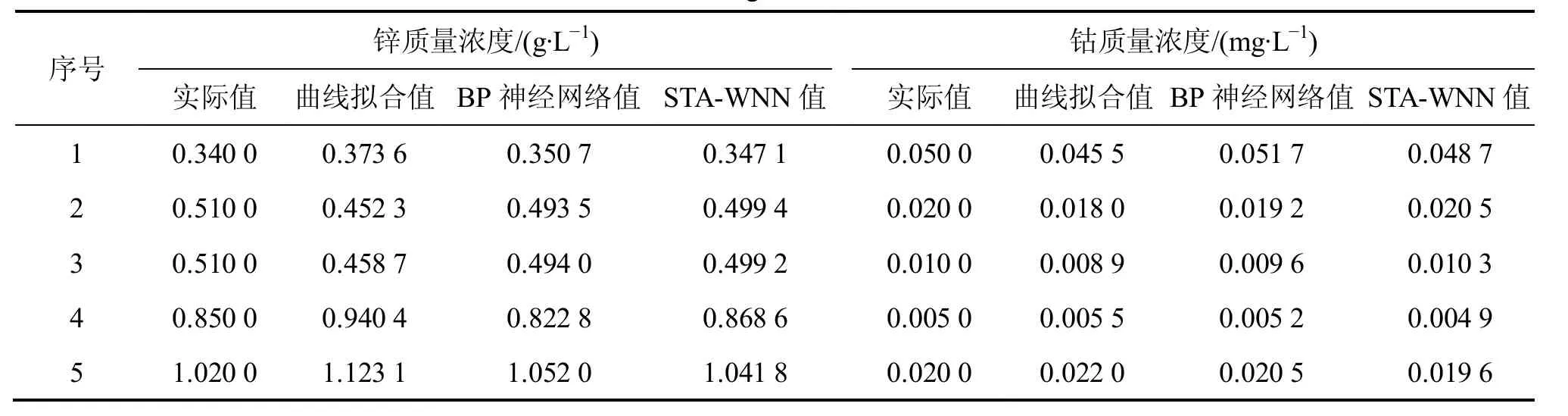
表5　曲線擬合、BP神經(jīng)網(wǎng)絡(luò)、STA-WNN的測(cè)試結(jié)果Table1　Results ofCurve fitting,BP neural network and STA-WNN

采用本文所提出的 STA-WNN 進(jìn)行訓(xùn)練和測(cè)試，并與采用傳統(tǒng)的高斯曲線擬合法[22]和 BP 神經(jīng)網(wǎng)絡(luò)算法所得到的結(jié)果進(jìn)行對(duì)比。BP神經(jīng)網(wǎng)絡(luò)算法和本文所提出的STA-WNN算法的迭代次數(shù)均為1000次，狀態(tài)轉(zhuǎn)移算法中的參數(shù)α取值為從1到1×10?4線性遞減，β，γ和δ 都取固定值1。3種方法應(yīng)用結(jié)果對(duì)比如表5所示。從表5可以看出STA-WNN較其他2種方法具有更高的測(cè)試精度；STA-WNN 對(duì)測(cè)試集中鋅離子的平均測(cè)定誤差為 2.12%，鈷離子的平均測(cè)定誤差為 2.01%，均低于高斯曲線擬合法和 BP 神經(jīng)網(wǎng)絡(luò)算法的平均測(cè)定誤差，說(shuō)明本文提出的方法對(duì)于使用極譜法進(jìn)行多種金屬離子同時(shí)測(cè)定具有較好的應(yīng)用效果。

3　結(jié)論

將狀態(tài)轉(zhuǎn)移算法的全局搜索能力和小波神經(jīng)網(wǎng)絡(luò)強(qiáng)大的擬合能力相結(jié)合，構(gòu)造了基于狀態(tài)轉(zhuǎn)移算法優(yōu)化的小波神經(jīng)網(wǎng)絡(luò)(STA-WNN)，并將其用于極譜法多金屬混合溶液中離子濃度檢測(cè)信號(hào)的在線解析。所提方法的特點(diǎn)在于：

1)針對(duì)極譜信號(hào)的數(shù)據(jù)存在大量冗余問(wèn)題，基于極譜信號(hào)特點(diǎn)及其離子濃度定性分析的基本原理，提取了極譜曲線中有代表性的特征點(diǎn)(即極譜曲線峰值點(diǎn)及其一階導(dǎo)數(shù)極值點(diǎn))作為小波神經(jīng)網(wǎng)絡(luò)的輸入，簡(jiǎn)便了網(wǎng)絡(luò)訓(xùn)練的復(fù)雜度。

2)提取特征點(diǎn)時(shí)，采用離散小波變換得到極譜信號(hào)的一階導(dǎo)數(shù)曲線，由此確定一級(jí)導(dǎo)數(shù)曲線的極值點(diǎn)，從而克服了傳統(tǒng)導(dǎo)數(shù)法放大噪音、一階導(dǎo)數(shù)值不準(zhǔn)確的缺點(diǎn)。

3)結(jié)合改進(jìn)的狀態(tài)轉(zhuǎn)移算法(STA)優(yōu)化確定小波神經(jīng)網(wǎng)絡(luò)參數(shù)，克服傳統(tǒng)小波神經(jīng)網(wǎng)絡(luò)訓(xùn)練方法收斂速度慢、易陷入局部最優(yōu)的不足。所提方法用于鋅濕法冶煉過(guò)程中鋅、鈷離子濃度的同時(shí)測(cè)定，實(shí)驗(yàn)結(jié)果驗(yàn)證了所提方法的有效性。

參考文獻(xiàn)：

[1]李洪桂.濕法冶金學(xué)[M].長(zhǎng)沙: 中南大學(xué)出版社,2005:1?3.LI Honggui.Hydrometallurgy[M].Changsha:Central South University Press,2005:1?3.

[2]王凌云,桂衛(wèi)華,劉梅花,等.基于改進(jìn)在線支持向量回歸的離子濃度預(yù)測(cè)模型[J].控制與決策,2009,24(4): 537?541.WANG Lingyun,GUI Weihua,LIU Meihua,et al.Prediction model of ionConcentration based on improved online support vector regression[J].Control and Decision,2009,24(4): 537?541.

[3]MAHER H M,YOUSSEF R M.Simultaneous determination of ternary drug mixtures using square wave polarography subjected to non-parametric andChermometric peakConvolution[J].Chemometrics and Intelligent Laboratory Systems,2008,94(2): 95?103.

[4]張秀琦,劉輝,鄭建斌,等.信號(hào)處理技術(shù)在重疊化學(xué)信號(hào)解析中的應(yīng)用[J].化學(xué)進(jìn)展,2002,14(3):174?181.ZHANG Xiuqi,LIU Hui,ZHENG Jianbin,et al.The application of signal processing in resolving overlappingChemical bands[J].Progress inChemistry,2002,14(3):174?181.

[5]郝惠敏,湯曉君,白鵬,等.基于核主成分分析和支持向量回歸機(jī)的紅外光譜多組分混合氣體定量分析[J].光譜學(xué)與光譜分析,2008,28(6):1286?1289.HAO Huimin,TANG Xiaojun,BAI Peng,et al.Quantitative analysis of multi-component gas mixture based on KPCA and SVR[J].Spectroscopy and Spectral Analysis,2008,28(6):1286?1289.

[6]ZHANG Xiuqi,ZHENG Jianbin,GAO Hong.Comparison of wavelet transform and Fourier self-deconvolution(FSD)and wavelet FSD forCurve fitting[J].Analyst,2000,125(5): 915?919.

[7]李華,張書(shū)玲,申琦,等.小波分析和偏最小二乘法相結(jié)合用于示波計(jì)時(shí)電位同時(shí)測(cè)定鉛和鉈中的研究[J].計(jì)算機(jī)與應(yīng)用化學(xué),2003,20(1): 27?30.LI Hua,ZHANG Shuling,SHEN Qi,et al.Chronopotiometry using wavelet transform and partial least squares method[J].Computers and AppliedChemistry,2003,20(1): 27?30.

[8]GANG Jiang,HONG Quan,CHENG Wang.A Method to resolve weak and overlapping signals in proton magnetic resonance spectroscopy[C]//2012 InternationalConference on Biomedical Engineering and Biotechnology(iCBEB).Macau,China: IEEE,2012:12?15.

[9]劉思東,張卓勇.人工神經(jīng)網(wǎng)絡(luò)方法用于脈沖極譜重疊峰解析[J].分析化學(xué),1997,25(3): 249?252.LIU Sidong,ZHANG Zhuoyong.Resolution of overlapping pulse differential voltammetric peaks by use of artificial neural network approach[J].Chinese Journal of AnalyticalChemistry,1997,25(3): 249?252.

[10]申金山.基于人工神經(jīng)網(wǎng)絡(luò)的化學(xué)發(fā)光法及光度法在多組分同時(shí)測(cè)定中的應(yīng)用研究[D].成都: 四川大學(xué)輕紡與食品學(xué)院,2005: 85?94.SHEN Jinshan.Studies on simultaneous determination of multi-component byChemiluminescence and spectrophotometry with ANN[D].Chengdu: Sichuan University.College of Light Industry Textile and Food Engineering,2005: 85?94.

[11]王玉田,李長(zhǎng)吾,李艷春,等.基于小波神經(jīng)網(wǎng)絡(luò)的農(nóng)藥熒光光譜識(shí)別[J].計(jì)量學(xué)報(bào),2008,29(1): 84?86.WANG Yutian,LIChangwu,LI Yanchun,et al.Fluorescence spectral recognition of pesticides based on wavelet neural network[J].Acta Metrlogica Sinica,2008,29(1): 84?86.

[12]熊建輝,張普敦,鄭育芳,等.小波神經(jīng)網(wǎng)絡(luò)?遺傳算法用于2-(9-咔唑)乙基氯甲酸酯衍生化氨基酸的膠束電動(dòng)力學(xué)色譜分離優(yōu)化[J].分析科學(xué)學(xué)報(bào),2004,20(3): 237?240.XIONG Jianhui,ZHANG Pudun,ZHENG Yufang,et al.Wavelet neural network and genetic algorithm for separation optimization of amino acids derivatized with 2-(9-carbazole)ethylChloroformate by micellar electrokineticChromatography[J].Journal of Analytical Science,2004,20(3): 237?240.

[13]GUTIéRREZ J M,GUTéS A,CéSPEDES F,et al.Wavelet neural networks to resolve the overlapping signal in the voltammetric determination of phenolicCompounds[J].Talanta,2008,76(2): 373?381.

[14]鮑立威,何敏,沈平.關(guān)于 BP 模型的缺陷的討論[J].模式識(shí)別與人工智能,1995,8(1):1?5.BAO Liwei,HE Min,SHEN Ping.Argument on the shortcoming of BP-model[J].PR & AI,1995,8(1):1?5.

[15]ZHOU Xiaojun,YANGChunhua,GUI Weihua.Initial version of state transition algorithm[C]//2011Second InternationalConference on Digital Manufacturing and Automation(ICDMA).Zhangjiajie,China: IEEE.2011: 644?647.

[16]ZHOU Xiaojun,YANGChunha,GUI Weihua.State transition algorithm[J].Journal of Industrial and Management Optimization,2012,8(4):1039?1056.

[17]姚月季.示波極譜法同時(shí)測(cè)定濕法煉鋅過(guò)程液中銅、 鎘、 鎳[J].冶金分析,1998,18(1): 56?57.YAO Yueji.Simultaneous determination ofCopper,cadmium and nickel in oscillopolarography process using hydrometallurgy[J].Metallurgical Analysis,1998,18(1): 56?57.

[18]肖虹,張曉麗,謝宜羚,等.示波極譜法同時(shí)測(cè)定尿中鉛和鎘[J].理化檢驗(yàn):化學(xué)分冊(cè),2009,44(12):1225?1226.XIAO Hong,ZHANG Xiaoli,XIE Yiling,et al.Simultaneous determination of lead andCadmium in urine by oscilloscopic polarography[J].Ptca(Part B:Chem Anal),2009,44(12):1225?1226.

[19]GAO Xieping.AComparative research on wavelet neural networks[C]//Proceedings of the 9th InternationalConference on Neural Information Processing,Singapore: IEEE.2002:1699?1703.

[20]LEUNG A K M,CHAU F T,GAO Junbin.Wavelet transform: A method for derivativeCalculation in analyticalChemistry[J].AnalyticalChemistry,1998,70(24): 5222?5229.

[21]ZHONG Hongbo,ZHANG Jun,GAO Min,et al.The discrete wavelet neural network and its application in oscillographicChronopotentiometric determination[J].Chemometrics and Intelligent Laboratory Systems,2001,59(1): 67?74.

[22]唐沖,惠輝輝.基于 Matlab 的高斯曲線擬合求解[J].計(jì)算機(jī)與數(shù)字工程,2013,41(8):1262?1263.TANGCong,HUI Huihui.GaussianCurve fitting solution based on matlab[J].Computer & Digital Engineering,2013,41(8):1262?1263.

(編輯 陳燦華)

Online analysis on polarographic detection signal of multi-metal ionConcentrations based on improved wavelet neural networks

WANG Yalin,HUANG Kaihua,HUANG Tianhong,ZHOU Xiaojun,YANGChunhua
(School of Information Science and Engineering,Central South University,Changsha 410083,China)

Abstract:For solving the overlapping peaks problem in multi-component detection of zinc hydrometallurgical process,an online analysis method for polarographic detection signal of multi-metal ionConcentrations was proposed based on the improved wavelet neural network.Firstly,the first derivative of polarographic signal was obtained through the discrete wavelet transform,andConsequently,theCorrespond feature points were obtained as the input of wavelet neural network based on the original signal and the first derivative of polarographic signal.Secondly,an improved state transition algorithm was proposed to optimize the parameters of wavelet neural network(WNN),and then the optimized WNN was adopted to describe the relationship between those feature points and the multi-metal ionConcentrations so that itCould be used to analyze online the polarographic detection signal of multi-metal ionConcentrations.The method was verified by the actual polarographic overlapping peaks signal of zinc andCobalt.The results show that the proposed method is superior to those of theConventionalCurve fitting and the BP neural network algorithm.

Key words:polarographicCurve? multi-metal ionConcentrations? wavelet neural networks(WNN)? state transition algorithm(STA)

中圖分類號(hào)：TP183

文獻(xiàn)標(biāo)志碼：A

文章編號(hào)：1672?7207(2016)01?0100?08

DOI:10.11817/j.issn.1672-7207.2016.01.015

收稿日期：2015?02?10；修回日期：2015?04?08

基金項(xiàng)目(Foundation item)：國(guó)家自然科學(xué)基金資助項(xiàng)目(61273187)；國(guó)家科技支撐計(jì)劃項(xiàng)目(2012BAF03B05)；教育部博士點(diǎn)基金(優(yōu)先發(fā)展領(lǐng)域)資助項(xiàng)目(20110162130011)(Project(61273187)supported by the National Natural Science Foundation ofChina? Project(2012BAF03B05)supported by the National Science & Technology Pillar Program? Project(20110162130011)supported by the Ph.D Programs Foundation of Ministry of Education ofChina)

通信作者：王雅琳，博士，教授，從事復(fù)雜過(guò)程建模、優(yōu)化與控制研究；E-mail: ylwang@csu.edu.cn