基于 Newmark格式的車輛?軌道耦合迭代過程的改進(jìn)算法

張斌，雷曉燕，羅雁云(.同濟(jì)大學(xué) 鐵道與城市軌道交通研究院，上海，0804；.華東交通大學(xué) 鐵路環(huán)境振動(dòng)與噪聲教育部工程研究中心，江西 南昌，33003)

?

基于 Newmark格式的車輛?軌道耦合迭代過程的改進(jìn)算法

張斌1,2，雷曉燕2，羅雁云1
(1.同濟(jì)大學(xué) 鐵道與城市軌道交通研究院，上海，201804；
2.華東交通大學(xué) 鐵路環(huán)境振動(dòng)與噪聲教育部工程研究中心，江西 南昌，330013)

摘要：針對(duì)車輛?軌道耦合系統(tǒng)振動(dòng)方程聯(lián)立求解過程，考慮車輛和軌道2個(gè)子系統(tǒng)模型，提出一種將有限元法和非線性接觸理論相結(jié)合的交叉迭代數(shù)值改進(jìn)算法。該算法將子系統(tǒng)方程非荷載項(xiàng)矩陣進(jìn)行修正和求逆的預(yù)處理，基于Newmark-β積分格式規(guī)則，構(gòu)造具有較高收斂速度及精度的松弛因子函數(shù)和收斂準(zhǔn)則函數(shù)，利用輪軌相互作用力在車輛系統(tǒng)與軌道系統(tǒng)之間的快速交叉迭代，改進(jìn)并實(shí)現(xiàn)輪軌耦合關(guān)系的求解。研究結(jié)果表明：提出的算法正確、有效，極大地提高了動(dòng)力學(xué)方程數(shù)值計(jì)算效率；時(shí)間步長(zhǎng)對(duì)系統(tǒng)數(shù)值解的穩(wěn)定性影響顯著，松弛因子的合理選擇，可起到加速系統(tǒng)迭代和增強(qiáng)迭代穩(wěn)定性的作用；該算法在解決大型工程振動(dòng)問題時(shí)更具高效求解的優(yōu)越性。

關(guān)鍵詞：耦合動(dòng)力學(xué)；輪軌相互作用；Newmark-β法；交叉迭代過程；數(shù)值穩(wěn)定性

列車?軌道相互作用關(guān)系一直是車輛動(dòng)力學(xué)和軌道結(jié)構(gòu)振動(dòng)研究中最重要的基礎(chǔ)性問題，近幾十年來，輪軌間作用力引起的機(jī)車車輛、軌下基礎(chǔ)、橋梁及大地的振動(dòng)等研究課題十分活躍[1?5]，繁簡(jiǎn)程度不一的輪軌動(dòng)力學(xué)理論、模型、算法及程序紛紛出現(xiàn)，有效解決了軌道交通發(fā)展中一些關(guān)鍵問題，取得了一定的研究成果[6?9]。在各類既有數(shù)值分析方法中，動(dòng)力學(xué)方程時(shí)程積分求解是重要環(huán)節(jié)，用以滿足輪軌界面形成的車輛系統(tǒng)與軌道系統(tǒng)動(dòng)態(tài)耦合的平衡關(guān)系。其中，可采用在每一時(shí)間步長(zhǎng)內(nèi)形成車輛?軌道整體動(dòng)力方程，利用直接積分法統(tǒng)一完成求解，計(jì)算穩(wěn)定性好，但輪軌接觸剛度矩陣隨車輛位置變化而變化，其在整體剛度矩陣中元素的位置和量值具有時(shí)變性，矩陣修正及求逆運(yùn)算是制約輪軌耦合問題求解效率的根本因素；也可采用分別建立車輛和軌道系統(tǒng)各自的運(yùn)動(dòng)平衡方程，以車輪與鋼軌之間位移協(xié)調(diào)或者輪軌力差值作為收斂條件進(jìn)行方程求解[10?14]，但兩子系統(tǒng)間耦合的有效性、收斂過程的可控性等許多問題仍值得進(jìn)一步深入探討。在此，本文作者提出一種基于有限元法與非線性接觸理論的改進(jìn)交叉迭代算法，將車輛和軌道兩子系統(tǒng)方程非荷載項(xiàng)矩陣進(jìn)行預(yù)處理，同時(shí)簡(jiǎn)化輪軌界面參數(shù)傳遞與協(xié)調(diào)適應(yīng)條件，交叉迭代過程控制參數(shù)減少至輪軌作用力一項(xiàng)。通過研究時(shí)程積分步長(zhǎng)、收斂精度對(duì)軌道結(jié)構(gòu)振動(dòng)響應(yīng)的影響，論證此算法在準(zhǔn)確性、穩(wěn)定性及編程求解效率方面的優(yōu)越性，為分析機(jī)車車輛與線路相互作用問題提供一種高效數(shù)值計(jì)算方法。

1　車輛系統(tǒng)動(dòng)力學(xué)方程的建立

車輛系統(tǒng)離散為附有二系懸掛的多剛體系統(tǒng)整車模型，如圖1所示，取以線路橫向?qū)ΨQ的半結(jié)構(gòu)研究，考慮車體和轉(zhuǎn)向架的沉浮運(yùn)動(dòng)和點(diǎn)頭運(yùn)動(dòng)，車輪僅考慮沉浮運(yùn)動(dòng)，整車模型共有10個(gè)自由度，規(guī)定位移和力的方向以豎直向上為正，轉(zhuǎn)角和力矩的方向以反時(shí)針為正。

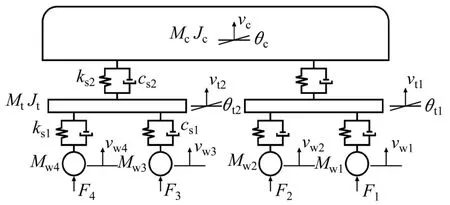
圖1　整車附有二系懸掛系統(tǒng)車輛模型Fig.1　Vertical model of vehicle with primary and secondary suspensions

圖1中，Mc和 Jc分別為車體質(zhì)量與轉(zhuǎn)動(dòng)慣量；Mt和Jt分別為轉(zhuǎn)向架質(zhì)量與轉(zhuǎn)動(dòng)慣量；Mwi(i=1,2,3,4)為第i個(gè)車輪質(zhì)量；ks1和cs1分別為車輛一系懸掛剛度與阻尼；ks2和Cs2分別為車輛二系懸掛剛度與阻尼；vc和vti(i=1,2)分別為車體和前后轉(zhuǎn)向架的沉浮運(yùn)動(dòng)豎向位移；θc和θti(i=1,2)分別為車體和前后轉(zhuǎn)向架的點(diǎn)頭運(yùn)動(dòng)角位移；vwi(i=1,2,3,4)為第i個(gè)車輪的豎向位移；l1和l2分別為車輛固定軸距之半和車輛定距之半。

定義車輛系統(tǒng)的位移向量為

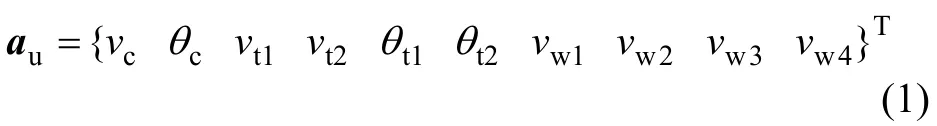
由Hamilton 原理[15]可得車輛系統(tǒng)振動(dòng)方程

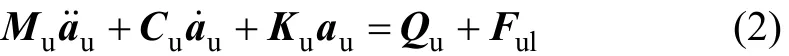
其中：Mu，Cu和 Ku分別為車輛系統(tǒng)質(zhì)量、阻尼和剛度矩陣；，和 au分別為車輛系統(tǒng)加速度、速度和位移向量；Qu為車輛系統(tǒng)重力向量；Ful為軌道系統(tǒng)對(duì)車輛系統(tǒng)的作用力向量。

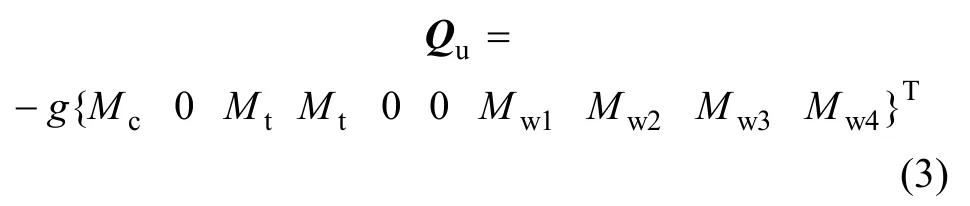
式中：g為重力加速度。

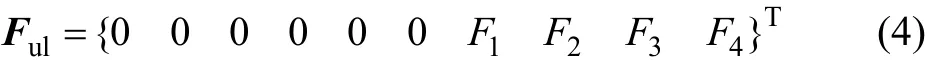
式中：Fi(i=1,2,3,4)為輪軌相互作用力，可用Hertz接觸公式[16]計(jì)算如下

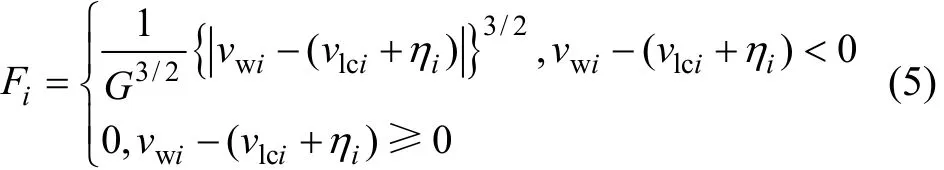
其中：vlci和ηi(i=1,2,3,4)分別為第i個(gè)輪軌接觸處鋼軌位移和軌道不平順值；G 為接觸撓度系數(shù)，錐形踏面車輪 G 為 4.57r?0.149×10?8(m/N 2/3)，磨耗形踏面車輪G為3.86r?0.115×10?8(m/N 2/3)；r為車輪半徑(m)。

2 軌道系統(tǒng)動(dòng)力學(xué)方程的建立

軌道系統(tǒng)亦取半結(jié)構(gòu)研究，板式無(wú)砟軌道單元有限元模型如圖2所示，鋼軌離散為黏彈性點(diǎn)支承梁?jiǎn)卧A(yù)制軌道板和水硬性混凝土支承層離散為連續(xù)黏彈性支承梁?jiǎn)卧？v向相鄰扣件間距為一個(gè)單元，單元長(zhǎng)度記為l，圖2中u1和u4分別為鋼軌的豎向位移；θ1和θ4分別為鋼軌的轉(zhuǎn)角；u2和u5分別為預(yù)制軌道板的豎向位移；θ2和θ5分別為預(yù)制軌道板的轉(zhuǎn)角；u3和u6分別為水硬性混凝土支承層的豎向位移；θ3和θ6分別為水硬性混凝土支承層的轉(zhuǎn)角；ky1，ky2和 ky3分別為無(wú)砟軌道扣件、CA 砂漿和防水層的剛度；cy1，cy2和cy3分別為無(wú)砟軌道扣件、CA砂漿和防水層的阻尼。

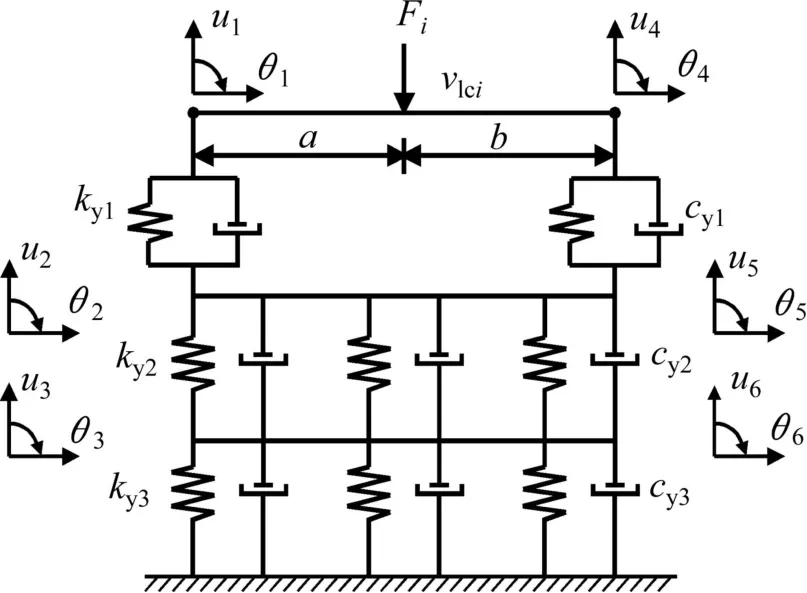
圖2板式無(wú)砟軌道單元模型Fig.2Finite element model of slab track

定義板式無(wú)砟軌道單元的節(jié)點(diǎn)位移向量為

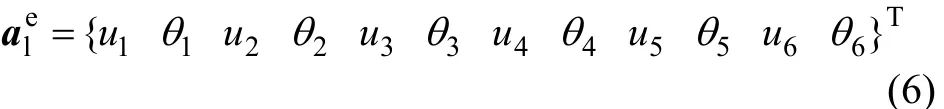
板式無(wú)砟軌道單元的剛度矩陣可表示為

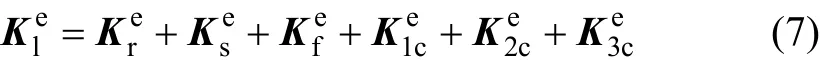
板式無(wú)砟軌道單元的質(zhì)量矩陣可表示為

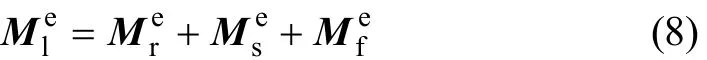
板式無(wú)砟軌道單元的阻尼矩陣可表示為

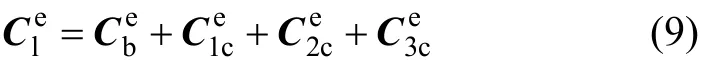
無(wú)砟軌道單元等效節(jié)點(diǎn)荷載向量為

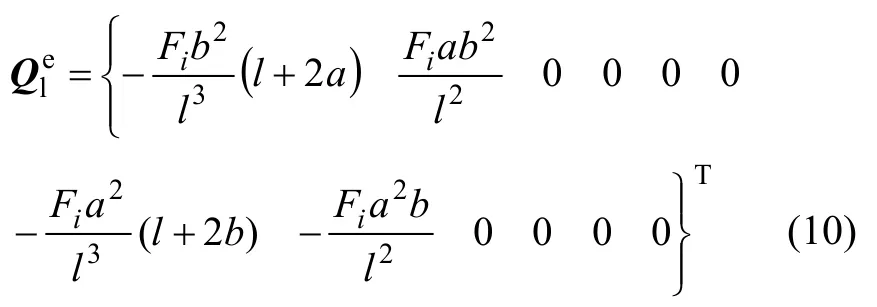
其中：Fi計(jì)算見式(5)；l=a+b。當(dāng)車輪不作用于該軌道單元時(shí)，為12×1階零向量。

根據(jù)上述軌道單元模型，利用有限元“對(duì)號(hào)入座法”組集軌道單元質(zhì)量、阻尼、剛度矩陣和等效荷載向量，可得軌道系統(tǒng)振動(dòng)方程為

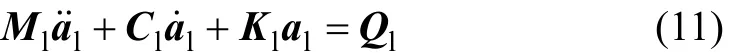
其中：Ml，Cl和Kl分別為軌道系統(tǒng)質(zhì)量、阻尼和剛度矩陣；，和al分別為軌道系統(tǒng)加速度、速度和位移向量；Ql為軌道系統(tǒng)等效荷載向量。，，，。

3　耦合方程求解算法的改進(jìn)

研究和實(shí)踐經(jīng)驗(yàn)表明[12?14]：采用交叉迭代算法求解車輛?軌道非線性耦合系統(tǒng)振動(dòng)方程的關(guān)鍵在于迭代過程的穩(wěn)定性，即在控制精度范圍內(nèi)系統(tǒng)時(shí)程響應(yīng)始終是收斂的。基于Newmark-β積分格式規(guī)則的改進(jìn)交叉迭代法求解耦合系統(tǒng)振動(dòng)方程的推導(dǎo)過程及步驟如下。

3.1計(jì)算準(zhǔn)備

按照Newmark積分法格式，對(duì)2系統(tǒng)中要求解的二階常微分方程組進(jìn)行方程轉(zhuǎn)化。

對(duì)于車輛系統(tǒng)運(yùn)動(dòng)方程(2)，在t+Δt時(shí)刻可寫成如下形式：

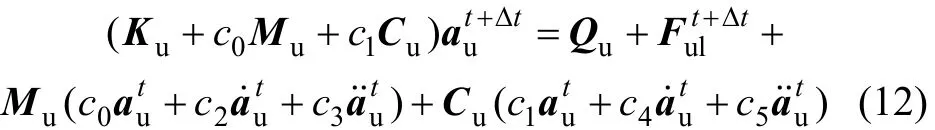
對(duì)軌道系統(tǒng)運(yùn)動(dòng)方程(11)，在 t+Δt 時(shí)刻可寫成如下形式：

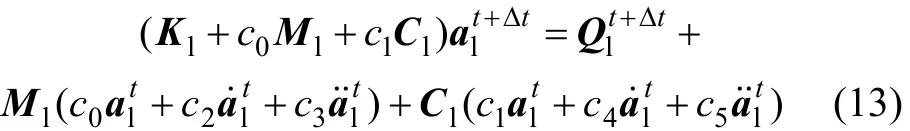
其中：積分常數(shù)α=0.25，δ=0.5，c0=1/(αΔt 2)，c1=δ/(αΔt)，c2=1/(αΔt)，c3=1/(2α)?1，c4=δ/α?1，c5=Δt(δ/α?2)/2，C6=Δt(1?δ)，c7=δΔt。

將式(12)和式(13)中方程左邊部分形成各自等效剛度矩陣，即

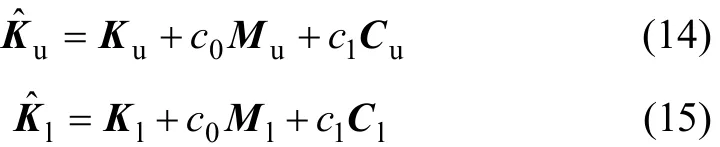
式(14)和式(15)在系統(tǒng)求解中具有非時(shí)變性，在此完成矩陣求逆，整個(gè)數(shù)值求解過程中只需要這樣1次求逆，將其存儲(chǔ)為 Ru和 Rl矩陣，每一時(shí)間步直接調(diào)用即可。

3.2時(shí)間步長(zhǎng)循環(huán)

首先，從t時(shí)刻進(jìn)入t+Δt時(shí)刻時(shí)，系統(tǒng)所有變量初值取t時(shí)刻的最終值，

令

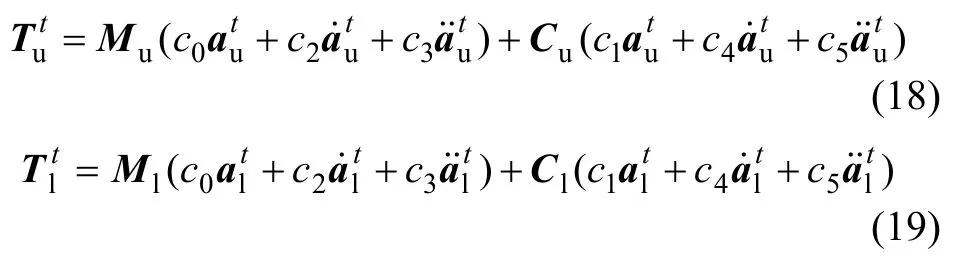
同時(shí)結(jié)合式(16)和式(17)，則車輛系統(tǒng)方程式(12)和軌道系統(tǒng)方程式(13)可簡(jiǎn)化為：

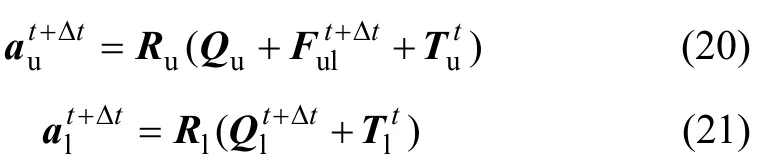
根據(jù)積分格式，2 系統(tǒng)相應(yīng)的速度和加速度可寫成如下形式：

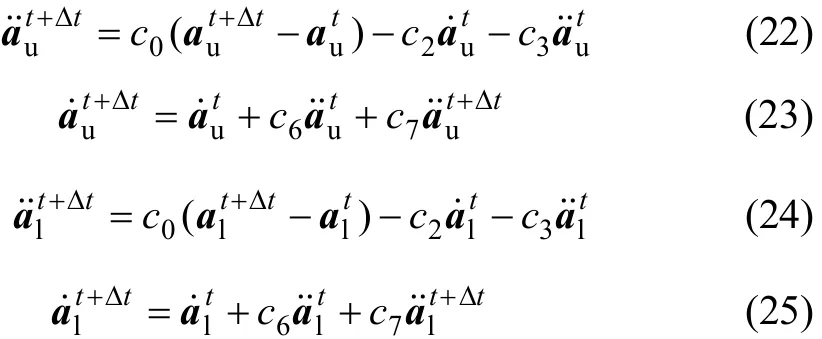
從式(20)和式(21)可以看出：車 輛系統(tǒng)和軌道系統(tǒng)之間協(xié)調(diào)條件的控制參數(shù)僅為輪軌作用力一項(xiàng)，很大程度上簡(jiǎn)化了輪軌界面參數(shù)傳遞過程，2 系統(tǒng)只需進(jìn)行輪軌相互作用力的交叉迭代求解，即可滿足該時(shí)刻系統(tǒng)的收斂條件。這里，設(shè)在t+Δt時(shí)刻，已進(jìn)行k次迭代，現(xiàn)考察第k+1次迭代：

步驟2：利用松弛法，令

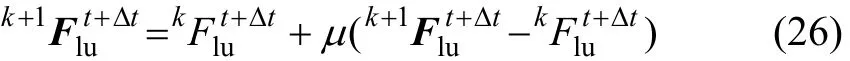
其中：μ為松弛因子，一般取0＜μ＜1，例如μ=0.2～0.4可取得較好效果。

步驟 7：利用軌道位移進(jìn)行收斂性判別，計(jì)算差值：

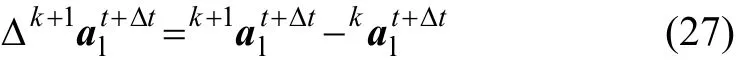
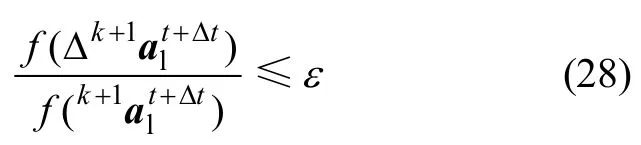
步驟 8：若收斂性得到滿足，則轉(zhuǎn)入下一時(shí)刻進(jìn)行計(jì)算，直至整個(gè)時(shí)域T。

或若收斂性不滿足，令 k=k+1，則轉(zhuǎn)入步驟1，繼續(xù)迭代計(jì)算。

從計(jì)算步驟可以看出：算法思路清晰易懂，積分過程化繁為簡(jiǎn)，編程計(jì)算效率高。與整體動(dòng)力方程統(tǒng)一求解方法相比，交叉迭代法避免了每一時(shí)間步整體剛度矩陣的重新生成和求逆，尤其當(dāng)矩陣維數(shù)較大時(shí)，顯著地減少了計(jì)算工作量。同時(shí)，改進(jìn)后的算法對(duì)振動(dòng)系統(tǒng)收斂過程的控制效果改善明顯，是一種求解車輛?軌道動(dòng)力學(xué)問題的快速數(shù)值分析方法。耦合方程求解算法的程序框圖如圖3所示。，

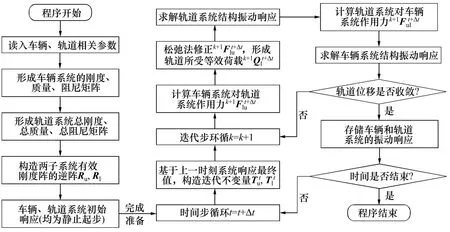
圖3　交叉迭代改進(jìn)算法計(jì)算流程Fig.3　Calculation flow of the improved staggered iterative algorithm

4 算例分析

4.1算法驗(yàn)證

為驗(yàn)證本文提出的交叉迭代改進(jìn)算法的正確性，與向俊等[17]提出的橫向有限條與無(wú)砟軌道板段單元的車軌系統(tǒng)豎向振動(dòng)分析法進(jìn)行算例比較，計(jì)算條件為高速列車(1動(dòng)+4拖)以200 km/h 速度在板式軌道上運(yùn)行，取波長(zhǎng)為12.5 m、波幅為3 mm的周期性正弦函數(shù)為軌道高低不平順激振源，比較 2種方法的計(jì)算結(jié)果。采用本文算法計(jì)算結(jié)果分別如圖4～9所示。

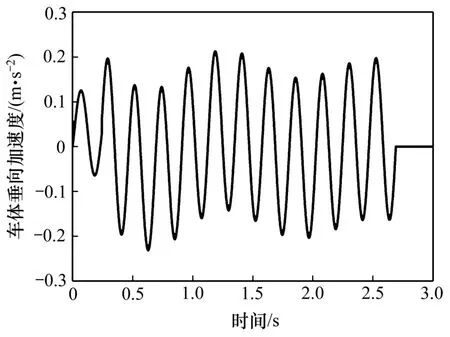
圖4動(dòng)車車體垂向加速度時(shí)程Fig.4Time history of vertical acceleration of motor vehicle body

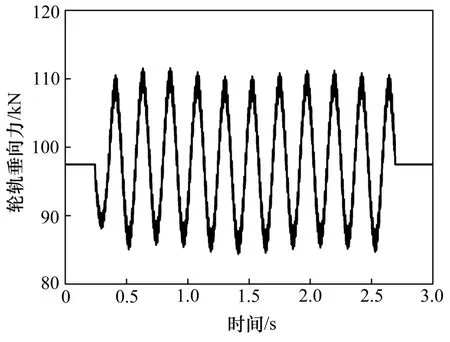
圖5　動(dòng)車輪軌垂向力時(shí)程Fig.5　Time history of wheel/rail force of motor vehicle

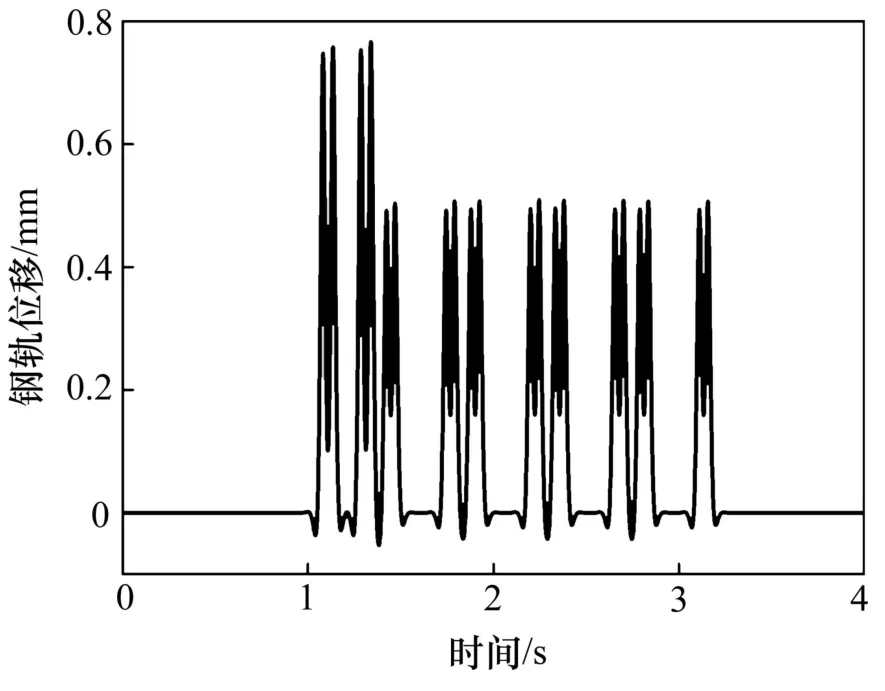
圖6　鋼軌垂向位移時(shí)程Fig.6　Time history of vertical displacement of rail

圖7　鋼軌垂向加速度時(shí)程Fig.7　Time history of vertical acceleration of rail

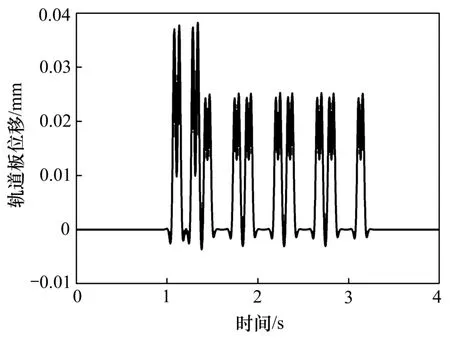
圖8　軌道板垂向位移時(shí)程Fig.8　Time history of vertical displacement of slab

圖9　軌道板垂向加速度時(shí)程Fig.9　Time history of vertical acceleration of slab

從圖4～9可以看出：各響應(yīng)波形符合物理概念，與向俊等[17]計(jì)算得到的系統(tǒng)動(dòng)力響應(yīng)幅值與變化規(guī)律基本一致，證明了本文算法的有效性和可行性。

此外，系統(tǒng)某一時(shí)刻(t時(shí)刻)拖車輪軌相互作用力和相應(yīng)輪軌接觸處鋼軌位移的迭代收斂過程，分別如圖10 和圖11所示。從圖10和圖11可見：耦合系統(tǒng)以上一時(shí)刻(t?Δt 時(shí)刻)平衡狀態(tài)為初值，經(jīng)過若干次迭代，逐步在該時(shí)刻(t時(shí)刻)達(dá)到新的平衡狀態(tài)。

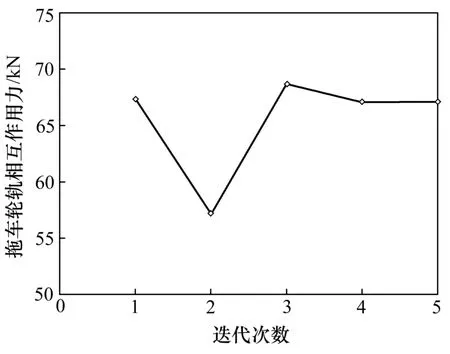
圖10　t時(shí)刻拖車輪軌力迭代過程Fig.10　Iterative process of wheel/rail force of trailer at t moment

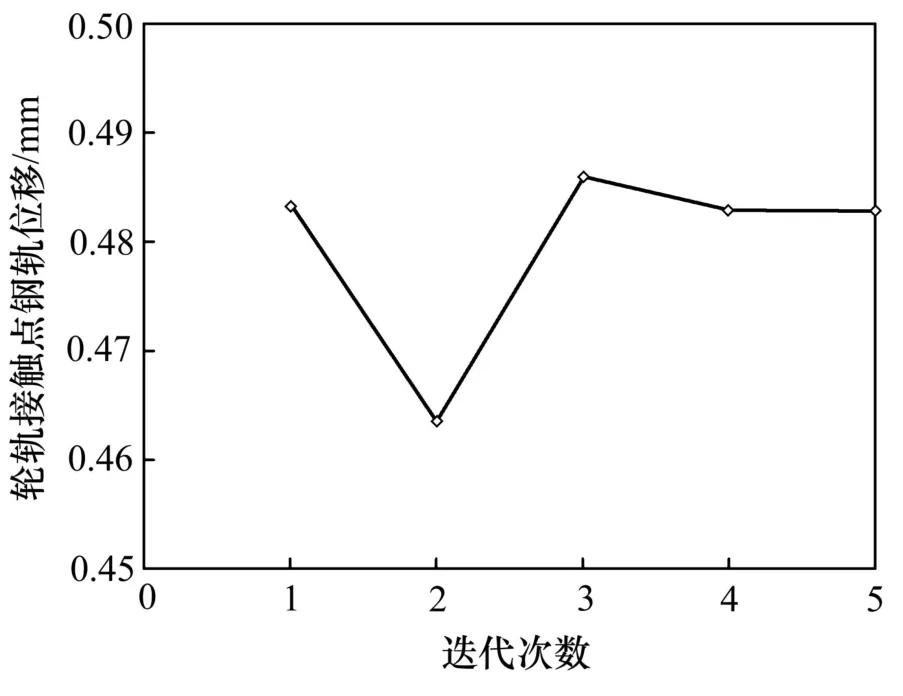
圖11　t時(shí)刻輪軌接觸點(diǎn)鋼軌位移迭代過程Fig.11　Iterative process of rail displacement of wheel/railContact point at t moment

4.2時(shí)間步長(zhǎng)的影響

時(shí)間步長(zhǎng)Δt分別選取0.05，0.10，0 .50及1.00 ms，考察時(shí)間步長(zhǎng)對(duì)系統(tǒng)方程求解過程的影響。其中：車輛選用CRH3型動(dòng)車，CRTSⅡ型板式軌道，行車速度為250 km/h，收斂精度設(shè)置為1.0×10?7。這里約定，每一時(shí)間步內(nèi)軌道系統(tǒng)方程和車輛系統(tǒng)方程各自分別完成1次求解記為耦合系統(tǒng)1次交叉迭代，每一工況迭代次數(shù)按照耦合系統(tǒng)求解過程中最大迭代次數(shù)統(tǒng)計(jì)。不同時(shí)間步長(zhǎng)時(shí)系統(tǒng)的迭代次數(shù)計(jì)算結(jié)果如表1所示。

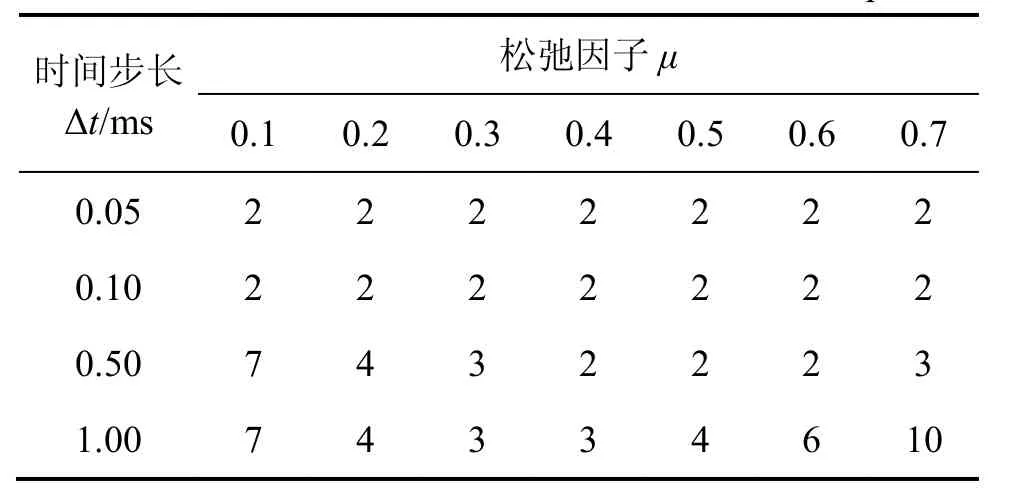
表1　不同時(shí)間步長(zhǎng)系統(tǒng)迭代次數(shù)Table1　Number of iterations at different time steps

從表1可以看出：時(shí)間步長(zhǎng)越小，系統(tǒng)下一時(shí)刻的狀態(tài)越接近上一時(shí)刻系統(tǒng)的平衡狀態(tài)，很容易再次達(dá)到平衡位置，因而系統(tǒng)迭代次數(shù)少，收斂速度快，且松弛因子對(duì)系統(tǒng)求解的影響逐漸降低，但是計(jì)算效率低下，此時(shí)，配合松弛因子，適當(dāng)增大時(shí)間步長(zhǎng)，可有效提高求解效率。例如，計(jì)算時(shí)間取1s，比較μ=0.3，時(shí)間步長(zhǎng)Δt從0.5 ms減小到0.1ms，耦合系統(tǒng)求解效率。當(dāng) Δt=0.5 ms 時(shí)，系統(tǒng)總迭代次數(shù)為1/0.000 5×(2×78%+3×22%)=4 440次，其中：2和3為該工況包含的迭代次數(shù)，78%和 22%為各自比例，同理，Δt=0.1ms 時(shí)，系統(tǒng)總迭代次數(shù)為1/0.0001× 2×100%=20 000次，后者為前者的4.5倍，求解效率大大降低，因此松弛因子的使用可以選取更大的時(shí)間步長(zhǎng)，增強(qiáng)求解時(shí)間的經(jīng)濟(jì)性。

然而，時(shí)間步長(zhǎng)取得較大時(shí)，系統(tǒng)將嚴(yán)重偏離上一時(shí)刻平衡狀態(tài)，喪失穩(wěn)定性，導(dǎo)致系統(tǒng)數(shù)值解的發(fā)散而最終無(wú)法收斂。因此，對(duì)于相互作用的復(fù)雜非線性車軌耦合問題，Newmark數(shù)值積分法不再是無(wú)條件穩(wěn)定的，也會(huì)產(chǎn)生數(shù)值不穩(wěn)定性現(xiàn)象。

4.3收斂精度的影響

收斂精度ε分別選取1.0×10?7，1.0×10?8，1.0×10?9及1.0×10?10，考慮有砟軌道和無(wú)砟軌道2種軌道類型，探討收斂精度對(duì)不同軌道結(jié)構(gòu)動(dòng)力響應(yīng)的影響。其中：車輛選用CRH3型動(dòng)車，軌道參數(shù)分別采用鐵路干線軌道設(shè)計(jì)參數(shù)[14]和CRTSⅡ型板式軌道參數(shù)[6]，行車速度取250 km/h。不同收斂精度對(duì)振動(dòng)系統(tǒng)的影響如圖12所示。

從圖12可見：無(wú)砟軌道耦合系統(tǒng)的迭代次數(shù)普遍比有砟軌道的多，原因是無(wú)砟軌道單元模型較有砟軌道單元模型位移自由度更多，矩陣維數(shù)隨之增加引起的，但是在松弛因子位于 0.2～0.4 區(qū)間時(shí)，兩者迭代次數(shù)差別不大，且均有明顯減少趨勢(shì)。同時(shí)，收斂精度要求越高，系統(tǒng)迭代次數(shù)也越多，然而在松弛因子0.3附近，迭代次數(shù)并沒有隨收斂精度提高而增加。因而，松弛因子的合理選擇，有助于耦合系統(tǒng)的加速迭代。

此外，收斂精度對(duì)系統(tǒng)的動(dòng)力響應(yīng)具有顯著影響，圖13 和圖14 所示分別為當(dāng)收斂精度為1.0×10?7和1.0×10?10時(shí)，有砟軌道系統(tǒng)的輪軌相互作用力時(shí)程，此時(shí)松弛因子取0.1。從圖13和圖14可見：輪軌力理論值為 70 kN，計(jì)算機(jī)程序固有相對(duì)誤差最大為2%～3%，因此，一般動(dòng)力學(xué)分析，收斂精度在1.0×10?7～1.0×10?10之間均可滿足計(jì)算要求，對(duì)于精細(xì)化分析則需采用較高的收斂精度。當(dāng)此工況松弛因子取0.3時(shí)，不同收斂精度間系統(tǒng)動(dòng)力響應(yīng)差別不明顯，反映出松弛因子起增強(qiáng)迭代穩(wěn)定性的作用。

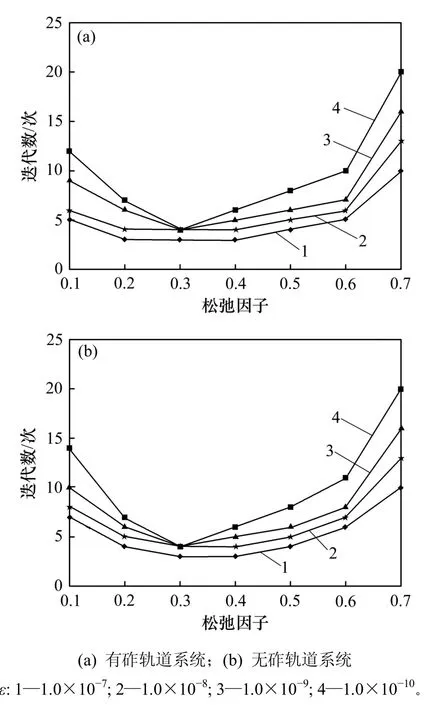
圖12收斂精度對(duì)振動(dòng)系統(tǒng)的影響Fig.12Influence ofConvergence precision on vibration systems

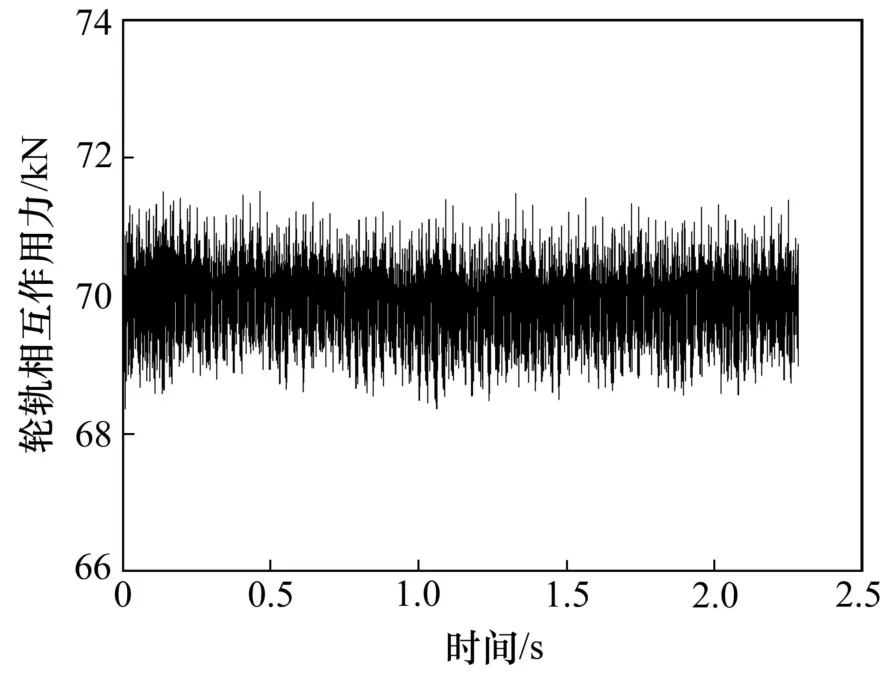
圖13　收斂精度1.0×10?7時(shí)輪軌作用力時(shí)程Fig.13　Time history of wheel/rail force at1.0×10 ?7Convergence precision

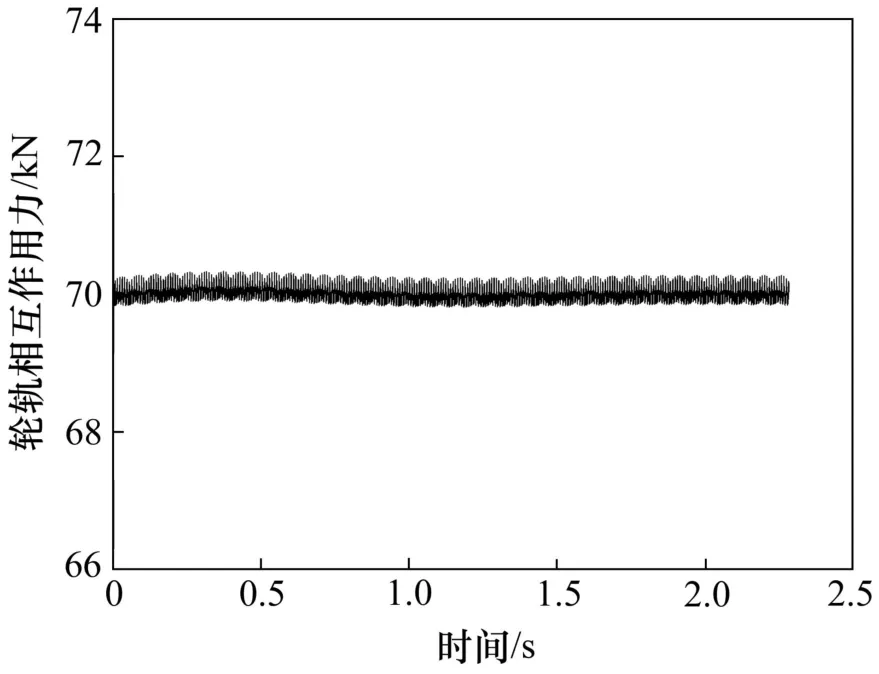
圖14收斂精度1.0×10?10時(shí)輪軌作用力時(shí)程Fig.14Time history of wheel/rail force at1.0×10 ?10Convergence precision

5 結(jié)論

1)提出基于 Newmark-β 積分格式的交叉迭代改進(jìn)數(shù)值計(jì)算方法。算例對(duì)比分析高速列車通過板式軌道時(shí)車輛系統(tǒng)和軌道系統(tǒng)的動(dòng)力響應(yīng)，驗(yàn)證了算法的正確性。

2)交叉迭代改進(jìn)算法對(duì)耦合方程的積分初值問題和收斂問題引入松弛因子函數(shù)，加速系統(tǒng)迭代的同時(shí)增強(qiáng)迭代穩(wěn)定性，較好地反映輪軌相互作用引起的系統(tǒng)動(dòng)力學(xué)響應(yīng)特征，顯著地提高積分求解速度，克服了迭代過程易發(fā)散等弊端。

3)迭代收斂精度可根據(jù)精細(xì)化動(dòng)力學(xué)研究或粗略化工程實(shí)際的需要進(jìn)行設(shè)置，該算法在準(zhǔn)確性、穩(wěn)定性和程序求解效率等方面對(duì)解決大型工程振動(dòng)問題具有較強(qiáng)的適用性。

參考文獻(xiàn)：

[1]RAY WC,JOSEPH P.Dynamic of structures[M].Berkeley:Computers & Structures,Inc.,1995:120?124.

[2]REZAIEE-PAJAND M,ALAMATIAN J.Numerical time integration for dynamic analysis using a new higher order predictor-corrector method[J].EngineeringComputations,2008,25(6): 541?568.

[3]CHENC,RICLES J M.Stability analysis of direct integration algorithms applied to MDOF nonlinear structural dynamics[J].Journal of Engineering Mechanics,2010,136(4): 485?495.

[4]FERIANI A,MULAS M G,ALIPRANDIC.Time domain iterative procedures for vehicle–bridge dynamic interaction[C]//Proceedings of ISMA2006: InternationalConference on Noise and Vibration Engineering.Belgium: Katholieke Universiteit Leuven,2006:1179?1193.

[5]翟婉明.車輛?軌道耦合動(dòng)力學(xué)[M].3版.北京: 科學(xué)出版社,2007:117?124.ZHAI Wanming.Vehicle-trackCoupling dynamics[M].3rd ed.Beijing: Science Press,2007:117?124.

[6]張斌,雷曉燕.基于車輛?軌道單元的無(wú)砟軌道動(dòng)力特性有限元分析[J].鐵道學(xué)報(bào),2011,33(7): 78?85.ZHANG Bin,LEI Xiaoyan.Analysis on dynamic behavior of ballastless track based on vehicle and track elements with finite element method[J].Journal of theChina Railway Society,2011,33(7): 78?85.

[7]朱志輝,余志武,蔣麗忠,等.高速鐵路橋梁及場(chǎng)地土交通振動(dòng)分析[J].振動(dòng)工程學(xué)報(bào),2012,25(5): 548?555.ZHU Zhihui,YU Zhiwu,JIANG Lizhong,et al.Analysis of bridge-ground vibrations induced by moving loads of high-speed train[J].Journal of Vibration Engineering,2012,25(5): 548?555.

[8]史吏,蔡袁強(qiáng),徐長(zhǎng)節(jié).軌道結(jié)構(gòu)動(dòng)力響應(yīng) Newmark 方法時(shí)間積分步長(zhǎng)的確定[J].浙江大學(xué)學(xué)報(bào)(工學(xué)版),2014,48(2): 228?235.SHI Li,CAI Yuanqiang,XUChangjie.Time step length determination of Newmark method for dynamic responses of railway tracks[J].Journal of Zhejiang University(Engineering Science),2014,48(2): 228?235.

[9]徐慶元,李斌,周小林.高速列車作用下路基上板式無(wú)砟軌道動(dòng)力系數(shù)[J].中南大學(xué)學(xué)報(bào)(自然科學(xué)版),2011,42(9): 2831?2836.XU Qingyuan,LI Bin,ZHOU Xiaolin.DynamicCoefficient of slab track system on subgrade under high-speed trains[J].Journal ofCentral South University(Science and Technology),2011,42(9): 2831?2836.

[10]張健,譚述君,吳昌華.車輛?軌道非線性耦合動(dòng)力學(xué)的精細(xì)積分法及其應(yīng)用[J].振動(dòng)與沖擊,2012,31(8): 5?10.ZHANG Jian,TAN Shujun,WUChanghua.A precise integration method for vehicle-track nonlinearCoupling dynamics and its application[J].Journal of Vibration and Shock,2012,31(8): 5?10.

[11]張楠,夏禾.基于全過程迭代的車橋耦合動(dòng)力系統(tǒng)分析方法[J].中國(guó)鐵道科學(xué),2013,34(5): 32?38.ZHANG Nan,XIA He.A vehicle-bridge interaction dynamic system analysis method based on inter-system iteration[J].China Railway Science,2013,34(5): 32?38.

[12]吳定俊,李奇,陳艾榮.車橋耦合振動(dòng)迭代求解數(shù)值穩(wěn)定性問題[J].力學(xué)季刊,2007,28(3): 405?411.WU Dingjun,LI Qi,CHEN Airong.Numerical stability of iteration scheme for solution of vehicle-bridgeCoupling vibration[J].Chinese Quarterly of Mechanics,2007,28(3): 405?411.

[13]YANG Fuheng,FONDER G A.An iterative solution method for dynamic response of bridge-vehicles systems[J].Journal of Earthquake Engineering and Structural Dynamics,1996,25(2):195?215.

[14]雷曉燕.軌道力學(xué)與工程新方法[M].北京: 中國(guó)鐵道出版社,2002: 42?46.LEI Xiaoyan.New methods in railroad track mechanics & technology[M].Beijing:China Railway Publishing House,2002: 42?46.

[15]陳濱.分析動(dòng)力學(xué)[M].2版.北京: 北京大學(xué)出版社,2012: 316?320.CHEN Bin.Analytical dynamics[M].2nd ed.Beijing: Peking University Press,2012: 316?320.

[16]金學(xué)松,劉啟躍.輪軌摩擦學(xué)[M].北京: 中國(guó)鐵道出版社,2004: 51?57.JIN Xuesong,LIU Qiyue.Wheel/rail tribology[M].Beijing:China Railway Publishing House,2004: 51?57.

[17]向俊,赫丹,曾慶元.橫向有限條與無(wú)砟軌道板段單元的車軌系統(tǒng)豎向振動(dòng)分析法[J].鐵道學(xué)報(bào),2007,29(4): 64?69.XIANG Jun,HE Dan,ZENG Qingyuan.Analysis method of vertical vibration of train and ballastless track system with the lateral finite strip and slab segment element[J].Journal of theChina Railway Society,2007,29(4): 64?69.

(編輯 羅金花)

Improved algorithm of iterative process for vehicle-trackCoupled system based on Newmark formulation

ZHANG Bin1,2, LEI Xiaoyan2, LUO Yanyun1
(1.Institute of Railway and Urban Mass Transit,Tongji University,Shanghai 201804,China? 2.Engineering ResearchCenter of Railway Environment Vibration and Noise,Ministry of Education,EastChina Jiaotong University,Nanchang 330013,China)

Abstract:Based on finite element method and nonlinearContact theory,an improved staggered iterative algorithm for the simultaneous solution process of vehicle-track system equations was presented.In the algorithm,the dynamic model was divided into vehicle subsystem and track subsystem.For the non-load matrices in two subsystems wereCarried out some necessary preprocesses such asCorrection and inversion.Based on rules of the Newmark-β integration scheme,the relaxation factor function andConvergenceCriterion function wereConstructed with higherConvergence speed andConvergence precision respectively.To accomplish the solution of the wheel/railCoupled relationship,the fast staggered iteration of wheel/rail interaction force between vehicle subsystem and track subsystem was applied.The results show that the proposed algorithm isCorrect,effective and able to greatly enhance resolution efficiency of the kinetic equationsCompared withConventional integration mode.The time step has tremendous effect on the stability of numerical solution,and the reasonableChoice of relaxation factor plays aCrucial role in accelerating iteration and enhancing the stability of iterative solution.The proposed algorithm is more efficient in large engineering dynamic response.

Key words:Coupling dynamics? wheel/rail interaction? Newmark-β method? staggered iterative process? numerical stability

中圖分類號(hào)：U213.2

文獻(xiàn)標(biāo)志碼：A

文章編號(hào)：1672?7207(2016)01?0298?09

DOI:10.11817/j.issn.1672-7207.2016.01.041

收稿日期：2015?01?29；修回日期：2015?03?29

基金項(xiàng)目(Foundation item)：國(guó)家自然科學(xué)基金資助項(xiàng)目(U1134107,51208198)；江西省自然科學(xué)基金資助項(xiàng)目(20142BAB216001)；江西省教育廳科學(xué)技術(shù)研究項(xiàng)目(GJJ14393)(Projects(U1134107,51208198)supported by the National Nature Science Foundation ofChina? Project(20142BAB216001)supported by the Natural Science Foundation of Jiangxi Province? Project(GJJ14393)supported by the Science and Technology Program of Education Department of Jiangxi Province)

通信作者：雷曉燕，博士，教授，從事鐵路環(huán)境振動(dòng)與噪聲控制研究；E-mail: xiaoyanlei2013@163.com