兩層流中二維箱體結構反射和透射的模擬研究

尚玉超，勾瑩，滕斌，鄭艷娜

(1.大連理工大學 海岸和近海工程國家重點實驗室，遼寧 大連 116024；2.大連海洋大學 海洋與土木工程學院，遼寧 大連 116023)

兩層流中二維箱體結構反射和透射的模擬研究

尚玉超1，勾瑩1，滕斌1，鄭艷娜2

(1.大連理工大學 海岸和近海工程國家重點實驗室，遼寧 大連 116024；2.大連海洋大學 海洋與土木工程學院，遼寧 大連 116023)

摘要：基于兩層流體簡化模型，研究了水面箱型結構在兩層流體中對波浪的反射和透射特性。為研究復雜海洋結構，采用外域級數展開和內域邊界元數值方法相結合的手段建立了頻域數學模型，在外域和內域交界的輻射面上利用連續性條件建立聯立方程組。其中內域計算采用Rankine源作為格林函數，既避免了求解復雜的格林函數，又可直接獲得自由水面及內界面上的速度勢。經過與級數展開的解析方法對比，以及兩層流中波能流守恒的驗證，證明了本文建立的這一聯合數值模型的正確性。利用這一數值模型通過計算反射系數和透射系數的變化情況，研究了兩層流中存在箱型結構時各模態波浪的轉化情況，分析了兩層流中箱型結構的反射和透射特性。

關鍵詞：兩層流體；邊界元方法；Rankine源；反射系數；透射系數；水波；箱型結構

網絡出版地址：http://www.cnki.net/kcms/detail/23.1390.U.20160411.1024.028.html

波浪經過結構物后，透射波浪的能量和波面變化情況是設計關心的主要問題之一。通常的研究都假定海水密度均一，但實際海洋環境中，海水密度在垂向上存在顯著的層化現象。這一特性導致在海洋內部也會產生波動，因此對結構的反射、透射問題都存在顯著的影響[1]。把流體看作密度均勻的兩層，在兩層交接面上密度存在突變，此時波浪會以兩種不同的模態傳播，一種是表面波模態，另一種是內波模態[2]。尤云祥[3]和Dhillon等[4]分別研究了垂直薄板在有限深和無限深兩層流體中的反射及透射特性。Behera等[5]分析了矩形多孔結構在有限深兩層流體中與斜向入射波浪的相互作用問題。本文針對水面固定箱型結構，從反射系數和透射系數的角度出發，通過自由表面和內界面上波面的變化情況研究兩種模態波浪的變化特性。

采用勢流理論求解兩層流中結構的水動力特性時，Kashiwagi等[6]基于邊界元方法，利用滿足自由水面條件和內界面條件的格林函數，計算了二維情況下作用于物體上的激振力以及運動響應特性，并與物理模型試驗結果進行了對比。Nguyen等[7]推導出三維情況下有限水深的兩層流體中滿足自由水面條件和內界面條件的格林函數。計算結果表明，在一定頻率范圍內分層效應對結構物水動力特性有顯著影響，并且當入射波浪以內波模態入射時會在特定頻率范圍內引起方箱較大的轉動。勾瑩等[8]采用簡單格林函數建立了時域方法求解積分方程，對漂浮圓柱、方箱等的水動力特性進行了研究。石強[9]基于分離變量法，建立了大直徑圓柱體和方箱在兩層流體中繞射勢與輻射勢的解析計算方法。Zhang等[11]運用特征函數匹配的方法，研究了兩層流中月池結構垂向振蕩的附加質量和輻射阻尼，以及在共振頻率時自由水面和內界面上的波動情況。

本文采用數值方法和解析方法相結合的研究手段，將流域分為內域和外域兩部分，內域采用利用簡單格林函數的邊界元法求解，外域速度勢及導數利用解析展開式表示。這一模型既能求解任意物體的水動力特性，又避免了求解復雜的滿足自由水面條件的格林函數；同時外域采用解析方法也使無窮遠處的散射條件得到了很好的滿足。通過計算方箱的激振力并與解析方法結果對比，驗證了模型的正確性。根據單層流中波能流守恒原理推導出了兩層流中的波能流守恒關系，利用這一關系對模型的精確性進行了進一步的驗證。最后給出了兩層流體中各模態的反射系數及透射系數的定義，研究了某一模態入射波浪與物體作用后，自由水面及內界面上的波面變化情況。

1數學模型

考慮二維情況下的兩層理想流體，定義直角坐標系OXZ，坐標軸OZ垂直向上，OX與靜水面重合。上層流體的密度和深度分別為ρ1和h1，下層流體的密度和深度分別為ρ2和h2，兩層流體的密度比為γ=ρ1/ρ2，總水深為h=h1+h2。在物體周圍取輻射邊界Sc1和Sc2，將流域分為3部分：內域Ω1、左外域Ω2和右外域Ω3。內域中自由水面、物面、內界面及水底分別表示為Sf、Sb、SI、和Sd，如圖1所示。

圖1　計算域定義Fig.1　Definition sketch of computation domain

1.1入射速度勢

(1)

m=2時，為內波模態入射

(2)

垂向特征函數：

1.2反射和透射速度勢

當入射波作用到結構物上后，會產生反射波和透射波，其速度勢用φd表示，并且滿足以下定解條件。拉普拉斯方程：

(3)

自由水面、內界面(垂向速度連續、壓力連續)和水底邊界條件：

(4)

(5)

(6)

(7)

物面條件：

(8)

另外還有向外傳播的遠場條件，其中，K=ω2/g。

1.2.1外域速度勢

外域反射和透射速度勢用下面級數展開的方式表達[10]，對于左外域：

(9)

對于右外域：

(10)

上述兩式中的前兩項分別為表面波模態和內波模態的傳播項，后兩項分別為表面波模態和內波模態的非傳播項。考慮到非傳播項的衰減性，本文展開式中n都取到有限項N，此時未知系數的個數為2(N+N+2)即4(N+1)。輻射邊界及外域速度勢的求解轉化為求解級數展開式中的有限項系數，這些系數反映了外域中勢函數的組成及其變化規律。

1.2.2內域積分方程

在內域上下兩層流體區域內分別運用格林第二定理，可將問題轉化為邊界積分方程求解。對于上層流體有積分方程：

(11)

對于下層流體有積分方程：

(12)

式中α為固角系數，法線方向均以指出積分區域為正。上層流體取Rankine源為格林函數，下層流體取Rankine源和它關于海底的鏡像作為格林函數，分別表示如下：

在自由水面、物面和內界面積分時，未知量為速度勢，而在輻射面積分時，通過輻射面上內、外域速度勢及其導數的連續性，將未知量轉化為外域速度勢展開式中的系數A和B。最后通過在自由水面、物面、內界面及輻射面劃分網格，對積分方程(11)、(12)分別進行離散可得兩組線性方程組：

(13)

(14)

(15)

2模型的驗證

為驗證所建立模型及求解過程的正確性，以水面固定箱型結構為例，計算了其波浪激振力以及波能流的守恒關系。上層流體水深h1=1.4 m、密度ρ1= 1 000 kg/m3，下層流體水深h2=0.6 m、密度ρ2=1 020 kg/m3,總水深h=2.0 m，方箱半寬B=0.5h=1.0 m，吃水T=0.5h=1.0 m。

2.1網格劃分及收斂性驗證

不同節點數的計算結果如圖2所示。

(a) x1的自功率譜

(b) x2的自功率譜圖2　不同節點數下收斂性分析Fig.2　Convergence test for various node numbers

圖中縱坐標表示表面波模態波浪從左側入射時，自由水面和內界面固定點x=8.5 m處波面升高隨頻率的變化情況。經比較可知，節點數為1 062時數值結果已經收斂。此時自由水面節點數為202，物面節點數為239，內界面節點數為343，上下輻射面分別為178和100。

2.2波浪激振力

(a) 表面波模態

(b) 內波模態圖3　波浪入射時的水平激振力Fig.3　Horizontal exciting force under incident

(a) 表面波模態

(b) 內波模態圖4　波浪入射時的垂向激振力Fig.4　Vertical exciting force under incident

(a) 表面波模態

(b) 內波模態圖5　波浪入射時的繞y軸力矩Fig.5　Exciting force moment under incident

由圖可知，當入射波浪為表面波模態時，水平波浪力、垂向波浪力和繞y軸力矩都與單層流體中作用力基本重合，說明此時激振力基本不受分層效應的影響。當入射波浪為內波模態時，3個方向的作用力在低頻處都有多個極值和零點，并且遠小于表面波模態入射的激振力，隨著頻率的不斷增大，激振力最后都減小為0。

2.3能量守恒關系

根據波能流守恒定理可得：

(16)

式中：Φ2、Φ3分別為左外域和右外域中加入時間因子的速度勢，將速度勢表達式代入式(16)并化簡可得到如下能量守恒關系式：

(17)

式中：m=1代表入射波浪模態為表面波模態，m=2代表入射波浪模態為內波模態。并有如下定義式：

(18)

圖6兩曲線分別為入射波為表面波模態和內波模態時，模型所計算出的能量P隨無因次化頻率的變化關系，可以看出所建立模型能很好地滿足能量守恒關系式(16)，進一步證明了模型的精確性。

圖6　波能流守恒關系數值結果Fig.6　Numerical results of wave energy flow conservation relation

3反射、透射系數的定義與計算結果

(19)

(20)

式中：l=1,2分別代表自由水面和內界面，m=1,2分別代表反射(透射)波浪為表面波模態和內波模態；ηr、ηt和ηi分別為反射波、透射波和入射波波高。入射波為表面波模態時，ηi取自由表面入射波波高；入射波為內波模態時，ηi取內界面入射波波高。

雖然自由水面和內界面上都存在兩種模態的波浪，但是由于自由水面上以表面波模態波浪成分為主，內界面上以內波模態波浪成分為主，因此在后續分析中，只給出自由水面上表面波模態波浪的反透射系數和內界面上內波模態波浪的反透射系數。其余系數可通過關系式(2)確定。

圖7(a)給出了表面波模態波浪入射時，自由水面上表面波模態的反射和透射系數，其中L1為表面波模態波長。可以看出，隨波長的減小自由水面上表面波模態反射系數趨近于1，透射系數趨近于0，趨勢與單層流體一致。圖7(b)給出了表面波模態波浪入射時，內界面上內波模態波浪的反射和透射系數，其中L2為內波模態波長。

(a) 自由水面

(b) 內界面圖7　入射波為表面波模態時自由水面及內界面上　　的反射和透射系數Fig.7　Reflection and transmission coefficients on free-surface 　and interface under incident surface-wave mode

由圖7可知，表面波模態的入射波浪與結構物作用后將在內界面上產生較大幅度的波動，最高可接近自由表面入射波浪波幅的2倍左右。這是因為兩層流體間密度差很小，其恢復力很小，相當于將分層介質置于微重力場，流體受到很小的擾動就會偏離其平衡位置而產生“軒然大波”，但其對于能量的貢獻較小。從圖中還可以看出隨著入射波浪頻率的變化，反射、透射系數有多個零點，即在某些頻率處，內界面上沒有內波模態的反射波或透射波。此外，自由水面上表面波模態的反射系數和透射系數變化趨勢(圖7(a))，當結構位于上層流體時，內界面上內波模態的反射系數和透射系數的變化趨勢則相同。

圖8(a)給出了內波模態波浪入射時，自由水面上表面波模態的反射和透射系數。由圖可知，當內波模態波浪入射時，入射波與結構物作用后，自由水面僅有非常微小的波動，所引起的波面升高基本可以忽略。圖8(b)給出了內波模態波浪入射時，內界面上內波模態波浪的反射和透射系數。由圖可知，由于本文所研究的結構物只位于上層流體，因此內界面上內波模態透射系數很大，接近于1，反射系數則很小，高頻時趨于0。

(a) 自由水面

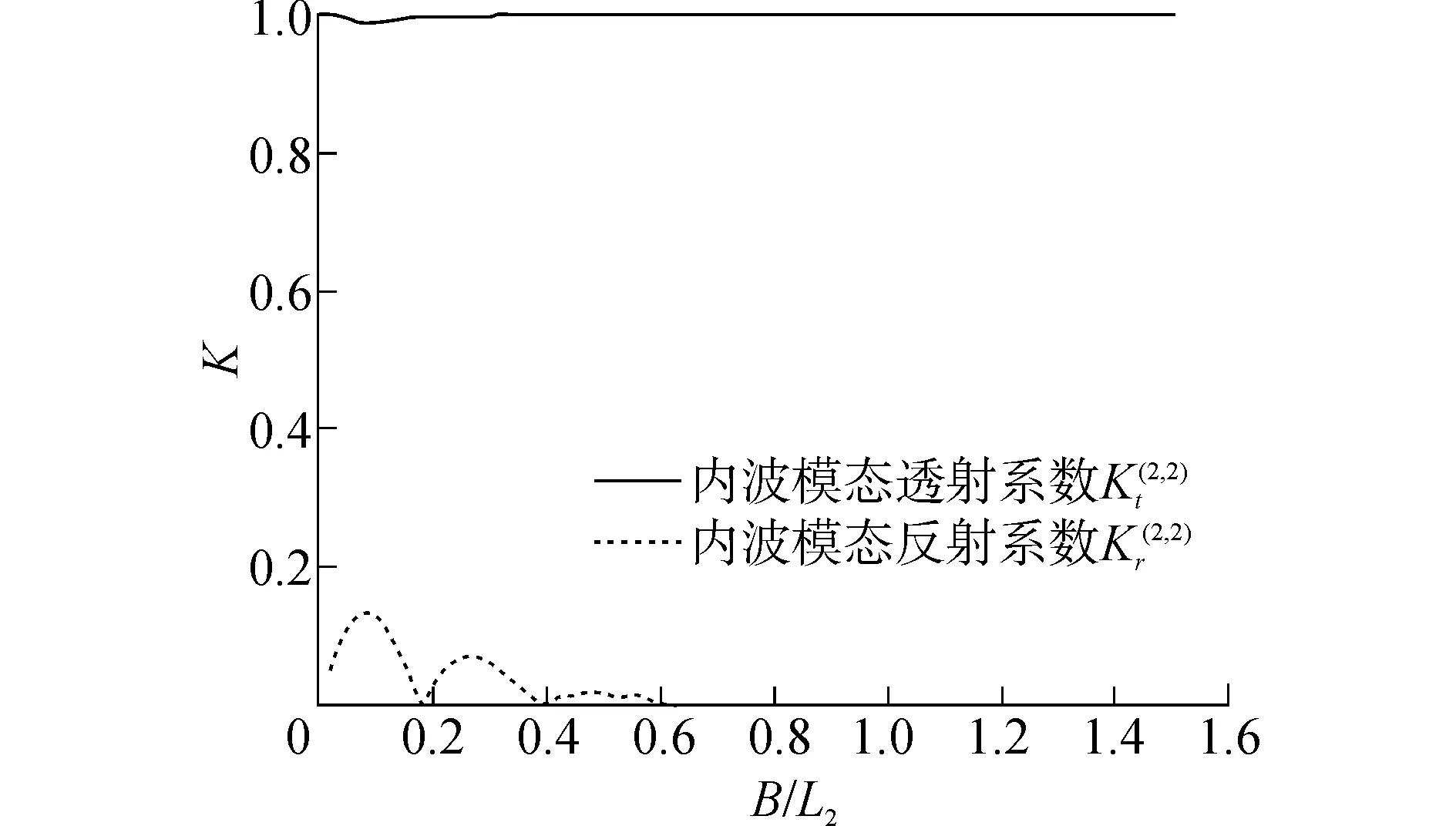
(b) 內界面圖8　入射波為內波模態時自由水面及內界面上的反射　和透射系數Fig.8　Reflection and transmission coefficients on free-surface and interface under incident internal-wave mode

根據圖7、8的結果可知，表面波模態入射時自由水面上表面波模態反透射特性與單層流體趨于一致；內波模態入射時自由水面上表面波模態反透射系數都很小接近于0，內界面上內波模態透射系數很大接近于1，反射系數則很小。因此下文僅研究表面波模態入射時，密度比、水深比及方箱寬度等參數的變化對內界面上內波模態反透射系數的影響規律。圖9為改變上下層密度比、入射波浪為表面波模態時，內界面上內波模態的反射和透射系數。由圖可以看出，隨著下層流體密度的增大，內界面反射和透射系數的最大值都減小，這是因為隨著密度差的增大，恢復力相應增大，內界面處抗擾動能力增強。同時，從結果中可以看出反射和透射系數零點的位置并不隨密度比的改變而改變，只與B/L2有關。反射系數零點出現在B/L2約為0.42、0.90和1.35的位置，透射系數零點出現在B/L2約為0.37、0.84和1.30的位置。

(a) 內界面反射系數

(b) 透射系數圖9　入射波為表面波模態時不同密度比下內界面　　反射和透射系數Fig.9　Reflection and transmission coefficients on interface 　with different density ration, under incident sur-　face-wave mode

(a) 反射系數

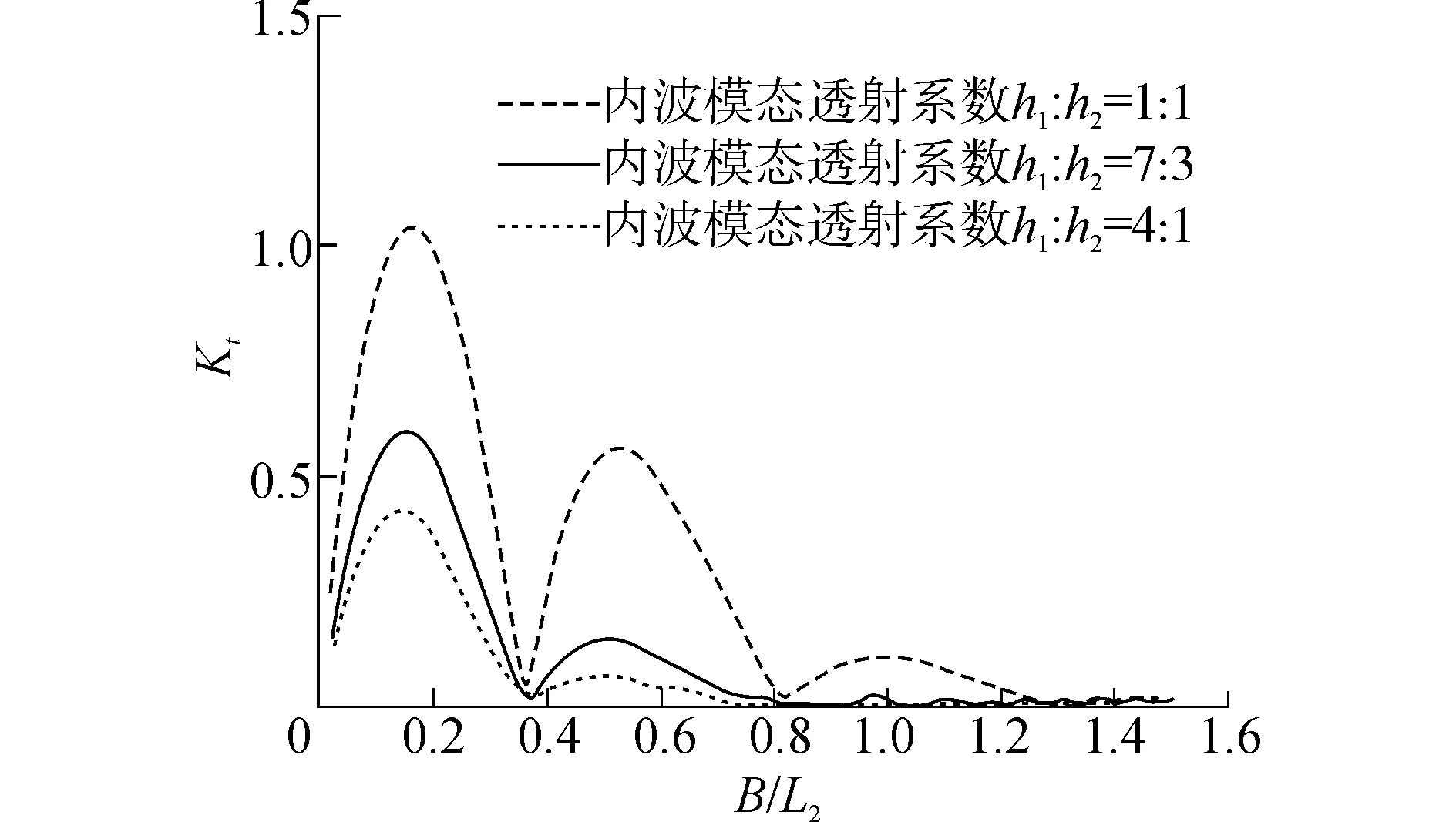
(b) 透射系數圖10　入射波為表面波模態時不同水深比下內界面反射　和透射系數Fig.10　Reflection and transmission coefficients on interface 　with different water depth ration, under incident 　surface-wave mode

圖10為改變上下層水深比、入射波浪為表面波模態時，內界面內波模態的反透射系數。由圖可知，結構物離內界面越近，則波浪入射后內界面的擾動越大，即反射和透射系數越大。內界面的位置同樣不影響反射和透射系數零點的位置。

圖11為改變方箱寬度、入射波為表面波模態時，內界面內波模態的反射和透射系數。由圖可知隨結構物寬度的增加，內界面內波模態的反射和透射系數在低頻時變化不大，高頻時明顯增大。但反射系數和透射系數的零點位置都幾乎不發生變化。

(a) 反射系數

(b) 透射系數圖11　入射波為表面波模態時不同方箱寬度下內界面反射　和透射系數Fig.11　Reflection and transmission coefficients on interface　with different box width, under incident surface-　wave mode

4結論

本文基于海洋密度層化的兩層流體簡化模型，基于線性勢流理論研究了兩層流體中箱型結構對波浪的反射和透射特性，得到結論如下：

1)無論入射波為何種模態，隨著入射頻率的變化，在某些頻率處內界面上的擾動為零，零點的位置只與B/L2的值相關，而與上下層密度比、水深比及箱體寬度沒有明顯關系。并且表面波模態波浪入射

時，內界面上內波模態波浪的反射和透射系數的變化趨勢基本相同；

2)內波模態入射波浪與結構物作用后，自由水面將產生非常微小的擾動；表面波模態入射波浪與結構物作用后，在內界面上則會產生大幅擾動，在高頻區域擾動趨于零。

參考文獻：

[1]方欣華, 杜濤. 海洋內波基礎和中國海內波[M]. 青島: 中國海洋大學出版社, 2005: 1-19.

[2]LAMB H. Hydrodynamics[M]. 6th ed. Cambridge: Cambridge University Press, 1993: 1-30.

[3]尤云祥, 繆國平, 程建生, 等. 兩層流體中水波在垂直薄板上的反射與透射[J]. 力學學報, 2005, 37(5): 529-541.

YOU Yunxiang, MIAO Guoping, CHENG Jiansheng, et al. Reflection and transmission of water waves past a vertical thin barrier in a two-layer fluid[J]. Chinese journal of theoretical and applied mechanics, 2005, 37(5): 529-541.

[4]DHILLON H, BANERJEA S, MANDAL B N. Wave scattering by a thin vertical barrier in a two-layer fluid[J]. International journal of engineering science, 2014, 78: 73-88.

[5]BEHERA H, SAHOO T. Gravity wave interaction with porous structures in two-layer fluid[J]. Journal of engineering mathematics, 2014, 87(1): 73-97.

[6]KASHIWAGI M, TEN I, YASUNAGA M. Hydrodynamics of a body floating in a two-layer fluid of finite depth. Part 2. diffraction problem and wave-induced motions[J]. Journal of marine science and technology, 2006, 11(3): 150-164.

[7]NGUYEN T C, YEUNG R W. Unsteady three-dimensional sources for a two-layer fluid of finite depth and their applications[J]. Journal of engineering mathematics, 2011, 70(1/2/3): 67-91.

[8]GOU Ying, CHEN Xinjia, TENG Bin. A time-domain boundary element method for wave diffraction in a two-layer fluid[J]. Journal of applied mathematics, 2012:686824.

[9]石強. 分層流體中浮式結構物水動力特性研究[D]. 上海: 上海交通大學, 2008: 55-89.

SHI Qiang. The study on hydrodynamic characteristics of floating structures in stratified fluids[D]. Shanghai: Shanghai Jiao Tong University, 2008: 55-89.

[10]石強, 尤云祥, 繆國平. 兩層流體中矩形箱浮體的附加質量和阻尼系數[J]. 海洋工程, 2007, 25(2): 33-42.

SHI Qiang, YOU Yunxiang, MIAO Guoping. Added mass and damping of a floating rectangular box in a two-layer fluid[J]. The ocean engineering, 2007, 25(2): 33-42.

[11]ZHANG Xinshu, BANDYK P. On two-dimensional moonpool resonance for twin bodies in a two-layer fluid[J]. Applied ocean research, 2013, 40: 1-13.

[12]李玉成, 滕斌. 波浪對海上建筑物的作用[M]. 北京: 海洋出版社, 2002: 12-74.

本文引用格式：

尚玉超，勾瑩，滕斌，等. 兩層流中二維箱體結構反射和透射的模擬研究[J]. 哈爾濱工程大學學報， 2016, 37(5): 653-659.

SHANG Yuchao, GOU Ying, TENG Bin， et al. Simulations of the reflection and transmission of water waves past box structures in a two-layer fluid[J]. Journal of Harbin Engineering University, 2016, 37(5): 653-659.

Simulations of the reflection and transmission of water waves past box structures in a two-layer fluid

SHANG Yuchao1, GOU Ying1, TENG Bin1,ZHENG Yanna2

(1. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024,China;2. Dalian Ocean University, Dalian 116023, China)

Abstract：Based on a simplified two-layer fluid model, the reflection and transmission characteristics of box structures were investigated in a two-layer fluid. In order to investigate the complex structures, a linearized frequency-domain model was developed by using a series expansion in the external domain and a higher-order boundary method in the internal domain. The continuity boundary condition was employed at the interface between the internal and external domains. In the internal domain, a Rankine source was used to avoid calculating a complex Green's function for the wave equation, and the velocity potentials on both the free surface and the internal surface were obtained directly. By comparison with the analytic results based on series expansion and verification of the energy-conservation principle, the proposed model was validated. By computing the reflection and transmission coefficients with the proposed model, the transformation between the two wave modes when the waves flow past box structures was analyzed and the reflection and transmission features were discussed.

Keywords：two-layer fluid; boundary element method; Rankine Source; reflection coefficient; transmission coefficient;water waves;box structures

收稿日期：2015-02-04.

基金項目：國家自然科學基金項目(51479026)；國家重點基礎研究發展計劃項目(2011CB013700-03); 中央高校基本科研業務費專項資金項目(DUT14ZD203).

作者簡介：尚玉超(1989-), 男,碩士研究生; 通信作者：勾瑩，E-mail:gouying@dlut.edu.cn.

DOI:10.11990/jheu.201502010

中圖分類號：O353.2

文獻標志碼：A

文章編號：1006-7043(2016)05-0653-07

網絡出版時間：2016-04-11.

勾瑩(1977-), 女,副教授,博士;

滕斌(1958-), 男,教授,博士生導師.