重視學生數學課堂教學中學習的延續性
黃美勤


【中圖分類號】G633.6 【文獻標識碼】A 【文章編號】2095-3089(2016)12-0045-02
每每在初一年級上學期期中考試后,在與學生家長的交流中,常常會聽到這樣的感嘆:“我的孩子在小學時,數學成績都是98分以上,怎么上了初中以后,數學成績越來越糟糕了呢?”而在與老師們的交流探討中,也有初中老師責怪小學老師知識教學不到位的現象。造成這樣的原因很多,但有一點值得引起我們的關注與重視,那就是要重視學生數學知識學習的延續性。何以學習的延續性?個人認為在學習前面相關的知識的過程中,不但要掌握和鞏固所學知識點,更要考慮能使學生應用所得到的知識去理解和學習后面的知識,為學習后續的知識做好鋪墊與準備,同時使學生學會正確的思維方法,分析題目中的數量關系,學會一把鑰匙開一把鎖,養成良好的學習習慣,以便不斷拓展學生知識視野。現在就自己的教學實踐,就數學課堂教學中學習的延續性談本人的一些體會。
二、舉一反三,融會貫通
21世紀數學課改要求培養學生應用數學的意識和解決問題的能力。這就是說,在教學的每一個環節中,要顧及學生思維活動的水平、思維的發展、概念的形成和理解教材的程度,根據所學知識采取符合學生心理特征的有效的課堂教學。這就說明數學教學活動的核心是數學思維活動,而數學思維活動就取決著思維延續性的拓展問題。說白了數學思維活動少不了解題中知識點的應用與其正確的思維方法的優化與組合。在初中數學中,學生應該掌握的數學思維無外乎對應、轉化、圖解、假設、替換等等,而這些數學思維不是單一存在的,比如以長方形這個知識來說,所涉及到的思路并不是某一節課或某一個問題的解決或某一道例題的思路就可以形成的,它們是有一個延續的循序漸進的過程逐步形成的,它是一個由量變到質變的過程。如在教學平移這個內容時,在知識的拓展應用中,我給出了這樣的題目:
(1)長方形綠地的長為32米,寬為20米,求綠地的面積。
(2)如圖1,在長為32米,寬為20米的長方形綠地中修兩條寬為2米的小路,求剩下綠地的面積。
(3)如圖1,在長為32米,寬為20米的長方形綠地中修兩條寬度相等的小路,并使剩下綠地的面積為540平方米,求小路的寬度。
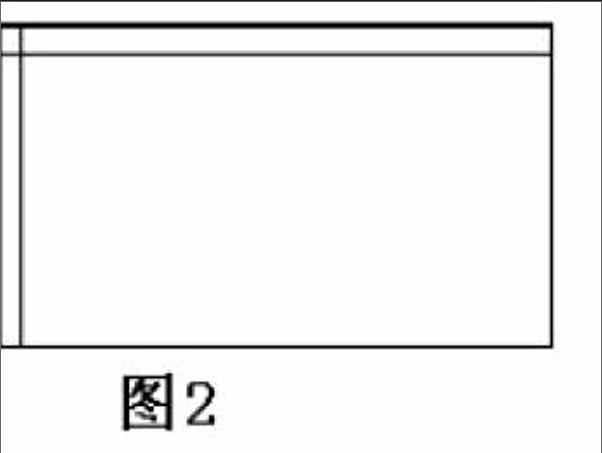
這三道題從數據到內容相差不大,解題的思維方法基本一致。但(1)題思維比較簡單,直接:長×寬=32×20=長方形面積,這是對小學知識的復習應用;(2)題的思維進了一步,要先將兩條小路分別向上、向左平移的如圖2。
此時綠地的面積依然是一個長方形,但長方形的長和寬已經發生了變化,通過平移之后,綠地的面積是長為30米,寬為18米的長方形的面積,才得出:長×寬=30×18=長方形綠地的面積,從而完成了小學知識到初一知識的延伸;(3)題的思維是一個上升,不但要將兩條小路分別向上、向左平移的如圖2,更要設小路的寬度為x米,此時綠地的面積雖然還是一個長方形,但長方形的長和寬已經不是單純的數字發生了變化,而是要知道通過平移之后,長和寬要知道用未知數來表示出來,在這里引導學生得出長方形的長是(32-x)米,寬是(20-x)米,這個過程是關鍵,最后得出:長×寬=(32-x)×(20-x)=長方形綠地的面積,即得出這樣一個方程(32-x)×(20-x)=540,在這個題目中,不但使思維靈活的學生得到了拓展,而且有意的滲透了用代數式表示長方形的長與寬,自然地把知識延伸到了數量關系可以用字母表示,對初三要涉及的一元二次方程的概念給予滲透,并且有意的告訴學生要解決這個方程還得學好初二的整式中的多項式乘以多項式這個計算內容。

