基于混沌加權一階局域法的IGS超快星歷鐘差預報

何成文　蔡成林

1　桂林電子科技大學信息與通信學院，桂林市金雞路1號，541004 2　廣西精密導航技術與應用重點實驗室，桂林市金雞路1號，541004

基于混沌加權一階局域法的IGS超快星歷鐘差預報

何成文1,2蔡成林1,2

1桂林電子科技大學信息與通信學院，桂林市金雞路1號，541004 2廣西精密導航技術與應用重點實驗室，桂林市金雞路1號，541004

摘要：為提高IGS超快星歷鐘差預報產品的精度，針對衛星鐘差數據具有確定項和隨機項成分的特點，在采用多項式模型對鐘差確定項建模的基礎上，提出采用混沌加權一階局域法對鐘差隨機項進行建模預報。仿真結果表明，采用混沌加權一階局域法的預報精度優于超快星歷鐘差預報產品。

關鍵詞：混沌；加權一階局域法；超快星歷；衛星鐘差；鐘差預報

提供高精度的實時鐘差產品是加速實時精密單點定位(precise point positioning，PPP)研究的重要途徑之一。由于提供鐘差數據的星載原子鐘一方面易受太空引力和衛星運行速度等外加環境因素的影響[1]，另一方面其自身頻率穩定性易受干擾，使得衛星實時鐘差數據呈現高度的非線性特點。因此，建立精確的實時鐘差預報模型非常困難。

盡管鐘差數據具有非線性且難以準確建模的特性，但在數據成分上，實時鐘差數據由確定項部分和隨機項部分組成。而IGS提供的超快星歷預報產品(IGU-P)正是基于鐘差的確定項部分來預報的[2]。因此，為了更大程度上提高IGU-P產品的預報精度，在對鐘差確定項進行建模預報的基礎上，提出采用混沌加權一階局域法對鐘差隨機項進行預報研究。

混沌理論是非線性科學的重要組成部分[3-4]，其主要包括3個參數：最大Lyapunov指數、時間延遲τ和嵌入維數m。最大Lyapunov指數表征時間序列的混沌特性，是混沌理論得以應用和推廣的首要條件；時間延遲τ表征混沌時間序列的最大可能不相關延遲階數；而嵌入維數m則表征一維混沌時間序列可以構建空間相點的維數，也可以表征序列提升空間維度的大小。混沌理論利用這3個參數不僅可以將雜亂無序的一維隨機時間序列按照時間延遲τ和嵌入維數m進行重新采樣，從而構造出一個多維的有序時間序列，還可以解決一維非線性隨機序列的高精度預報問題。加權一階局域法是混沌理論中一種預報精度較高的方法，其以預報點時間上最近的相點為中心點，通過尋找空間上離中心點最近的相點來構建線性模型進行預報。該模型與自回歸移動平均模型相比，具有預報長度不受模型階數限制的優點，在時間序列預報研究方面取得了較好的效果[3-4]。

1鐘差數據確定項的多項式模型

鐘差數據確定項又稱為鐘差的物理特性[2]，其常規模型表達式為：

(1)

式中，clk(t)為鐘差原始數據；W(t)為鐘差趨勢項成分，其表達式為：

(2)

式中，A、B、C分別對應鐘差的相位、頻率和頻漂參數[1-2]。通過對鐘差相位數據作二次單步差分運算，然后依據殘差序列的最小二乘擬合直線的斜率值大小來判決C值是否為0。若C為0，則對clk(t)采用最小二乘直線擬合方式計算A和B的參數值；若C不為0，則采用式(2)進行最小二乘曲線擬合，得到A、B和C3個參數值。

式(1)中，S(t)為鐘差周期項成分，其與W(t)一起構成鐘差確定項部分，其表達式為：

(3)

利用式(3)，對去除鐘差趨勢項成分的殘差數據，利用頻譜分析技術確定N的最大取值和ωi的各個取值，然后通過最小二乘周期擬合法求出相應周期的振幅和相位參數。

式(1)中ψ(t)為鐘差隨機項部分，其為本文混沌加權一階局域法重點研究的內容。

2鐘差數據隨機項的混沌加權一階局域法模型

假設衛星鐘差隨機項時間序列為xi(i=1,2,…，N)，其最大Lyapunov指數為正，其時間延遲階數和嵌入維數參數分別為τ和m，則重構相空間后的相點Yj=[xj,xj+τ,xj+2τ,…,xj+(m-1)τ]，其中j=1,2,…,N-(m-1)τ。

若中心點Yk的鄰近相點為Yki(i=1,2,…,q)，其中q值人為設置，并且Yki到Yk的距離記為di，記dm為di中的相對最小值，則Yki的權值為：

(4)

式中，a取值為1，與下文的a意義不同。

混沌加權一階局域法預測模型為：

(5)

式中，e為1行m列單位陣，運用加權最小二乘法原理計算其系數：

(6)

由式(6)計算出a、b的值后，運用式(5)依次更新中心點，從而達到迭代預報的目的。

3基于混沌加權一階局域法的IGS鐘差預報

3.1鐘差預報建模流程

基于混沌加權一階局域法進行IGS超快星歷鐘差預報的流程如下：

1)對IGU-O產品的鐘差原始數據進行鐘跳檢測與修復；

2)對IGU-O產品的鐘差數據進行粗差探測和修復；

3)對鐘跳檢測和粗差探測后的鐘差數據進行二次單步差分處理，以確定鐘差數據的趨勢項成分階數；

4)對去除趨勢項成分的鐘差數據作頻譜分析，得出其顯著周期項，最后得到去除趨勢項和周期項的隨機項殘差數據；

5)對上一步得到的隨機項殘差數據進行濾波去噪處理，得到較為干凈的鐘差隨機項殘差數據；

6)對濾波去噪后的隨機項時間序列分別采用互信息法和Cao方法計算其時間延遲階數和嵌入維數參數，以及采用小數據量法判斷最大Lyapunov指數的正負性[5-7];

7)依據上一步計算出來的3個混沌參數，采用加權一階局域法對隨機項殘差序列進行建模預報；

8)將上一步的預報數據和對應時刻的IGU-P產品數據分別與第2天對應時刻的IGU產品的IGU-O觀測部分作差，以均方誤差作為精度評價指標，進而得出兩者的預報精度。

上述步驟中，前2個步驟為數據預處理過程，中間3個步驟為確定項建模過程，后面3個步驟為隨機項建模預報部分。

3.2算例分析

為了充分驗證混沌加權一階局域法對實時鐘差預報精度具有改善作用，超快星歷鐘差數據從IGS網站ftp:∥cddis.gsfc.nasa.gov下載，數據采樣頻率為15min，數據采集時段為2011-10-29～11-12。另外，各顆衛星服務時間與星載原子鐘類型信息可從http:∥gge.unb.ca/Resources/GPSConstellationStatus.txt網址獲取。

從上述15d數據文件中任取1d的IGU產品作為建模數據，運用1d的IGU-O觀測數據測試各顆衛星的趨勢項階數、顯著周期項、最大Lyapunov指數、時間延遲階數和嵌入維數5個參數，測試結果見表1。為節省篇幅，在充分考慮星載原子鐘類型和服務時間的前提下，選用PRN04、PRN19、PRN31和PRN25衛星進行分析。同時以被選取IGU產品的下一個IGU產品的IGU-O觀測部分數據作為被選取IGU產品的IGU-P預報部分的真值，兩種方法的實時鐘差預報效果如圖1所示。

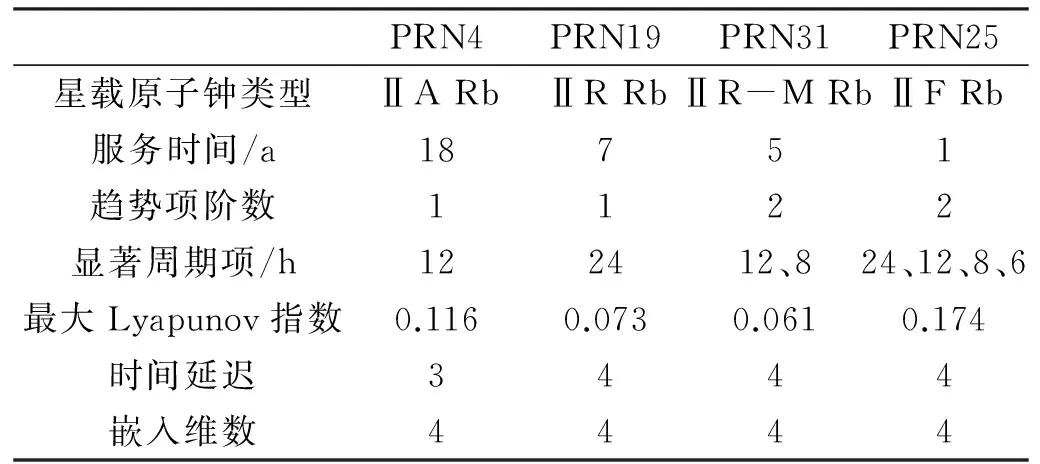
表1　衛星參數統計

從表1可見：

1)前2顆衛星趨勢項階數為1，后2顆衛星趨勢項階數為2，這主要與星載原子鐘提供服務的時間長短有關。在一定程度上說明，星載原子鐘服務時間越長，鐘差相位數據線性性越好。星載原子鐘服務初期，鐘差數據的頻漂值較大。

2)各顆衛星的顯著周期項最多為4個，至少有1個，說明鐘差數據內部具有顯著周期性，間接論證了IGS采用確定項預報IGU-P產品數據的可行性。

3)各顆衛星的最大Lyapunov指數均為正數，說明鐘差隨機項殘差序列具有混沌特性。

4)各顆衛星的時間延遲階數和嵌入維數相對一致，說明星載原子鐘數據的非線性特性具有內部一致性。

圖1　衛星PRN04、PRN19、PRN31、PRN25的超快星歷鐘差及其預報效果Fig.1　Ultra-rapid ephemeris clock error and prediction error of the PRN04、PRN19、PRN31、PRN25 satellites

從圖1可以看出，在建模1 d的預報效果中，采用本文方法對鐘差預報的效果明顯優于IGU-P產品。提升幅度從0.2 ns到2 ns不等，直接驗證了單天內本文方法對實時鐘差預報具有一定的改進功能，且效果較好。

為了更好地說明本文方法比IGU-P預報的精度高，將表1中的5個參數保持不變(即固定預測模型)，將測試數據集從1 d擴大到14 d。測試方案以前14 d的IGU-O觀測數據作為建模數據，以后14 d的IGU-O觀測數據作為對應前14 d IGU-P預報數據的真值，依次迭代預報。利用均方誤差作為精度評價指標，采用統計平均法測試得到14 d內PRN04、PRN19、PRN31和PRN25四顆衛星在3 h、6 h、12 h、24 h時間段內2種預報方法的精度，預報效果如表2(A為IGU-P，B為本文方法，單位為ns)所示。

表2　14 d預報精度對比統計表

結合表1和表2的數據得出：

1)在3 h、6 h、12 h和24 h時間段內，采用本文方法的4顆衛星鐘差預報精度均優于IGU-P產品，且平均提升幅度分別為16%、10%、13.5%和26.3%，改進效果顯著。

2)不同的星載原子鐘類型在短期IGU超快星歷預報中差異并不明顯。

3)PRN25號衛星星載原子鐘的服務時間為1 a，相對于其他原子鐘，IGS單天預報均方誤差相對較高，但是采用本文提出的混沌加權一階局域法的預報精度大幅提高。

4結語

1)確定衛星鐘差數據的趨勢項階數、顯著周期項、最大Lyapunov指數、時間延遲階數和嵌入維數5個參數是本文方法提高預報精度的基礎。

2)星載原子鐘的服務時間對預報性能有較大影響，服務時間越長，預報性能越好。

3)本文方法的預報精度明顯優于IGU-P產品，為實時PPP推廣提供了理論依據。

另外，本文方法驗證的數據集最大為14 d，相對于目前GPS星載原子鐘的實際服務時間(20 a)較短。因而，本文方法提出的5個星載原子鐘參數隨著時間的增長是否會發生明顯改變及如何變化，將是下一步需要研究的內容。

致謝:對長安大學黃觀文老師提供的幫助表示感謝！

參考文獻

[1]郭海榮.導航衛星原子鐘時頻特性分析理論與方法研究[D].鄭州：信息工程大學，2006(Guo Hairong.Stydy on the Analysis Theories and Algorithms of the Time and Frequency Characterization for Atomic Clocks of Navigation Satellites[D].Zhengzhou:Information Engineering University,2007)

[2]黃觀文.GNSS星載原子鐘質量評價及精密鐘差算法研究[D].西安：長安大學，2012(Huang Guanwen.Research on Algorithms of Precise Clock Offset and Quality Evaluation of GNSS Satellite Clock[D].Xi’an:Chang’an University,2012)

[3]呂金虎.混沌時間序列分析及其應用[M].武漢：武漢大學出版社，2002(Lv Jinhu.The Analysis and Application of Chaotic Time Series[M].Wuhan:Wuhan University Press,2002)[4]韓敏.混沌時間序列預測理論與方法[M].北京：中國水利水電出版社，2007(Han Min.The Prediction Theory and Method of Chaotic Time Series[M].Beijing: China Water Conservancy and Hydropower Press,2007)

[5]Rosenstein M T, Collins J J, Deluca C J. A Practical Method for Calculating Largest Lyapunov Exponents from Small Data Sets[J].Physica D:Nonlineax Phenom,1993,65:117-134

[6]Fraser A M, Swinney H L. Independent Coordinates for Strange Attractors from Mutual Information[J].Phys Rev A,1986,33:1 134-1 140

[7]Kim H S, Eykholt R, Salas J D. Nonlinear Dynamics, Delay Times, and Embedding Windows[J].Phys D: Nonlinear Phenom, 1999,27(1):48-60

Foundation support:National Natural Science Foundation of China,No.61263028;Innovation Project of GUET Graduate Education,No.YJCXS201530.

About the first author:HE Chengwen, postgraduate, majors in GNSS time transmission and precise orbit determination, E-mail:cwhe_10@163.com.

Prediction of IGS Ultra-Rapid Ephemeris Clock Error Based on Adding-Weight One-Rank Local-Region Method of Chaos

HEChengwen1,2CAIChenglin1,2

1School of Information and Communication,Guilin University of Electronic Technology, 1 Jinji Road, Guilin 541004,China 2Guangxi Key Laboratory of Precision Navigation Technology and Application, 1 Jinji Road, Guilin 541004,China

Abstract:In order to improve the accuracy of IGS ultra-rapid predicted products(IGU-P), in response to the data characteristic of ultra-rapid ephemeris composed of both determined and random items, a new prediction algorithm is proposed. This proposed algorithm is based on a polynomial model, which models random items with adding-weight one-rank local-region method of chaos. The results from the calculating examples show that the accuracy of adding-weight one-rank local-region method of chaos is superior to that of the IGU-P.

Key words:chaos；adding-weight one-rank local-region method；ultra-rapid ephemeris；satellite clock error；clock error prediction

收稿日期：2015-08-03

第一作者簡介：何成文，碩士生，主要從事GNSS時間傳遞和精密定軌研究,E-mail: cwhe_10@163.com。

DOI：10.14075/j.jgg.2016.07.004

文章編號：1671-5942(2016)07-0577-04

中圖分類號：P228

文獻標識碼：A

項目來源：國家自然科學基金(61263028)；桂林電子科技大學研究生教育創新計劃(YJCXS201530)。