優(yōu)化的長(zhǎng)山水道船舶交通流量灰色系統(tǒng)預(yù)測(cè)模型

馬曉波+劉雪菲+戴冉

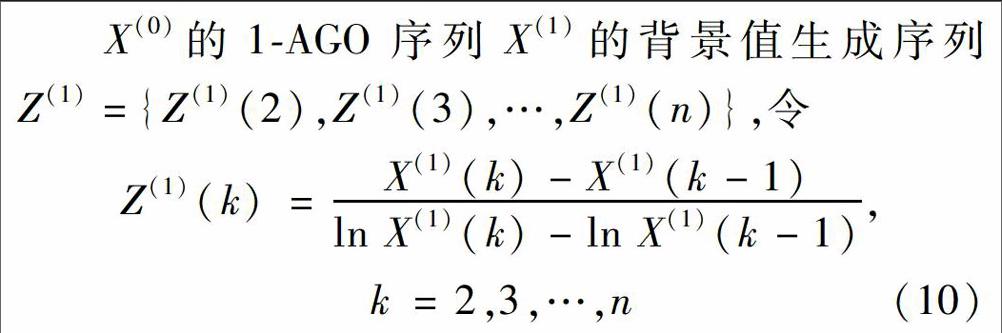
摘要：

為提高長(zhǎng)山水道船舶交通流量的預(yù)測(cè)精度，對(duì)灰色系統(tǒng)中的GM（1，1）模型進(jìn)行優(yōu)化.在對(duì)長(zhǎng)山水道船舶交通流量進(jìn)行分析的基礎(chǔ)上，通過改進(jìn)GM（1，1）模型背景值、改變初始條件、增加新信息優(yōu)先權(quán)、引入殘差修正等方法對(duì)GM（1，1）模型進(jìn)行優(yōu)化.通過該優(yōu)化模型的預(yù)測(cè)數(shù)據(jù)與歷史數(shù)據(jù)的比較驗(yàn)證了該優(yōu)化模型的準(zhǔn)確性和可靠性.最后用該優(yōu)化模型對(duì)長(zhǎng)山水道2015—2016年的船舶交通流量進(jìn)行了預(yù)測(cè).

關(guān)鍵詞：

水路運(yùn)輸；船舶交通流量；灰色預(yù)測(cè)；GM（1，1）優(yōu)化模型

中圖分類號(hào)：U691

文獻(xiàn)標(biāo)志碼：A 收稿日期：20151011 修回日期：20151130

0引言

長(zhǎng)山水道地處黃海與渤海交匯處，是船舶進(jìn)出天津港、秦皇島港、黃驊港、濰坊港、東營(yíng)港、龍口港、萊州港、蓬萊港等各港口的重要水上通道之一.隨著環(huán)渤海各港口吞吐量的日益增加，長(zhǎng)山水道船舶交通流量也迅猛增長(zhǎng).

船舶交通流量預(yù)測(cè)為航道的規(guī)劃、設(shè)計(jì)和船舶通航管理提供基礎(chǔ)性依據(jù).[1]船舶交通流量的準(zhǔn)確預(yù)測(cè)有助于提高海事管理的效能[2]，為海事管理部門的科學(xué)決策提供有力支持.

常用的交通流量的定量預(yù)測(cè)方法主要有時(shí)間序列法、回歸分析法、灰色預(yù)測(cè)模型法、神經(jīng)網(wǎng)絡(luò)法、模糊預(yù)測(cè)法等.近幾年也出現(xiàn)了一些新的方法：組合預(yù)測(cè)法、遺傳基因預(yù)測(cè)法、多因素組合分析法、支持向量機(jī)法等.[36]灰色預(yù)測(cè)模型所需數(shù)據(jù)量較少，計(jì)算方法簡(jiǎn)單，不需要太多的關(guān)聯(lián)因素，可用于短、中、長(zhǎng)期預(yù)測(cè).[78]與線性回歸預(yù)測(cè)模型相比，灰色預(yù)測(cè)模型的優(yōu)點(diǎn)是可以處理非線性問題；與模糊預(yù)測(cè)模型相比，灰色預(yù)測(cè)模型的優(yōu)點(diǎn)是可以隨時(shí)對(duì)模型進(jìn)行修正以提高預(yù)測(cè)精度.[9]因此，灰色預(yù)測(cè)模型對(duì)于長(zhǎng)山水道船舶交通流量的預(yù)測(cè)具有良好的適用性.已有多位學(xué)者通過改進(jìn)GM（1，1）模型背景值[1011]、改變模型初始條件、增加新信息優(yōu)先權(quán)[10，12]、引入殘差修正等方法[10]建立了優(yōu)化的灰色預(yù)測(cè)模型，并將模型應(yīng)用于經(jīng)濟(jì)、管理、工程方面.本文通過將上述優(yōu)化后的模型應(yīng)用于長(zhǎng)山水道的船舶交通流量的預(yù)測(cè)中，證明優(yōu)化后的灰色預(yù)測(cè)模型在船舶交通流量預(yù)測(cè)的研究中同樣具有較高的精度和實(shí)用價(jià)值.

1傳統(tǒng)的GM（1，1）模型

設(shè)原始序列為X（0）={X（0）（1），X（0）（2），…，X（0）（n）}，則X（0）的1AGO序列為X（1）={X（1）（1），X（1）（2），…，X（1）（n）}，其中

將原始數(shù)據(jù)累加會(huì)弱化原始數(shù)據(jù)的隨機(jī)性.若序列X（0）和序列X（1）滿足準(zhǔn)光滑性檢驗(yàn)、準(zhǔn)指數(shù)規(guī)律檢驗(yàn)和級(jí)比檢驗(yàn)，則符合灰色預(yù)測(cè)的前提，其灰色微分方程為

2GM（1，1）模型的優(yōu)化

為使GM（1，1）模型更加客觀合理地預(yù)測(cè)長(zhǎng)山水道船舶交通流量，結(jié)合長(zhǎng)山水道的歷史背景和發(fā)展現(xiàn)狀，對(duì)模型進(jìn)行優(yōu)化.

2.1背景值的優(yōu)化

隨著環(huán)渤海經(jīng)濟(jì)圈的迅猛發(fā)展，進(jìn)出渤海灣的船舶交通流量劇增，長(zhǎng)山水道船舶交通流量也迅猛增長(zhǎng)，船舶通航密度越來越大.長(zhǎng)山水道1998年的船舶交通流量為6454艘次（日均17.7艘次）[13]，2014年為52524艘次（日均143.9艘次），數(shù)據(jù)來源于山東海事局；年平均增長(zhǎng)速率為44.61%.因此，結(jié)合長(zhǎng)山水道船舶交通流量增速快的特點(diǎn)，對(duì)GM（1，1）模型的背景值進(jìn)行優(yōu)化.

X（0）的1AGO序列X（1）的背景值生成序列Z（1）={Z（1）（2），Z（1）（3），…，Z（1）（n）}，令

優(yōu)化背景值后，模型適用于各種發(fā)展系數(shù)的情形，即使在發(fā)展系數(shù)較大時(shí)模型也可用于中長(zhǎng)期預(yù)測(cè)，并且預(yù)測(cè)精度較高[11].

2.2增加新信息優(yōu)先權(quán)

長(zhǎng)山水道船舶交通流量受國(guó)家政策影響較大.隨著環(huán)渤海沿岸各港口泊位的不斷開發(fā)，各港口吞吐量穩(wěn)定增長(zhǎng)，抵港船舶的數(shù)量不斷增加.綜合上述事實(shí)，同時(shí)考慮水文、氣象等影響船舶航行的要素在一定時(shí)期內(nèi)變化的連續(xù)性，賦予與預(yù)測(cè)時(shí)間較接近時(shí)期的信息較大的權(quán)重，以提高灰色建模的功效.本文將X（1）（n）作為灰色微分模型的初始條件.對(duì)式（8）的求導(dǎo)還原得

越新的數(shù)據(jù)對(duì)預(yù)測(cè)值的影響越大，通過賦予新信息較大的權(quán)重可以使新信息得到充分利用，提高模型的預(yù)測(cè)精度.

2.3殘差修正

人為因素是影響船舶交通流量的重要因素.由于老鐵山水道和長(zhǎng)山水道均可通往天津港、秦皇島港、黃驊港等港口，為減小人為因素對(duì)船舶航線選擇的影響，提高預(yù)測(cè)精度，對(duì)經(jīng)過上述改進(jìn)后的GM（1，1）模型進(jìn)行殘差修正.對(duì)X（1）={X（1）（1），X（1）（2），…，X（1）（n）}，有預(yù)測(cè)序列X^（1）={X^（1）（1），X^（1）（2），…，X^（1）（n）}，定義殘差為

經(jīng)檢驗(yàn)，表1中數(shù)據(jù)可作為GM（1，1）建模數(shù)據(jù)且能進(jìn)行數(shù)據(jù)灰色預(yù)測(cè).將優(yōu)化后的GM（1，1）模型用于長(zhǎng)山水道船舶交通流量的預(yù)測(cè)，利用MATLAB軟件對(duì)傳統(tǒng)的GM（1，1）模型和優(yōu)化后的GM（1，1）模型進(jìn)行編程求解并分析預(yù)測(cè)結(jié)果.

由于越新的數(shù)據(jù)對(duì)預(yù)測(cè)值的影響越大，本文將2014年的船舶交通流量作為灰色微分模型的初始條件，此時(shí)n取常數(shù)10，得到的預(yù)測(cè)公式為

從表2和3可以看出，傳統(tǒng)的GM（1，1）模型的預(yù)測(cè)誤差率的最大值為21.24%，而優(yōu)化后的GM（1，1）模型的預(yù)測(cè)誤差率的最大值為9.17%.此外，優(yōu)化后的GM（1，1）模型的預(yù)測(cè)平均誤差率僅為3.44%，較傳統(tǒng)的GM（1，1）模型提高了近5%.同時(shí)，由表3可知，傳統(tǒng)的GM（1，1）模型預(yù)測(cè)的平均誤差為3241.8艘次，優(yōu)化后的GM（1，1）模型預(yù)測(cè)的平均誤差為1330.9艘次，優(yōu)化模型的預(yù)測(cè)誤差約為傳統(tǒng)模型預(yù)測(cè)誤差的1/3.優(yōu)化后的GM（1，1）模型的關(guān)聯(lián)度也有所提高.

從圖1可以看出，優(yōu)化模型預(yù)測(cè)曲線更加符合原始數(shù)據(jù)曲線的變化趨勢(shì).優(yōu)化模型能夠有效地減少原始數(shù)據(jù)的波動(dòng)性所帶來的預(yù)測(cè)誤差.因此，相對(duì)于傳統(tǒng)模型的預(yù)測(cè)值曲線，優(yōu)化模型的預(yù)測(cè)曲線能夠更好地?cái)M合實(shí)際值曲線，擬合效果理想，預(yù)測(cè)結(jié)果可信.

表4和5分別為灰色預(yù)測(cè)模型的精度評(píng)判標(biāo)準(zhǔn)和模型精度檢驗(yàn)值的比較，其中p為小誤差概率，C為方差比.

由表4和5可知，傳統(tǒng)的GM（1，1）模型的精度等級(jí)和優(yōu)化后的GM（1，1）模型的精度等級(jí)均為1級(jí)（好）.這說明GM（1，1）模型本身適用于長(zhǎng)山水道船舶交通流量的預(yù)測(cè).優(yōu)化模型的方差比比傳統(tǒng)模型的更小（見表5），說明優(yōu)化模型的預(yù)測(cè)精度更高.

綜上所述，優(yōu)化后的GM（1，1）模型的數(shù)據(jù)誤差較小，預(yù)測(cè)精度高，預(yù)測(cè)結(jié)果更能反映實(shí)際的船舶交通流量發(fā)展趨勢(shì)和規(guī)律.優(yōu)化后的GM（1，1）模型更適用于對(duì)隨機(jī)性、不確定性較強(qiáng)的航道船舶交通流量進(jìn)行預(yù)測(cè).

利用上述預(yù)測(cè)公式對(duì)2015和2016年長(zhǎng)山水道的船舶交通流量進(jìn)行預(yù)測(cè).將2015和2016年的k值分別取11和12，代入公式得2015年和2016年的船舶交通流量分別為56188艘次和59927艘次.

4總結(jié)與展望

優(yōu)化后的GM（1，1）模型融合了3種算法的優(yōu)勢(shì)：通過優(yōu)化背景值，使模型適用于各種發(fā)展系數(shù)的情形，即使在發(fā)展系數(shù)較大時(shí)也可用于中長(zhǎng)期預(yù)測(cè)，并且預(yù)測(cè)精度較高；通過賦予新信息較大的權(quán)重，使新信息得到充分利用，有助于提高模型的預(yù)測(cè)精度；可通過殘差優(yōu)化，減小人為因素對(duì)船舶航線選擇的影響.

優(yōu)化后的GM（1，1）模型對(duì)長(zhǎng)山水道船舶交通流量的預(yù)測(cè)平均相對(duì)誤差率僅為3.44%，說明該優(yōu)化模型具有較高的實(shí)際應(yīng)用和參考價(jià)值.

該優(yōu)化模型充分考慮到了船舶流量的發(fā)展變化，港口泊位的不斷發(fā)展，港口吞吐量的變化，水文、氣象等影響船舶航行的要素及人為因素，對(duì)樣本數(shù)據(jù)較少、發(fā)展較快、受政策影響較大的港口及航道的船舶交通流量預(yù)測(cè)具有良好的適用性.

本文中的優(yōu)化模型，在預(yù)測(cè)精度方面較傳統(tǒng)的GM（1，1）模型有明顯提高.但若原始數(shù)據(jù)序列的光滑度較差，則該優(yōu)化模型的精度有待進(jìn)一步提高.為提高該優(yōu)化模型的準(zhǔn)確性和廣泛適用性，可嘗試?yán)煤瘮?shù)f（x（0）（k））=（x（0）（k）+1）1p（p<0）提高原始數(shù)據(jù)序列x（0）（k）的光滑度.該方法的有效性已經(jīng)得到理論證明[14].同時(shí)，由于模型背景值與灰度值相互作用，可能影響預(yù)測(cè)精度，可以通過判別序列x（1）（k）的凹凸性，使灰度值與背景值在不同的發(fā)展系數(shù)下相互協(xié)調(diào)，從而加以探究[10].

準(zhǔn)確的船舶交通流量預(yù)測(cè)能為港口管理部門的控制決策提供可靠的數(shù)據(jù)依據(jù)，為疏通道路、減少海上事故、合理配置交通資源提供極大的幫助.在實(shí)際應(yīng)用中，可根據(jù)原始數(shù)據(jù)，建立實(shí)時(shí)模型，并不斷對(duì)模型進(jìn)行更新，實(shí)現(xiàn)較為準(zhǔn)確的預(yù)測(cè).

參考文獻(xiàn)：

[1]劉敬賢，張濤，劉文.船舶交通流組合預(yù)測(cè)方法研究[J].中國(guó)航海，2009，32（3）：8084.

[2]翟久剛，田延飛，嚴(yán)新平.基于BP神經(jīng)網(wǎng)絡(luò)與殘差分析的船舶交通流量預(yù)測(cè)[J].上海海事大學(xué)學(xué)報(bào)，2013，34（1）：1922.

[3]李俊，徐志京，唐貝貝.基于GA優(yōu)化的灰色神經(jīng)網(wǎng)絡(luò)船舶交通流量預(yù)測(cè)方法研究[J].船海工程，2013，42（5）：135137.

[4]鄭友銀，徐志京.基于灰色自回歸模型的船舶流量預(yù)測(cè)方法[J].船海工程，2011，40（1）：122124.

[5]馮宏祥，肖英杰，孔凡邨.基于支持向量機(jī)的船舶交通流量預(yù)測(cè)模型[J].中國(guó)航海，2011，34（4）：6268.

[6]李紅喜，付玉慧，張仁初.港口船舶交通流量預(yù)測(cè)[J].大連海事大學(xué)學(xué)報(bào)，2009，35（3）：4042.

[7]鄭剛.基于灰色模型的集裝箱貨量預(yù)測(cè)[J].中國(guó)航海，2014，37（2）：118121.

[8]張樹奎，肖英杰.船舶交通流量預(yù)測(cè)的灰色神經(jīng)網(wǎng)絡(luò)模型[J].上海海事大學(xué)學(xué)報(bào)，2015，36（1）：4649.

[9]谷川，張?jiān)?GM（1，1）灰色模型改進(jìn)及其應(yīng)用[J].海洋測(cè)繪，2008，28（3）：3537.

[10]尚軍亮，方敏.一種優(yōu)化的高精度灰色GM（1，1）預(yù)測(cè)模型[J].電子與信息學(xué)報(bào)，2010，32（6）：13011305.

[11]羅黨，劉思峰，黨耀國(guó).灰色模型GM（1，1）優(yōu)化[J].中國(guó)工程科學(xué)，2003，15（18）：5054.

[12]黨耀國(guó)，劉思峰，劉斌.以x（1）（n）為初始條件的GM模型[J].中國(guó)管理科學(xué)，2005，13（1）：132135.

[13]張興軍，于濤.長(zhǎng)山水道交通現(xiàn)狀分析及海事監(jiān)管對(duì)策[J].水運(yùn)科學(xué)研究，2009（1）：3438.

[14]彭勇，陳俞強(qiáng).一種改進(jìn)的灰度預(yù)測(cè)模型[J].計(jì)算機(jī)與數(shù)字工程，2012，40（1）：4041.