計算機輔助教學對數學創(chuàng)造性思維的影響研究

王華

[摘 要] 計算機輔助教學（CAI）在高中數學課堂中得到了廣泛的應用，那么如何讓它更有利于發(fā)展學生的創(chuàng)造性思維，構建計算機輔助教學特有的教學模式，本文采用等組折中控制前后測實驗法對高一學生進行了實驗研究，從計算機輔助教學的幾個特性分析了實驗結果，得到了一些反思.

[關鍵詞] 計算機輔助教學；創(chuàng)造性思維；實驗研究

在高中數學新課程標準推廣的近幾年，計算機輔助教學（CAI）已在各校的高中數學課堂中廣泛的應用，它打破了原有的粉筆加黑板的傳統(tǒng)數學教學方式，引起了課堂內容的變革. 但計算機輔助教學除了改革高中數學課堂的教學模式，它對高中學生的數學創(chuàng)造性思維是否有影響，是否有利于學生創(chuàng)造性思維的發(fā)展以及在教學實驗的實踐中不斷積累計算機輔助教學的教學資料，逐步構建計算機輔助教學的教學模式，為其在校內乃至更大的范圍的推廣積累經驗. 帶著這兩個目的，筆者對2014屆高一新生進行了調查研究.

前期準備

本課題的研究方法為實驗法.實驗假設為計算機輔助教學有助于高一學生創(chuàng)造性思維的發(fā)展. 實驗設計采用等組折中控制前后測實驗法. 實驗對象為14屆高一新生，將其隨機分派編班后，隨機抽出兩個班，其一為實驗班（高一1班），其二為控制班（高一7班）. 實驗因子為計算機輔助數學教學. 本實驗的測量工具采用自編的數學創(chuàng)造性思維檢測題.

本課題研究的理論基礎——建構主義學習理論及創(chuàng)造性思維培養(yǎng)理論，結合高中生的學習心理特點，初步構建了計算機輔助數學教學以培養(yǎng)學生創(chuàng)造性思維的教學模式.

操作過程

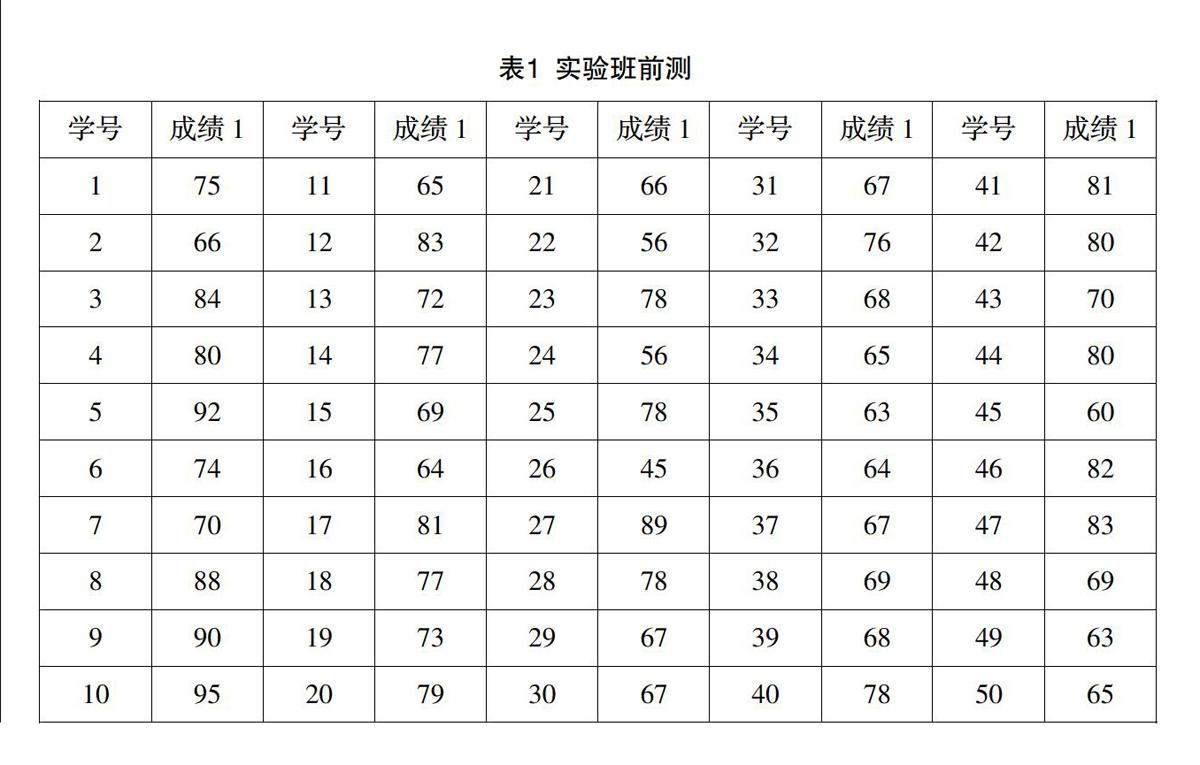
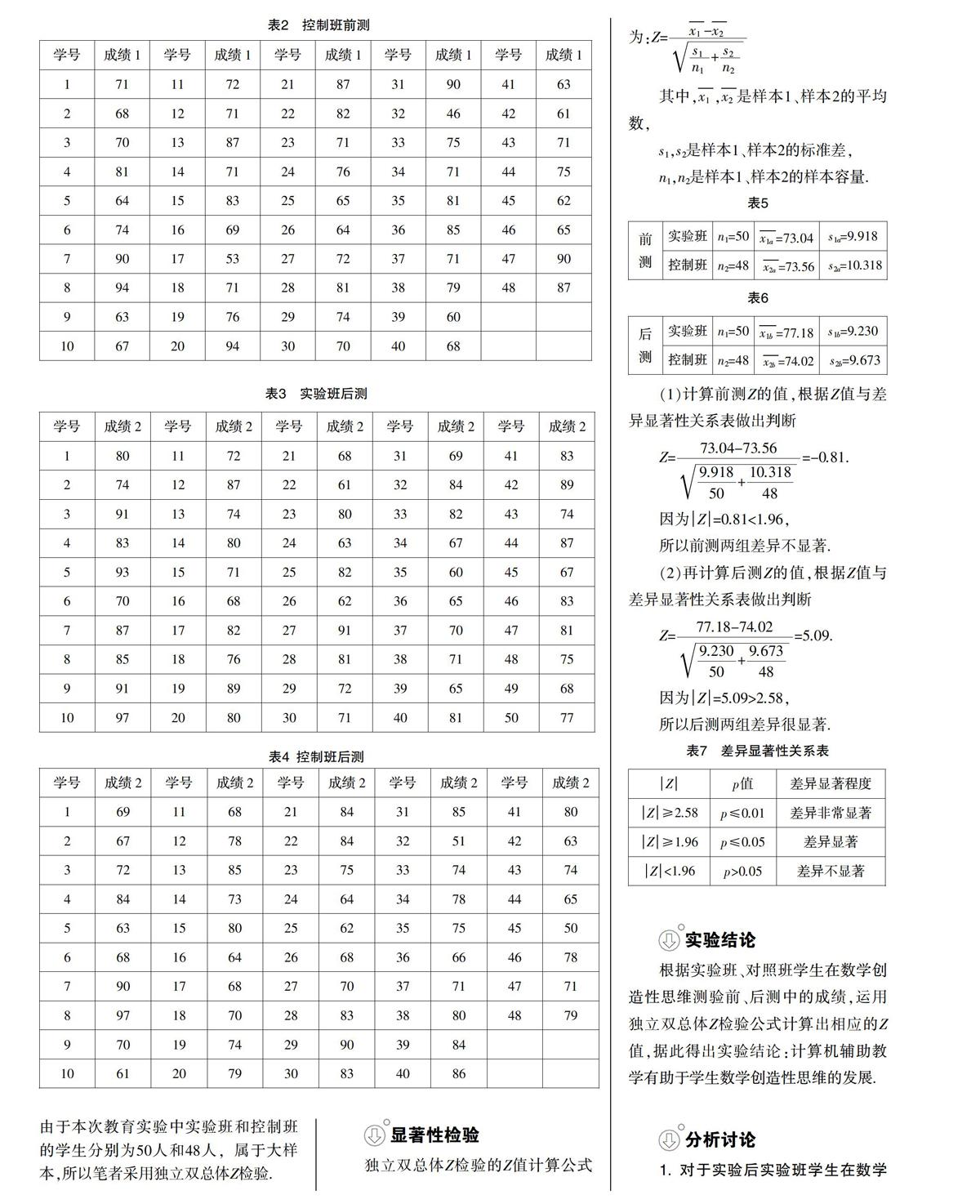
筆者于9月4、5、6三天對實驗班及控制班學生分別進行了《數學創(chuàng)造性思維測驗》的前測. 其原始數據見表1、2.

之后對實驗班學生導入實驗因子.本實驗中計算機輔助數學教學主要應用的軟件是平臺型工具軟件“幾何畫板”.

筆者于11月5日對實驗班及控制班學生分別施以《數學創(chuàng)造性思維測驗》的后測. 其原始數據見表3、4.

最后對兩組數據進行顯著性檢驗.由于本次教育實驗中實驗班和控制班的學生分別為50人和48人，屬于大樣本，所以筆者采用獨立雙總體Z檢驗.

實驗結論

根據實驗班、對照班學生在數學創(chuàng)造性思維測驗前、后測中的成績，運用獨立雙總體Z檢驗公式計算出相應的Z值，據此得出實驗結論：計算機輔助教學有助于學生數學創(chuàng)造性思維的發(fā)展.

分析討論

1. 對于實驗后實驗班學生在數學創(chuàng)造性思維測驗中成績顯著提高的原因分析

根據對本教學實驗有關數據的分析，在實驗后，實驗班學生在數學創(chuàng)造性思維測驗上成績顯著高于對照班學生，筆者認為導致這一結果的可能原因有以下幾點：

（1）計算機輔助教學的直觀形象性為學生的形象思維提供了豐富的素材，有助于數學模型在學生頭腦中的構建，從而為創(chuàng)造想象和直覺思維的發(fā)展提供了條件.

多媒體計算機的高速運算功能和位圖模擬功能，能夠將復雜的數學變化過程瞬間模擬完成，并將其運動過程及函數圖象顯示于屏幕之上，使學生能對難以掌握的、多變的運動中間暫態(tài)過程及函數曲線一目了然.

計算機輔助教學的直觀形象性，不僅有利于學生形象思維的發(fā)展，也為學生的邏輯思維提供了鮮活的材料. 學生可以分析，小球之所以這樣運動、形成這一軌跡，其原因何在？如果改變其中一種或幾種條件，其軌跡又將如何？在學生假想、驗證的過程中，其直覺思維、創(chuàng)造想象以及邏輯思維均得到發(fā)展. 從某種意義上說，學生利用這一教學軟件自主地去研究，對于學生數學直覺思維的發(fā)展及探索精神的養(yǎng)成，遠比教師講解更為有效.

（2）學生利用工具型軟件解決學科具體問題的過程本身就是一種創(chuàng)造性勞動，其思維結果具有創(chuàng)造性.

《幾何畫板》屬于工具型軟件，是高中數學課堂中常用的輔助軟件. 例如，作一條已知線段AG的N等分點（N為自然數，比如為6）. 傳統(tǒng)的作法是過點A作一條射線，在這條射線上用圓規(guī)以A為端點以任意長度截取六條等長線段，AB1，B1C1，C1D1，D1E1，E1F1，F1G1. 然后連接GG1. 分別過B1，C1，D1，E1，F1五個點作GG1的平行線，交線段AG于B，C，D，E，F五點. 可以證明這五點將線段AG六等分，B點為線段AG的六等分點. 若想繼續(xù)作線段AG的五等分點、四等分點、三等分點、二等分點，可依法炮制.

在常規(guī)教學中，除這一作法外，尚無其他可行作法.然而在本次教育實驗中，有一個小組的學生利用《幾何畫板》發(fā)現了另一種作法：仍然是作已知線段AG的六等分點，在《幾何畫板》中畫線段AG（長6 cm），以A為端點作AG的垂線段AA1，再以AA1和AG為兩鄰邊作一矩形A1AGG1. 連接這一矩形的兩條對角線交于點F1，過F1作AG的垂線交AG于點F，利用《幾何畫板》的度量工具可知，AF為AG的. 連接A1F交AG1于點E1，過E1作AG的垂線交AG于點E，利用《幾何畫板》的度量工具可知，AE為AG的.連接A1E交AG1于點D1，過D1作AG的垂線交AG于點D，利用《幾何畫板》的度量工具可知，AD為AG的. 以此類推，可以分別找到點C、點B.

用這種方法可以找到任意已知線段的N等分點，但欲進行幾何證明則相當困難，因而在目前的中學教材中尚無這種作法的先例. 而該組學生通過創(chuàng)造想象和直覺思維，利用《幾何畫板》的度量功能，發(fā)現了這一作法. 類似的例子在本次教育實驗中并不少見. 由此可見，這類工具型軟件為學生們提供了更為廣闊的思維空間，使得他們的許多想象乃至一些異想天開的想法能夠在一個虛擬的世界里得到驗證. 碰壁，會迫使他們去做更加縝密的邏輯思考. 在這種發(fā)現問題、提出假設、檢驗假設、發(fā)現新問題、提出新假設、再檢驗直至解決問題的過程中，學生的創(chuàng)造性思維得到發(fā)展.

（3）計算機輔助教學將以往對數學問題的靜態(tài)研究轉變?yōu)閯討B(tài)研究，學生更容易掌握問題的本質，有利于學生空間想象能力、邏輯思維能力以及辯證思維能力的發(fā)展.

幾何學研究的精髓在于對空間內點、線、面關系的研究. 比如，點運動成線，線運動成面，面運動成體. 一條圓弧，繞不同的軸旋轉，所成的“體”是千變萬化的，憑一塊黑板、一支粉筆，教師很難給學生一個形象、具體的答案. 而利用《幾何畫板》，學生可以隨心所欲地設定圓弧的形狀，選取旋轉軸，觀察旋轉所成的體.當然，這只是極為簡單的例子，對于一些更為復雜的空間點、線、面關系的解析，《幾何畫板》更能顯示其強大的功能. 學生在這個特殊的幾何實驗室內可以通過拖動點、線，旋轉面，去研究它們之間相互關系的本質，這對于學生空間想象能力、邏輯思維能力以及辯證思維能力的培養(yǎng)意義重大.

2. 關于本教育實驗的兩點思考

（1）對于促進學生創(chuàng)造性思維發(fā)展起決定性作用的，并非是以多媒體計算機為代表的現代教育技術本身，而是具有創(chuàng)造性人格特征的教師對這些技術的創(chuàng)造性應用.

（2）技術不是萬能的，計算機輔助教學存在局限性. 如前所述，計算機輔助教學具有傳統(tǒng)的教學手段無法比擬的優(yōu)越性，諸如，能夠對肉眼觀測不到的微觀、宏觀現象進行形象、逼真的模擬，能夠演示理想狀態(tài)下物體的運動過程及中間暫態(tài)，能夠將靜止、孤立的點、線、面進行動態(tài)研究，等等. 然而，虛擬的終歸是虛擬的. 技術本身為學生研究、探索提供了條件，他們可以憑借技術在一個虛擬的世界里，使某個問題簡單化、絕對化，甚至可能是荒唐的；但他們最終需要從這個虛擬的世界里走出來，去面對復雜的、變化著的真實環(huán)境，去解決真實世界里的現實問題.

因此，計算機輔助教學盡管有著傳統(tǒng)教學手段無法比擬的優(yōu)越性，卻不可能完全取代傳統(tǒng)的教學手段. 二者需要有機結合，才能相得益彰，更好地促進學生的發(fā)展.